基于无率码的信息与能量同传中继信道传输速率的优化与实现

雷维嘉，董明昊

（重庆邮电大学通信与信息工程学院，重庆 400065）

1 引言

无线通信网络中，一些节点由于地理条件、工作环境等的影响，电力供应受到限制。从环境中收集能量是解决供电受限通信系统能量供应的重要手段，近年来，提出的无线信息与能量同时传输（SWIPT, simultaneous wireless information and power transfer）技术是一种解决方案[1]。SWIPT是指在无线传输中通过射频信号同时传输信息和能量，节点在接收信息的同时，收集射频信号中的能量转换为电能，作为设备的一个能源。SWIPT技术主要有时间切换（TS, time switching）和功率分裂（PS,power splitting）2种工作模式[1]。TS模式的接收机将接收的射频信号分时用于能量收集和信号处理，PS模式的接收机则是将接收到的射频信号通过功分器分裂为两部分，分别用于能量收集和信号处理。当通信的收发端之间距离过长，或由于障碍物的遮挡，直接传输信号损耗很大时，在收发设备间设置中继节点进行转发，可提高信号的传输质量。中继系统中，中继节点可能会放置在电网没有覆盖的地方，电池的更换也可能不方便。中继节点采用SWIPT工作模式，从接收到的射频信号中收集能量，用于信号的转发，是解决中继节点能量供应的一种手段[2]。

很多文献对SWIPT协作中继方案进行了研究。文献[3]研究了无线传感器网络中的 SWIPT协作中继方案，网络中的节点可工作在能量收集和信息接收模式下。该文献对网络的能量效率进行优化，给出了无冲突调度的初始化算法，并通过数学变换求解优化问题，给出了能量效率最大化的资源分配策略。文献[4]研究了源与目的端间同时存在直连链路和功率分裂 SWIPT中继链路时系统的中断性能，给出了高信噪比下的中断概率闭式解，在此基础上推导了SWIPT最优功率分裂因子的表达式。文献[5]研究了双向SWIPT中继网络中PS模式中继的译码转发（DF, decode-and-forward）协议，提出了完成双向信息交换的三步方案，并推导了中断概率和吞吐量的解析表达式。文献[6]研究了功率分裂SWIPT中继网络中，完美与不完美信道状态信息（CSI,channel state information）下功率分裂因子的优化问题，研究中采用了更能反映实际电路特性的非线性能量收集模型，推导了最优的功率分裂因子的表达式。文献[7]给出了在对数正态分布衰落信道下，SWIPT中继网络中采用DF中继协议，SWIPT分别为理想模式、PS模式和TS模式下中断概率的解析表达式，并通过仿真表明优化能量收集时间和功率分裂因子可以提升系统性能。文献[8]研究了能量收集中继网络中功率分裂和时间分配（TA, time allocation）的联合优化问题，推导了中断概率与中断容量的解析表达式，并在此基础上求解最优TA因子和PS因子，根据瞬时CSI，分步迭代求解联合优化问题。仿真结果证明，对时间分配和功率分裂联合优化可以获得系统中断性能增益。文献[9]研究了三节点中继系统中存在直连链路时，理想模式、PS模式和TS模式这3种中继SWIPT接收模式下信息传输速率的优化问题，并提出可通过无率编码来实现信息与能量的同时传输。传统码率固定的编码方案在信道状态发生变化时，需要根据CSI选择不同码率的编码以适应信道。无率码的码率灵活，可以结合不同的调制方式适应变化的信道质量，能很好地适应 SWIPT中继系统中功率分裂因子或时间切换因子变化导致的信道容量变化。

本文对第一跳采用PS模式的SWIPT中继传输系统的性能优化进行研究，在中继采用DF协议条件下进行功率分裂因子的优化。与现有方案的不同之处在于，本文采用两跳传输时长不等的时隙分配方案，在给定传输信息量的条件下，以最小化系统两跳传输的总时间为目标对 SWIPT的功率分裂因子进行优化。在获得优化的功率分裂因子的基础上，利用无率码的码率可变特性，结合不同的调制方式，适应两跳传输时不同的信道容量，以逼近信道容量的速率实现信息高效而可靠的传输。文献[9]也研究了采用无率码的 SWIPT中继方案，但仅进行了系统性能的仿真，并未给出无率码的码率和调制方式的选择机制。本文则在功率分裂因子优化的基础上，给出了采用Raptor码时调制方式、译码器译码码字长度（即码率）的选择机制。

2 系统模型和功率分裂因子的优化

本文研究的是由源节点 s、半双工中继节点 r和目的节点d组成的三节点两跳中继模型，中继采用DF模式进行转发，如图1所示。设系统两跳的传输距离分别为D1和D2，路径损耗因子为c，s到r、r到 d的路径损耗分别表示为和。小尺度衰落为瑞利衰落，两跳的小尺度衰落因子分别记为α1和α2，为均值为0且单位方差为1的复高斯分布的随机变量。系统两跳的信道系数分别为

图1 系统模型

传输的第一跳采用 SWIPT方式，且中继采用功率分裂模式，传输时隙如图2所示。一次传输分为2个阶段，第一阶段为传输的第一跳，源节点发送信号，中继处对接收信号进行功率分裂，分成信息信号和能量信号两部分。信息信号送入译码器进行译码，能量信号则进入能量收集设备转换为能量并存储。第二阶段为传输的第二跳，中继对译码得到的信息重新进行编码，并用第一阶段收集的能量发送。系统两跳的时间长度可以不相等，与瞬时的信道质量、源节点的发送功率和中继的功率分配因子有关。

图2 功率分裂模式下的时间分配

记源节点的发送信号为xs，具有单位功率。中继节点处的接收信号为

其中，Ps为源节点信号发送功率，nr为中继节点接收到的信道噪声，服从均值为0且方差为的复高斯分布。中继节点对接收信号进行分裂，分裂为信息信号yrI和能量信号yrE两部分。进入译码器的信息信号为

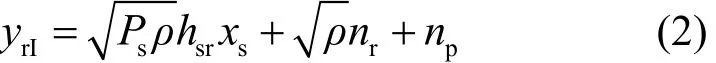
其中，ρ为功率分裂因子，即分裂后信息信号功率与接收信号总功率的比值；np为中继节点信号处理电路产生的复高斯噪声，其均值为0，方差为。能量信号为

中继通过信息信号进行信息译码，信息信号信噪比（SNR, signal-noise ratio）为

第一跳源节点与中继节点间的信道容量为

其中，B为信道带宽。若一次传输的总信息量为I，以该信道容量进行传输，第一跳的传输时长为

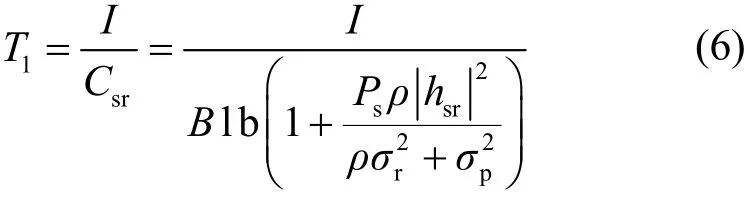
中继将能量信号yrE转换为电能存储，第一跳中收集到的能量为

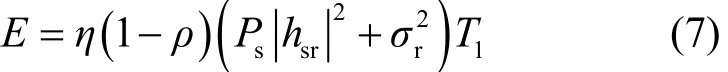
其中，η为能量转换效率。

第二阶段，中继节点对译出的信息重新编码后转发。设转发信号为xr，满足单位功率约束。设第二阶段的传输时长为T2，在收集能量的约束下，中继节点的信号转发功率为

目的节点接收到的信号为

其中，nd为目的节点的复高斯白噪声，其均值为0，方差为。目的节点的接收信噪比为

中继节点与目的节点间的信道容量为

第二跳传输所需要的时间为

总的传输时长为

PS模式下两跳的传输时间都与功率分裂因子ρ有关。ρ越大，中继处分裂出信息译码的信号功率越大，信噪比越高，第一阶段传输时间越短；但用于能量收集的信号功率就越小，同时收集能量的时间也越短，收集的能量就越少，导致第二跳时中继转发功率越低，第二阶段的传输时间越大。反之ρ越小，第一阶段传输时长越大，而第二阶段的传输时长越短。因此，总的传输时间是ρ的非单调函数，优化它可得到最短的传输时间。优化问题可表述为

观察T2的表达式(12)可以看到，等号的两侧都有T2，并不能将其转化为一个明确的关于ρ的函数，因此无法通过解析求解的方式得到最优功率分裂因子的解。由于ρ∈(0,1)，取值范围有限，可采用搜索的方法来求解优化问题，如采用黄金分割法。限于篇幅，这里不对黄金分割法进行介绍。采用黄金分割法求解的过程中，需要多次迭代求解分割点ρ值下的传输时长。给定一个ρ值时，将其代入式(6)进行简单的计算可得到相应的T1，但将其代入式(12)后却不能直接求得T2的值，下面给出T2的求解方法。

将式(12)中的T1用式(6)代换，并转换为

可以简写为

T2的求解问题就是求解方程的根，获得使式(16)成立的解。式(16)为超阶方程，为求解该方程，下面先给出引理1。

引理 1形如的超阶指数方程的解为，其中W(⋅)是朗伯W函数[10]。该方程解的证明详见文献[11]。

由引理1求解式(17)，得到x，再经过转换就可得到给定ρ值下第2跳传输时长，如式(18)所示。

3 无率码码长和调制方式的选择

无率码最初作为纠删码应用于二进制删除信道[12]，但也可用于高斯噪声信道[13]。对于给定的信息长度，无率码编码器产生的编码符号长度不固定，其码率由译码器根据译码所需要的编码符号数决定，因此码率是可变的。由于无率码具有码率可变特性和译码时的互信息累积特性，在时变的信道容量下，利用无率码仍可实现高效而可靠的信息传输。Raptor码[14]是一种级联结构、性能优良的无率码，其外码是高码率的低密度奇偶校验（LDPC,low-density parity-check）码，内码是 LT（Luby transform）码，编码过程包括预编码和 LT编码两步。Raptor码译码时先在内层用 BP（belief propagation）译码算法进行 LT码的译码，再在外层进行LDPC码的译码。LT码的BP译码是软判决译码，译码器输入为接收比特符号的似然比软信息。LT码的迭代译码过程完成后输出中间编码比特的软信息，送入LDPC码的译码器进行LDPC译码。

在衰落信道下，接收端接收到的信号为

其中，x为单位功率信号，h为信道系数，n为均值为0、方差为2σ的复高斯白噪声。对接收信号进行简单的变换，得到

为适应传输质量变化的信道，本文采用码率可变的Raptor码结合不同的调制方式，实现高效和可靠的信息传输。采用5种调制方式，包括二进制相移键控（BPSK, binary phase shift keying）、正交相移键控（QPSK, quadrature phase shift keying）、16阶、64阶和256阶的正交幅度调制（QAM, quad-rature amplitude modulation）。当信道衰减变化范围更宽时，增加更高阶调制即可。对于M阶调制，每个符号中的比特数为lbM。接收符号r中的第ibitbi的对数似然比（LLR, log-likelihood ratio）为

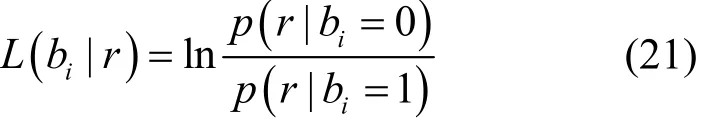
其中，p(.)表示概率密度函数（PDF, probability density function）。

接收端要成功译码必须累积足够的互信息量。接收符号r与发送符号x的互信息为

其中，信息熵h(r)的计算式为

在先验等概的条件下，采用M阶调制时，各符号的发送概率为。条件熵h(r|x)的计算式为

采用M阶调制时，要达到期望的译码误码性能，译码器对一个码字进行译码时需要的互信息总量为IM，则发送的符号数为

Raptor码是一种随机编码，没有编码结构，不能从理论上分析其误码性能。为了在译码时得到码字的长度，可先采用仿真的方式获得固定码字长度下达到要求的误码性能时对应的信噪比，然后换算为互信息量要求，最后确定码字长度。为此在加性高斯白噪声（AWGN, additive white Gaussian noise）信道上对 Raptor码进行仿真。本文采用的 Raptor码外码为R= 0.95的LDPC码，输入信息长度K=9 500 bit，中间编码信息长度m=10 000 bit。LT码的编码度分布为[14]

本文以误字率（WER, word error rate）来评价差错性能。图3给出了采用不同调制下，Raptor码译码码字长度为19 000 bit时误字率的仿真结果。根据仿真结果，估计出5种调制方式在达到WER =10-3的差错性能时需要的信噪比，然后根据式(22)～式(26)计算出该信噪比下的符号互信息量，最后乘以符号数（即）就得到译码需要的互信息总量IM，如表1所示。

图3 AWGN信道下码字长度为19 000 bit时Raptor码的误字率

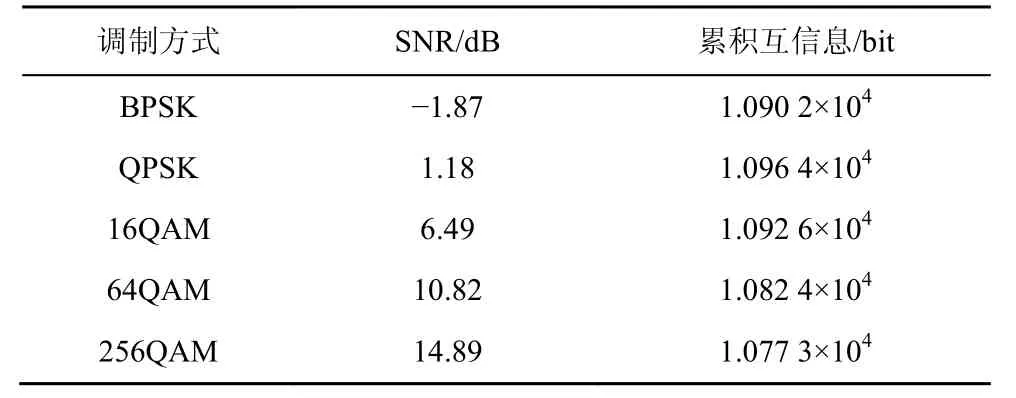
表1 5种调制方式下WER = 10-3时的信噪比和译码所需累积的互信息

由于译码复杂度与译码码字长度成正比，为了控制译码复杂度，需要限制其长度。为了能以逼近信道容量的速率传输信息，应尽量选择高阶调制，获得更高的传输效率。但高阶调制下由于一个符号携带多个比特，在同一信噪比下，虽然符号互信息较低阶调制符号高，但平均每个比特互信息较少，译码时需要更多的比特，即译码码字长度更长，译码复杂度更高，故选择调制方式时应同时考虑传输效率和译码复杂度。本文方案设计时限制译码码字长度不超过21 100 bit。表2中以1 dB为间隔给出了信噪比在-2 ～25 dB范围内注1注1 受篇幅限制，文中给出以1 dB为间隔的表格，实际应用时可根据需要按更小的信噪比间隔制作表格，如0.1 dB，与信道的匹配程度更高。本文仿真部分采用0.1 dB为间隔的表格。，5种调制方式的符号互信息量，以及在达到WER = 10-3的差错性能要求时，传输一个码字的9 500 bit的信息时需要发送的比特数（即译码器对一个码字进行译码时码字的长度），相应的符号数可用比特数除以 lbM得到。表2中用黑体标识的是根据上述准则选择的调制方式下，平均符号互信息量和译码码字比特数。通信过程中，根据接收端的瞬时信噪比选择调制方式，选择原则是在译码码字比特数不超过最大值的条件下，选择符号互信息最大的调制方式，如式(30)所示。

优化后的中继系统中采用 Raptor码进行编码传输时，中继处采用译码转发协议，先对接收信号进行译码，再重新编码。由于两跳的信道容量不同，因此源和中继处各自选择合适的调制方式。第一跳，首先将求解得到的最优功率分裂因子ρ代入式(4)中得到中继处信息信号的瞬时信噪比，通过查表 2得到调制方式和一个码字的长度，进一步计算得到对应的发送符号数。对于第二跳，则由式(10)得到目的端接收信号瞬时信噪比，然后根据表2得到调制方式和码字长度，并计算得到发送符号数。

4 仿真

为了验证本文优化方案的性能，将 PS模式下的两跳等时长 DF方案、放大转发（AF, amplifyand-forward）方案与本文所提的优化方案进行仿真对比。等时长DF方案两跳的传输时长相同，选择功率分裂因子ρ的值使两跳的信道容量相同，即两跳的接收信噪比相同。记经过分析，得到两跳等时长DF方案功率分裂因子的最优值为

其中，将ρ∉(0, 1)的值舍去。在AF方案下，应使目的端的信道容量最大，此时传输时间最短。记J=经分析得到AF方案下最优的功率分裂因子为

其中，将ρ∉(0, 1)的值舍去。

4.1 以信道容量的速率进行传输的仿真

在下面仿真中，设定传输信息量I= 9 500 bit；能量转换效率；路径损耗因子c= 3；信道带宽B=1 MHz；源节点s和目的节点d之间的距离保持60 m不变，即d1+d2= 60 m。两跳信道的小尺度衰落因子α1、α2为相互独立的复高斯随机变量，均值为0，方差为 1。传输时长和吞吐量的结果是 4×106个信道样本下仿真实验结果的平均值。为简便起见，仿真图形中将两跳等时长DF方案、AF方案和本文提出的两跳不等时长 DF方案分别简记为DF、AF和ueDF。

改变中继节点在s—d连线间的位置，源节点发送功率设置为-2 dBm，对本文提出的优化方案与2种对比方案在以信道容量的速率传输9 500 bit的信息需要的时间进行仿真，仿真结果如图4所示。仿真结果显示，3种方案都是中继节点位于源节点和目的节点中间时性能最差，靠近源节点或目的节点时性能较好。由于中继节点转发信号所需能量从源端发送信号中收集，中继节点越靠近源节点，在保证第一跳传输速率的前提下，可以分裂更多的信号功率用于能量收集，收集到更多的能量，提升第二跳的转发功率；当中继节点靠近目的节点时，第二跳路径损耗较小，转发需要的功率较小。因此中继节点靠近源节点或目的节点时 SWIPT中继系统传输性能较好。这与常规供电的中继系统不同，常规供电的中继系统中，中继节点位于源节点和目的节点的中间附近时性能最好。这也说明，当源节点与中继节点间存在障碍物遮挡不能直接通信，需要由SWIPT中继节点进行转发时，应当在地理条件允许的情况下，尽量将中继节点靠近源节点，或靠近目的节点放置。2种对比方案中，两跳等时长DF的性能要优于AF，而本文的ueDF方案的性能最优。相比较 AF，本文方案的传输时间缩短了约 50%，较DF则缩短了约30%。显然，采用两跳不等时长的安排可以获得更好的性能。

表2 不同信噪比时5种调制方式的符号互信息量和一个码字的长度

设置d1= 45 m，d2= 15 m，不同源节点发送功率时，3种方案传输时间的仿真结果如图 5所示，3种方案的吞吐量（单位时间、单位带宽内传输的数据量）如图6所示。仿真结果显示，随发送功率增加，3种方案的传输时长缩短，而吞吐量增加。与图 4的结果类似，两跳等时长 DF的性能较AF更优，而ueDF的性能最佳，需要的传输时间最短。在源节点发送功率为-2 dBm时，相比两跳等时长 DF系统，本文方案吞吐量高约30%，比 AF系统则高约 50%。说明两跳不等时长的安排，可通过优化第一跳中的功率分裂因子，在两跳间更好地分配传输时间，最大限度地利用有限的能量传输最多的信息。

图4 中继不同位置时的系统传输时长 (Ps = -2 dBm)

图5 不同源端发送功率时的系统传输时长

4.2 采用Raptor码的仿真

4.1节给出了中继以优化的功率分裂因子对接收信号进行功率分裂，然后以信道容量的极限速率进行信息传输的仿真结果。本节将给出采用第3节介绍的方案，根据优化功率分裂因子条件下的瞬时信道信噪比，选择适当的Raptor码的码字长度和调制方式进行信息传输的仿真结果。一个信息组仍然为一个码字的信息长度I= 9 500 bit。中继靠近目的端放置，d1= 45 m，d2= 15 m。信道系数在一个码字的传输中保持不变，在码字间改变。其他仿真条件与4.1节相同。

图6 不同源端发送功率时的系统吞吐量

首先对差错性能进行仿真。表3给出了以误字率WER = 10-3为目标时，105个信息组在两跳传输中的误字率。为更清楚地观察误字率的变化情况，将仿真结果在图7中绘出。从图7可以看到，误字率都在期望目标附近波动，偏差很小，说明Raptor码的码字长度和调制方式的选择是正确的。

表3 不同发送功率下采用Raptor码时两跳的误字率

图7 不同功率下采用Raptor编码时两跳传输的误字率

图8给出了本文优化方案和2种对比方案采用第3节给出的编码和调制选择机制，传输9 500 bit的信息需要的时间，同时也给出了以信道容量的极限速率进行传输所需的时间对比。从图8可以看到，3种方案实际需要的传输时间与理论极限值的变化趋势一致。本文方案所需要的时间低于2种等时长方案所需要的时间，再次证明本文采用两跳不等时长的安排具有更好的性能。采用Raptor码和不同阶数的调制方式组合进行传输时所需要的时间稍高于理论极限值，但差距不大，说明本文的速率适应方案能较好地逼近信道容量，信道编码的性能较好。图9给出了3种方案的吞吐量的仿真结果，与图8的结果类似，实际实现的吞吐量稍低于理论极限值。

图8 不同发送功率时3种方案的传输时间

图9 不同发送功率时3种方案的吞吐量

5 结束语

本文对采用功率分裂模式的 SWIPT中继信道传输速率的优化方案进行研究。信息传输分为2个阶段，第一阶段源节点向中继节点发送承载信息的信号，该信号同时也是中继转发能量的来源。中继将接收到的信号分裂成信息信号和能量信号两部分，能量信号转换为电能用于第二阶段的信号转发，而信息信号则用于信息译码。与其他研究类似问题的文献相比，本文的方案中两跳传输时长可不相等。在传输信息量一定时，以最小化两跳总传输时间为目标对功率分裂因子进行优化，采用数值计算结合朗伯W函数求解超阶方程的方法求解最优功率分裂因子ρ。与等时长的DF方案及AF方案的仿真对比表明，两跳不等时长的时间分配可以获得更好的传输性能。但两跳不等时长的DF方案在求取最优功率分配因子时不能得到解析计算式，必须采用数值计算的方法得到，计算复杂度较高。数值计算中可采用黄金分割法、二分法等降低计算复杂度。进一步，研究了采用Raptor码结合不同调制方式，在两跳不同信道容量下，实现高效而可靠的信息传输的机制。通过互信息分析，给出了在一定差错性能要求下调制方式、Raptor码长的选择机制，并通过仿真对所给出机制的性能进行了验证。仿真结果显示，采用给出的Raptor码方案可在达到系统差错性能要求的条件下，以逼近信道容量的速率进行信息传输。