装配式空心板梁桥铰缝数值分析与试验研究

黄卫国，俞博，易汉斌

(1.江西省公路工程检测中心，江西 南昌 330100；2.江西省长大桥隧研究设计院有限公司)

1 前言

装配式空心板梁桥通过空心板间的铰接构造传递板间的竖向剪力，并主要通过该剪力实现行车荷载的横向传递与分配。由于构造和施工等问题，铰缝始终是空心板梁桥的薄弱环节，当其强度不足以抵抗行车荷载产生的竖向剪力时，铰缝混凝土在行车荷载作用下就会开裂。目前，当装配式混凝土空心板梁桥竣工验收或出现病害时，往往用铰接板法横向分布计算值和实测值进行比较，以此来评定是否达到设计要求或需要维修加固。值得注意的是，铰接板法简单地把铰缝简化成只传递剪力、不传递弯矩的铰，是在空心板梁桥设计时采用的方法，重点是解决板的设计，而非铰缝，很难直接地、有效地用于衡量铰缝的抗剪性能。美国Huckelbridge等提出用相对位移差来评价铰缝的抗剪性能，并进行了实桥荷载试验，实测表明，某些铰缝相对位移差最大达到0.5 mm，这足以直接说明该铰缝已经发生损伤。铰缝是板之间的局部传力区域，可以说，相对位移差反映了铰缝剪切受力状态的直接量。铰缝的局部受力分析多采用Ansys、Abaqus等商用有限元软件来完成。由于空心板和铰缝的几何尺寸相差过大，采用实体单元建模会导致单元过多，计算代价较大；且直接得到局部应力而非内力，无法很好地用于分析铰缝的横向剪切性能。目前有关装配式混凝土空心板梁桥铰缝的模拟的研究成果相对较少。

为此，该文结合空心板梁桥结构形式和受力特点，引入有限条元计算理论，利用有限条元模拟空心板和铰缝，并用铰缝相对位移差来衡量铰缝的横向剪切性能，为铰缝横向抗剪性能提供有效的数值分析方法，并通过装配式空心板梁桥实桥荷载试验进行验证。

2 有限条法及控制方程

装配式空心板梁桥在纵向是一典型的条带结构，用有限条元模拟是适合的。在直角坐标系下，有限条元的应变与位移关系为：

(1)

有限条元(图1)位移插值函数为：

(2)

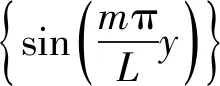
图1 有限条元

有限条元刚度矩阵为：

(3)

式中：D为弹性矩阵;应变矩阵B由式(2)代入式(1)推求。式(3)中：

(4)

利用谐函数Ym=sin(Kmy)的正交性，式(3)成为主对角块阵：

Ke=diag[Ke11Ke22…Kerr]

(5)

则装配式空心板梁桥的第m项有限条控制方程为：

KmmUm=Rm

(6)

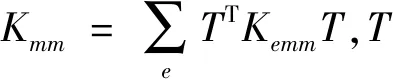
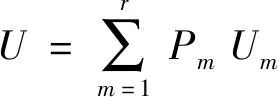
(7)

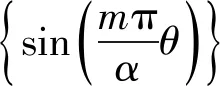
3 空心板梁桥数值模拟及实桥试验

某新建3×20 m装配式预应力混凝土简支空心板梁桥，试验选取了其中一跨。试验桥计算跨径为19.3 m，桥宽为13.5 m，横向由9块中板和2块边板组成，共有10道铰缝，空心板宽1.17 m，高0.9 m(图2)。主梁混凝土为C40。

试验采用两辆加载车进行加载，①加载车前轴单个轮载3.36 t，中、后轴单个轮载5.96 t，总重30.86 t；②加载车前轴单个轮载3.13 t，中、后轴单个轮载5.775 t，总重29.24 t；试验进行了两个工况加载，对应加载车尺寸及作用位置如图3所示。

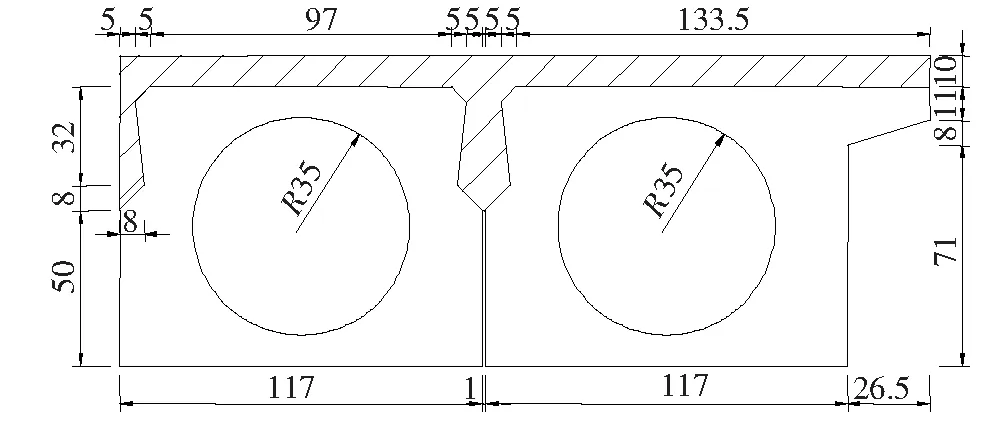
图2 试验桥空心板及铰缝(单位:cm)

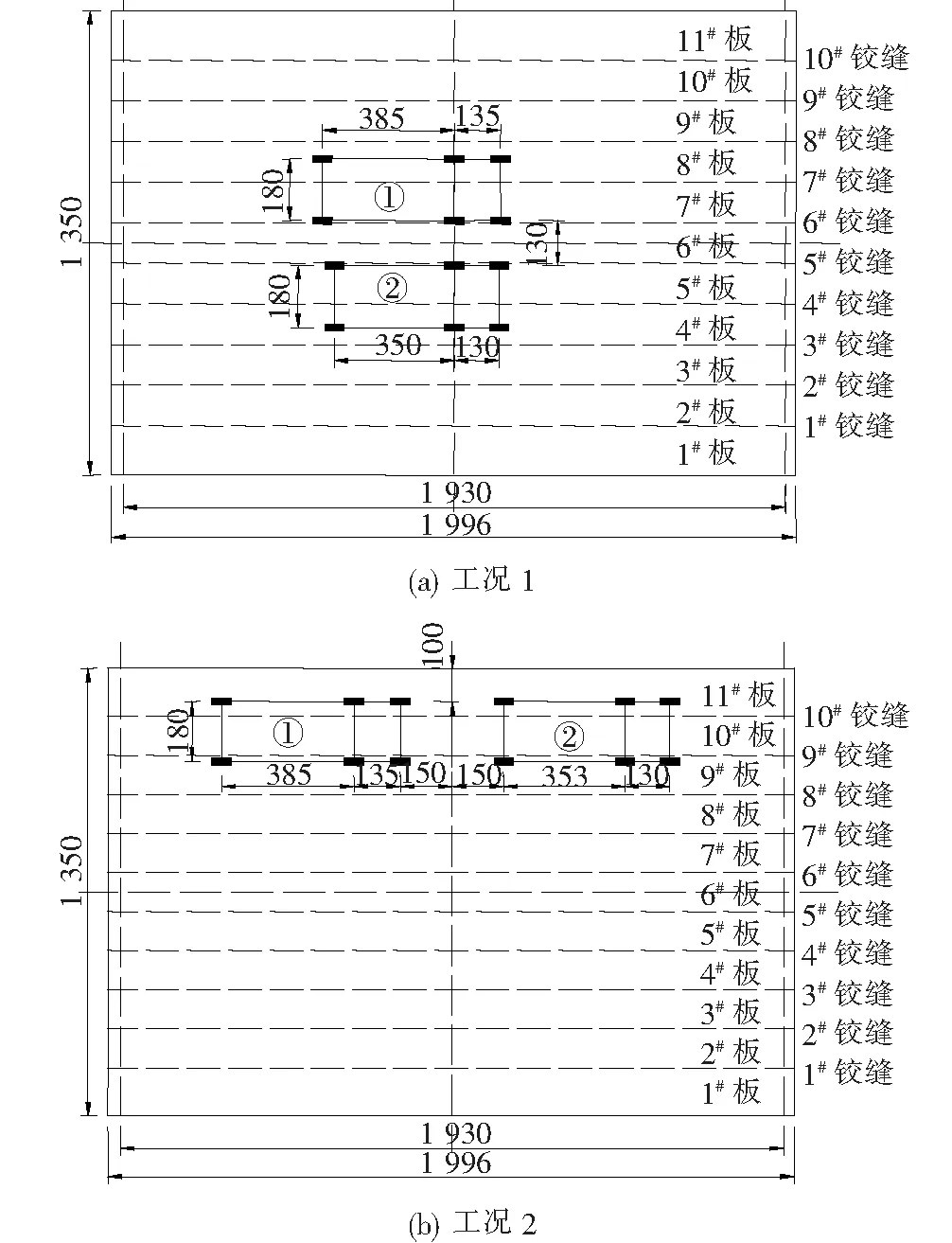
图3 加载工况(单位:cm)

根据有限条控制方程编写有限条的计算程序。装配式空心板梁桥在纵向是一典型的条带结构，根据试验桥空心板和铰缝的几何尺寸和材料特性，横向划分为21个条带，其中空心板11条、铰缝10条。空心板单元编号见图4。

图4 空心板的单元编号

在计算模型中，混凝土材料等级为C40，取弹性模量E=3.25×104MPa，剪切模量G=E/2.3。空心板条元和铰缝条元各向刚度计算值如下：

对于板条元，纵向弯曲刚度Dy=2.23×109N·m，横向弯曲刚度Dx=1.59×109N·m，扭转刚Dxy=3.60×108N·m；假定铰缝完好，高度h为0.5 m，铰缝条元的横向抗弯刚度为Dx=Eh3/12，其他各向刚度则同板条元。

梁格法的主要思路是将上部结构用一个等效的平面梁格或空间构架来模拟，在处理空心板梁桥时，纵向以板为单位考虑板的抗弯抗扭刚度，横向用虚拟横梁模拟，板间横梁连接(铰缝)只能简化成铰接和刚结两种。该文以加载工况2偏载为例，荷载试验中的横向分布与设计时采用的横向分布系数稍有不同，以每块板跨中横向中点的挠度和为100%，每块板挠度与总挠度之比作为荷载横向分布，图5为空间梁格法模型荷载横向分布计算值和实测值结果。

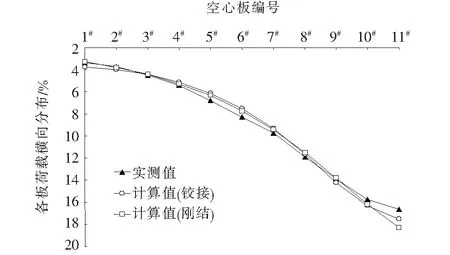
图5 梁格法计算的空心板荷载横向分布比较

由图5可知：空间梁格法模型计算得到的荷载横向分布系数与实测值较为吻合，能够反映主梁的受力。但是，梁格法模型横梁(铰缝)采用铰接和刚结对主梁荷载横向分布影响很小。梁格法的主要问题在于横向联系(铰缝)只能简化成铰接与刚结，很难把铰缝作为一个独立的单元进行考虑。因此，主梁荷载横向分布很难直接用于评价铰缝受力性能，空间梁格法模型也很难模拟铰缝局部受力。

有限条计算模型计算得到各铰缝的相对位移差，并与实桥荷载试验值比较，见表1。表中各铰缝相对位移差是编号小板侧的竖向位移减去编号大板侧的竖向位移，即相对位移正负号代表剪力的传递方向，“+”代表编号小板向编号大板传递，“-”则反之。

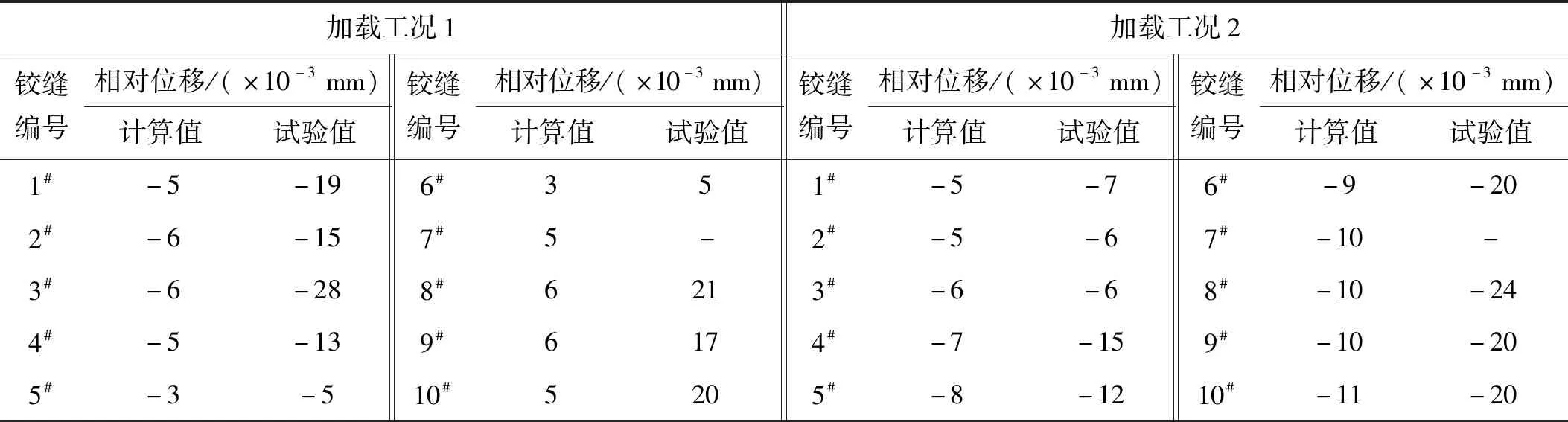
表1 实桥1铰缝相对位移差

由表1可知：有限条程序计算得到铰缝相对位移差为1×10-3～1×10-2mm数量级，这个数量级的变形差是可以通过现有的试验仪器(百分表、千分表等)测得的。实桥荷载试验表明：实测值的数量级与计算值是一致的，但实测值较计算值大，显示铰缝存在一定的损伤。该文采用的有限条法程序中，铰缝作为独立的单元，其属性包括截面特性和材料属性，因此，可以模拟不同的铰缝状态。

4 结语

该文针对装配式空心板梁桥，引入有限条元计算理论，利用有限条元模拟空心板和铰缝，并用铰缝相对位移差来衡量铰缝的横向剪切性能。数值计算及试验结果表明：该文提出的铰缝相对位移差为1×10-3～1×10-2mm数量级，是实际可测的。相比商用软件，有限条计算理论很好地符合了装配式空心板梁桥的条带特点，能用较少单元进行空心板铰缝的横向抗剪性能分析，计算效率高。另外，有限条元法可以把铰缝划分为单独的条带单元，有利于采用优化算法对铰缝损伤进行识别。