连续强降雨工况土质边坡非饱和渗流及稳定性分析
邹文华,刘辉,邓小钊,刘耀坤
(1.长沙理工大学 土木工程学院,湖南 长沙 410114;2.长沙拓正交通科技有限公司;3.湖南理工学院)
降雨是岩土体边坡滑坡失稳的主要因素之一。据统计,暴雨诱发滑坡约占总量的90%。在中国南方地区,降雨强度200~300 mm/d时就容易诱发大型滑坡;已有研究表明:滑坡的发育程度和雨量有关,且滑坡一般发生于久雨、暴雨中或略滞后。降雨过程中渗流场改变了孔隙水压力进而影响了土体的有效应力,导致土体骨架的变形。因此,考虑降雨渗流会对边坡稳定性造成影响,部分学者建立起边坡降雨渗流与边坡稳定性的关系。
Fredlund等在非饱和土抗剪强度理论中,指出土体孔隙水压力增加会引起抗剪强度降低;同时,降雨入渗会引起边坡土体体积含水率上升,造成边坡土体重度增加,导致下滑力增加,从而引起边坡稳定性下降。Collins等和Johnson等通过分析实例分别得到边坡土体雨水渗入速率对边坡失稳有着重要影响的观点,渗入速率较快时边坡出现失稳的深度较浅;渗入速率较低时,边坡出现失稳深度较深;王一兆等通过分析浅层滑动面在不同降雨时段的渗透系数和孔隙水压力,得出边坡在浅层滑动面稳定性的变化规律;曾铃等通过饱和非饱和渗流理论与非饱和抗剪强度理论,深入研究了在降雨强度、渗透系数、边坡坡度3个入渗因素对炭质泥岩边坡的稳定性影响;汪丁建等考虑湿润锋以上饱和带渗流作用,指出Green-Ampt模型的不足,同时研究了湿润锋的分布特点,并建立了边坡稳定系数表达式。
以上模拟研究直接或间接考虑了体积含水量对边坡稳定性的影响,但就研究方式而言,仅取边坡的一点或一个面作为研究对象,而岩土体结构复杂多样,边坡不同位置所处的内环境不尽相同,以至于得出的结论难以作为实际工程的依据。该文将从边坡坡顶,坡面以及坡脚的多个位置的进行模拟分析,从实际工程出发得到更加可靠的结论。
1 渗流原理以及抗剪强度分析
达西定律是基于饱和土的渗透分析建立的,达西定律可采用如下公式:
v=ki
(1)
式中:v为渗流速度;k为渗流系数;i为水力梯度。
Richards在1931年通过试验证明了达西定律在非饱和土中的适用性,因此将达西定律扩展至均质材料的非饱和渗流中,同时给出土体渗透系数与其基质吸力有关,但由于获取土水特征曲线的试验技术难度较大,基质吸力的量测相对困难,可利用Van Genuchten模型进行拟合。模型表达式为:
(2)
式中:Θw为体积含水量;Θs为饱和体积含水量;Θr为残余体积含水量;ψ为负孔隙水压力;a、n、m为曲线拟合参数。
在饱和土中,水力渗透系数是常量,而在非饱和土中渗透系数则与基质吸力或体积含水量有关。考虑渗透系数和基质吸力之间的关系:
(3)
式中:kw为渗透系数;α为坡面与水平面的夹角;n=1/(1-m);其他参数意义同前。
在非饱和土中存在基质吸力的作用,太沙基有效应力原理不能直接使用,Bishop引入一个有效应力参数χ来建立非饱和土的抗剪强度公式,基于Mohr-Coulomb强度准则,表达式为:
τf=c′+(σn-μa)tanφ′+χμstanφ′
(4)
式中:τf为膨胀土的抗剪强度;c′为饱和土的有效黏聚力;σn为总正应力;μa为孔隙气压力;φ′为饱和土的有效内摩擦角;μs为基质吸力,μs=μa-μw,μw为孔隙水压力;参数χ的测量试验条件要求高,取值较困难。Oberg等提出了含有饱和度的抗剪强度公式,实际上是将参数χ直接取为饱和度。
Fredlund采用双应力状态变量将Bishop的抗剪强度公式进一步延伸:
τf=c′+(σn-μa)tanφ′+μstanφb
(5)
式中:φb为随基质吸力变化的内摩擦角;其他参数意义同前。
比较式(4)、(5)可以发现:二者都是采用有效黏聚力、基质吸力以及法向应力来描述抗剪强度,其中基质吸力影响的抗剪强度与参数χ和φb有关。
2 降雨入渗特点及模拟方法
2.1 降雨入渗特点
降雨过程中,由于土体内部体积含水量不同,边坡坡面首先达到饱和,形成饱和区;雨水还未到达的区域是非饱和区,饱和区与非饱和区存在过渡区,在该区域的含水率变化较大。湿润锋主要在非饱和区之下。随着降雨不断向边坡内部移动,如图1所示。饱和区逐渐向下移动,随之引起边坡内部的孔隙水压力、含水率上升。
当土体处于非饱和状态时,存在于土体基质吸力使得土体的抗剪强度提高。降雨使得土体饱和度不断增加,导致基质吸力的下降,抗剪强度也随之发生变化,最终导致边坡失稳。在强降雨工况下,边坡浅层基质吸力下降要快很多,更容易失稳,因此边坡渗流的特点与边坡失稳的形式紧密相关,研究边坡土体的渗流特性是评价边坡稳定性的前提。

图1 降雨入渗过程示意
2.2 Geo-studio数值模拟
根据降雨滑坡成因分析,采用Geo-studio中的SEEP/W模块可以有效进行非饱和模拟,首先设置边界条件,假定模型底部为不透水边界,根据SEEP/W模块中的瞬态分析边坡模型两侧的透水边界水头。进入稳态分析,确定边坡孔隙水压力初始条件,随后进入瞬态分析,选择适当的模拟降雨时间区间,根据土体实际渗透系数设置合适的边界条件,当降雨强度大于土体渗透系数时,取土体渗透系数作为边界条件,当降雨强度小于土体渗透系数时,取降雨强度作为边界条件,并根据设好的时间间隔记录降雨过程中的数据变化,随后进入Slope/W模块进行稳定性分析,设置适当滑动面的位置后计算,分析比较边坡安全系数在降雨过程中的变化。
3 工程概况
3.1 边坡模型
为讨论强降雨土质边坡的稳定性影响,该文以衡(阳)-桂(阳)公路某路堑边坡为依托,根据边坡实际情况将模型做一定的简化处理并进行渗流计算以及稳定性分析。根据工程地质资料勘察报告,该区段边坡纵向坡长60~70 m,横向宽50~100 m,坡高28~30 m,在4—5月份受到连续强降雨的影响,坡顶出现贯通的裂缝,垮塌坡体自上向下推移,坡脚处浆砌片石挡土墙已损坏,滑坡体平均厚度约4.8 m,滑坡体体积约20 000 m3,属于小型浅层滑坡,根据钻探结果及现场调查,主要由于持续强降雨渗入残坡积粉质黏土和全风化泥灰岩,渗入的雨水一方面产生较大的孔隙水压力;另一方面使贯通面处的岩土体饱和软化,土体内摩擦角和黏聚力也同时下降,因此诱发了滑坡。该边坡在平行于公路方向上的变化程度不大,因此可以采用二维平面模型进行简化分析,如图2所示。

图2 边坡简化模型(单位:m)
3.2 计算条件
边坡剖面岩层主要有两层,分别为粉质黏土和全风化泥灰岩(土工试验定名为粉质黏土),根据现场勘察试验以及反演值综合确定,边坡参数见表1,土水特征曲线采用Van Genuchten模型对边坡土层进行拟合,拟合结果如图3所示。
中国气象部门采用的雨量划分等级,见表2。该文主要研究强降雨持续作用对边坡稳定性的影响,计算条件根据当地降雨情况,将降雨强度设为200 mm/d的强降雨天气,为了使模拟结果更加清晰,将时间设为连续降雨1个月。

图3 不同土层的土水特征曲线

表1 土层参数

表2 降雨量等级
3.3 降雨过程中孔隙水压力场变化
图4为模拟降雨1个月时间内,边坡各个时间段孔隙水压力等势线分布图。图4(b)、(c)分别为连续降雨5 d和连续降雨10 d孔隙水压力变化,由图4(b)、(c)可以看出边坡坡脚土体孔隙水压力有所提升,负孔隙水压力逐渐降低,土体达到饱和状态,这是由于粉质黏土渗透系数低,渗透速度也低,此时坡面孔隙水压力上升快,使得坡面产生了排水效果,排出去的水抵达坡脚导致坡脚区域的水位首先上升。另外,坡顶全风化泥灰岩区域负孔隙水压力在逐渐减小。
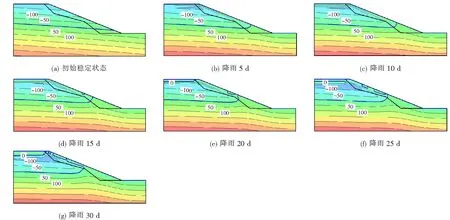
图4 孔隙水压力等势线(单位:kPa)
由图4(d)可知:为降雨15 d后,坡面靠近坡脚处开始出现暂饱和区域,并逐渐向坡体内部移动;降雨20 d后,坡顶处也出现了暂饱和区,负孔隙水压力进一步减小。由图4(f)、(g)可知:随着降雨的继续进行,边坡表层陆续出现零散的暂饱和区,孔隙水压力为-150 kPa的区域完全消失;降雨30 d后,暂饱和区域相互贯通,坡内潜水面向上抬升不明显。
在饱和条件下,土颗粒之间的间隙中充满水,一旦有空气进入其中,土体就成为了非饱和土,空气所在的孔隙就成为非传导的管道,水的渗流也就受到了阻碍,因此渗透系数也随之降低。当负孔隙压力越大,进入的空气也就越多,体积含水量也就相应会减小,渗透系数也就越小。从这一点可解释,由于前期降雨,土体表面的负孔隙水压力较大,体积含水量较低,因此渗透系数低于边坡内部渗透系数,此时坡面的入渗速率也是低于坡内的入渗速率,当受到强降雨作用时,坡面可以很快达到饱和,此时坡面的雨水入渗速率要高于坡内,因此坡内渗流相对受阻,在坡内到坡面一段距离里形成暂饱和区域。另外,由于坡体内部仍存在负孔隙水压力区域,土颗粒中的空气排除路径减少,使得暂饱和区域继续向下扩展的速率减缓,因此形成了饱和区域对非饱和区域的包围之势。
3.4 降雨条件下的稳定性分析
在降雨持续入渗过程中,由于渗流的作用使得孔隙水压力场改变;入渗初始阶段土壤的入渗率较高,基质吸力随入渗率增大而减小,导致土体抗剪强度也在减小,坡体安全系数也就变小,总体呈现负相关,如图5所示。

图5 安全系数随时间的变化情况
边坡稳定性体现在坡体的抗剪强度上,Fredlund提出的式(5)所表达的抗剪强度属于双应力状态变量公式,其中对基质吸力的影响考虑较多。实际上在非饱和土中,由于负孔隙水压力的存在,就会产生基质吸力,且负孔隙水压力越大,基质吸力越大。当土体负孔隙水压力减小时,基质吸力也会不断减小,此时定性地描述负孔隙水压力依旧可以用体积含水量。如图4所示,根据边坡孔隙水压力变化特点,排除坡顶与坡脚的其他因素,选取了坡面中间一系列有代表性的点作为观测点,如图6所示。
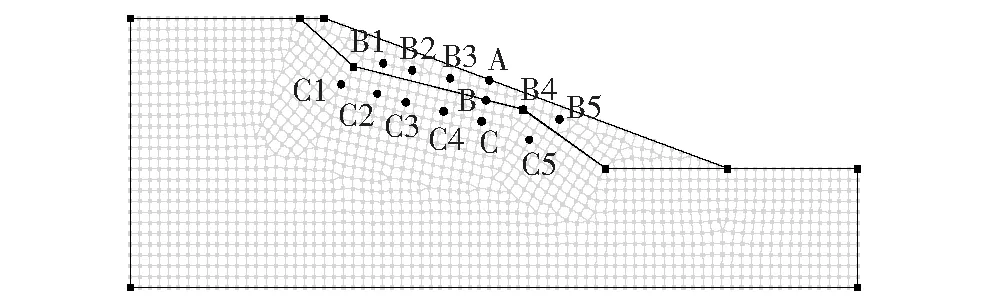
图6 测点位置
图7为观测点A、B、C点的体积含水量与降雨时间的关系曲线,由图7可以看出:测点A边坡坡面体积含水量在降雨初期就达到饱和状态值,这是由于初期坡面负孔隙水压力较大,渗透系数较小从而使得渗透速率较小。测点B为土层交界处在历时20 d左右的强降雨,体积含水量开始增大,并在最后达到饱和,而测点C所在区域的体积含水量增幅很小,可推测B点基质吸力相对于C点要减少得更快。

图7 测点A、B、C的体积含水量变化趋势
实际上,靠近边坡土层交界处区域的体积含水量均有类似于测点B的起伏。选取粉质黏土土层靠近交界处一系列点作为观测对象,如图8所示,B1~B5这些点的体积含水量基本在降雨20 d时产生变化或者已达到最大体积含水量,并且有较大斜率,说明边坡稳定性由此开始变差。相比于取自全风化泥灰岩的观测点C1~C5,体积含水量如图9所示,几乎无变化,由此可见,从坡面入渗的水集中在土层交界面处,导致交界处的抗剪强度降低,因此交界面处是一条可能的滑动带。该条滑动带发生滑坡的时间大致在降雨20 d,这与实际情况的边坡滑动带位置和发生滑坡的时间相符。

图8 测点B1~B5体积含水量变化趋势

图9 测点C1~C5体积含水量变化趋势
4 结论
(1) 根据降雨入渗与土体渗透系数的关系,模拟了连续强降雨入渗的全过程,从理论上解释了渗流过程中暂饱和态形成的过程和状态,主要是由于非饱和土的渗透系数会随体积含水率的改变而改变,导致坡面和顶层形成了暂饱和态,随时间推移,暂饱和态向下发展速度越来越缓。
(2) 边坡安全系数随着降雨入渗深度的增加而不断降低,这是由于降雨过程中,体积含水量增大,使得基质吸力降低,最终坡体抗剪强度降低,安全系数减小。
(3) 依托衡桂高速公路某路堑边坡工程实例,从理论上提出连续强降雨工况下的渗流原理,并以此为依据进行数值模拟,根据模拟结果推测了边坡失稳的时间以及滑动面的位置,从结果上来看,与实际情况相符,为该边坡的防护工程设计提供了依据。

