带落角约束的非奇异快速终端二阶滑模制导律*
尤 浩,赵久奋,李 朋,宋林浩
(1 火箭军工程大学, 西安 710025;2 中电科仪器仪表有限公司技术支持部, 山东青岛 266000)
0 引言
随着现代战争的快速发展,导弹攻击地面机动目标时,需要导弹以较小脱靶量击中目标同时导弹以指定角度攻击目标[1-2],以提高毁伤效能。
滑模变结构控制理论具有对参数选取的不敏感性和对外部扰动的强鲁棒性[3],因此广泛应用在制导律设计中。文献[4]针对线性滑模面收敛速度较慢的问题,在滑模面中引入线性函数以提高收敛速度,但造成了收敛过程中的奇异问题。文献[5]基于非奇异终端滑模设计制导律的过程中避免了奇异问题的出现,但制导律只适用于攻击静止或弱机动目标。文献[6]提出了一种适用于攻击机动目标的滑模制导律,并设计了非线性观测器对目标机动信息进行估计,但需要目标机动上界,而目标机动上界一般很难获得。文献[7]提出了一种有限时间收敛的积分滑模面,结合快速幂次趋近律,设计了适用于攻击机动目标制导律,并对未知机动目标干扰上界进行自适应估计。但上述文献研究的都是一阶滑模制导律,而二阶滑模制导律具有抑制抖振能力强、鲁棒性强的优点[8],因此基于二阶滑模控制理论设计带落角约束的有限时间收敛制导律具有很强的工程应用价值。
为提高滑模面的收敛速度,并抑制抖振现象,文中基于非奇异快速终端滑模和二阶滑模控制理论设计了带落角约束的有限时间滑模制导律,设计制导律的过程中避免了奇异问题的出现。并设计了非齐次干扰观测器对系统中未知目标机动信息带来的扰动进行估计,无需目标先验信息,有利于工程应用。
1 系统模型建立
1.1 弹目相对运动模型
考虑导弹在二维平面中攻击地面机动目标问题,导弹和目标的相对运动关系如图1所示。
图1中,Oxy是地面惯性坐标系,M和T分别表示导弹和目标。q为弹目视线角,规定由弹目视线r顺时针旋转到水平基准线时为正,反之为负;θm表示导弹M的弹道倾角,θt表示目标T在俯仰方向上的航向角,规定速度位于水平基准线上方时为正,反之为负;vm、am、vt和at分别表示导弹和目标的速度和法向过载。根据图1中弹目相对运动关系,得到导弹末制导数学模型为:
(1)
(2)
(3)
(4)
将导弹速度vm在地面惯性坐标系Oxy两个坐标轴上分解,得到导弹的运动方程为:
(5)
分别对式(1)和式(2)求导,并将式(3)和式(4)代入,得到
(6)
(7)
式中:ur、uq表示导弹M在视线方向上和视线法向上的加速度分量;wr、wq表示目标T在视线方向上和视线法向上的加速度分量。在末制导段,弹目相对速度在视线方向上的分量远小于0,并且弹目相对加速度在视线方向上的分量很小,在只考虑脱靶量和落角约束的情况下,导弹和目标加速度在视线方向上的分量ur和wr造成的影响可以忽略不计,因此将ur和wr设定为0,仅利用式(7)设计视线法向上的制导律uq。uq和wq对应的表达式为
uq=amcos(q-θm)
(8)
wq=atcos(q-θt)
(9)
1.2 带落角约束问题和设计目标
假设导弹击中目标时刻,导弹攻角可以近似为0,则导弹攻击落角可以近似为导弹和目标的弹道倾角之差。设期望落角为σd,则
σd=θmf-θtf
(10)
式中:θmf和θtf为导弹击中目标时刻导弹弹道倾角和目标航向角。根据零化视线角速率思想,导弹击中目标时刻有
-vtsin(qf-θtf)=vmsin(qf-θmf)
(11)
式中:qf为导弹击中目标时刻的视线角。设
(12)
求解式(11)并将式(10)和式(12)代入,得到
(13)
若导弹攻击固定目标,θtf=0,导弹期望落角为攻击时间导弹弹道倾角;若导弹攻击非机动目标,θtf可通过θt的初值得到;若导弹攻击机动目标,θtf可通过弹上跟踪滤波器得到,因此可以假设θtf为已知。由式(13)可知,对于每一个指定的期望攻击角度σd,存在一个与之一一对应的终端视线角qf,因此导弹攻击落角约束问题可以转化为视线角的跟踪问题。

(14)

2 制导律设计
针对系统状态方程式(14),选取非奇异快速终端滑模面如下:
s=x1+k1sig(x1)a1+k2sig(x2)a2
(15)

对滑模面式(15)求导,并将式(14)代入,得
(16)
为使系统状态有限时间内收敛到滑模面,并沿着滑模面运动,在有限时间内收敛到系统期望状态,针对式(16),设计二阶滑模制导律如下:
式中:α和β均为大于0的常数,y>2,z1为下文将要设计的非齐次干扰观测器对系统式(16)中扰动dq的估计值。
对于式(16)中由目标机动信息带来的扰动dq,设计如下非齐次干扰观测器对dq进行估计。
(18)
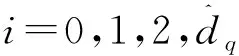
证明: 假设非齐次干扰观测器式(18)在时间tr收敛到系统干扰的真实值dq,则当t≥tr时,将制导律式(17)代入到式(16),化简后得
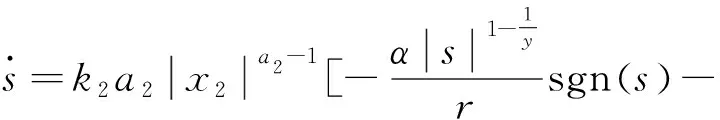
(19)
为方便分析,引入以下状态变量:
(20)
(21)
对式(21)求导可得
(22)
容易发现,矩阵A为Hurwitz矩阵,因此对任意矩阵Q=QT,存在对应矩阵P=PT>0,满足如下代数黎卡提方程:
ATP+PA=-Q
(23)
对系统式(22)选取如下Lyapunov函数:
V1=ρTPρ
(24)
对式(24)求导后将式(22)代入,得到
(25)
(26)
式中:
(27)
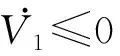
(28)
当|x2|=0,且tr (29) 当t≥ts,即系统状态收敛到滑模面s=0时,则式(15)变为: x1+k1sig(x1)a1+k2sig(x2)a2=0 (30) 对系统式(30),选取Lyapunov函数如下: (31) 对式(31)求导,并将式(30)代入,得到 (32) 将式(31)代入到式(32),化简后得到 (33) 式(33)具有同式(26)结构,由文献[10]中引理1可得,x1在有限时间内收敛到0,并且由式(30)可得,当x1=0时,x2也在有限时间内收敛到0。证毕。 为验证文中提出的制导律式(17)的有效性,设置导弹在不同落角约束下攻击机动目标。仿真参数设置为:导弹和目标的初始位置分别为(5 000 m,5 000 m),(10 000 m,0 m);导弹的速度vm=300 m/s,初始弹道倾角为θm0=-20°;设置目标做常值机动,目标初始速度vt=30 m/s,加速度at=0.4gm/s2,初始俯仰方向航向角为θt0=30°。制导律式(17)中的仿真参数选取如下:a1=3,a2=1.1,k1=k2=1,α=500,β=600,γ=2.1。非奇异干扰观测器中的仿真参数设置为λo=1.1,λ1=1.5,λ2=2,μo=3,μ1=6,μ2=8,L=0.1。 导弹的期望落角分别为σd=-30°,-60°,-90°,制导盲区设置为20 m,即导弹进入制导盲区后按进入制导盲区瞬时的加速度飞行。导弹法向过载限制为30g,g=9.81 m/s2,仿真步长设置为1 ms,得到仿真结果如图2所示。 从图2可以看出,在确定目标的机动方式下,文中提出的制导律式(17)能够击中目标且满足落角约束。法向加速度在制导末期,收敛到0附近的小邻域内,并且收敛过程中光滑无抖振现象出现,有利于导弹自动驾驶仪的控制。视线角速率在制导末期均收敛至0,保证了导弹能够击中目标。滑模面在有限时间内收敛到0,收敛过程中光滑无抖振现象出现。验证了提出的制导律对抖振现象良好的抑制作用。上述的仿真和分析表明,文中提出的制导律针对强机动目标能够满足落角约束的同时以较小脱靶量击中目标,加速度保持在合理的范围内并且无抖振现象出现,验证了制导律的强鲁棒性和工程适用性。 为验证提出制导律的优越性,将非奇异快速终端二阶滑模制导律记为SO-NFTSMG,与标准非奇异滑模制导律[11](记为NTSMG)进行仿真对比,NTSMG的表达式为: (34) 式中:K为符号函数增益,根据目标机动上界选取,本文仿真中选取K=100,式中其余参数同制导律式(17)参数选取。得到仿真结果如表1和图3所示。 图2 3枚导弹攻击机动目标仿真结果 从表1可以看出,两种制导律作用下的导弹落角误差差别不大,但SO-NFTSMG作用下的导弹脱靶量较NTSMG作用下的脱靶量减小约0.18 m,说明制导律SO-NFTSMG有效提高了制导精度。从图3(c)、 图3(d)和图3(f)中看出,SO-NFTSMG作用下的视线角、视线角速率和滑模面在较短的时间内收敛到期望值,验证了制导律SO-NFTSMG快速收敛的优点。从表1中看出,NTSMG作用下的导弹飞行时间较SO-NFTSMG减少约0.6 s,这对于飞行时间较短的导弹末制导段而言,在一定程度上增大了突防概率。但从图3(d)、图3(e)中看出,NTSMG作用下的视线角速率和法向加速度在收敛过程中出现了不期望的高频抖振,不利于导弹自动驾驶仪的控制。而SO-NFTSMG作用下的视线角速率和法向加速度在收敛过程中没有出现高频抖振,验证了SO-NFTSMG抑制抖振能力强的优点。综合而言,文中提出制导律制导精度高,收敛速度快,对抖振现象的抑制能力强,验证了文中提出制导律的优越性能。 基于非奇异快速终端滑模和二阶滑模控制理论设计了带落角约束有限时间滑模制导律。证明了制导律的稳定性和有限时间收敛特性,设计非齐次干扰观测器对目标机动信息进行估计,无需目标先验信息。通过与不同制导律的仿真对比,结果表明:设计的制导律对脱靶量和落角的控制能力强,能控制导弹以较小的脱靶量和落角误差击中机动目标,并且具有制导精度高,收敛速度快,对抖振现象的抑制能力强的优点,具有一定的实际应用价值。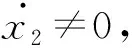
3 仿真分析

4 结论

