风载荷对飞行器尾罩分离影响的数值模拟分析*
孙 伟,陈泽栋
(1 91550部队, 辽宁大连 116000;2 大连理工大学工程力学系, 辽宁大连 116024)
0 引言
采用弹射方式发射的飞行器,一般用尾罩保护一级助推器尾段内的设备及发动机免受高温高压燃气损坏,同时起到承力作用[1]。弹射到一定高度后,采用弹簧或推冲器使尾罩与弹体分离,尾罩上的侧推发动机点火,完成分离动作[2]。尾罩下落时,地面设备和人员为避免被误伤,应当处于落地范围之外。但尾罩的分离过程、飞行轨迹及落地距离在重力、燃气后效、风载荷等因素影响下具有不确定性,应当考虑以上干扰因素,对尾罩分离运动进行全面准确的分析。
贾如岩等[3]、李慧通等[4]分别采用刚体动力学方程结合蒙特卡罗法,模拟尾罩分离运动,虽然得到尾罩落点,但没有考虑分离物与燃气、风载荷的耦合作用,也不是非定常计算。田书玲等采用CFD(computational fluid dynamics)重叠网格技术,对机翼下外挂物投放过程非定常绕流进行了模拟[5],刘君等采用非结构动网格技术,在保证计算精度的基础上,极大提高了具有复杂外形、大幅相对运动问题的计算效率[6]。与单独的刚体动力学仿真相比,采用流体力学与刚体动力学耦合分析,能实现非定常计算,计算结果更精确,方便对分离过程进行研究。
文中建立了发射筒、弹体和尾罩模型,利用非结构动网格技术耦合求解ALE(arbitrary lagrange-euler)描述下的Euler方程和六自由度弹道方程,对飞行器出筒、尾罩分离及下落过程进行数值模拟。主要分析风载荷对尾罩分离、下落过程的影响,最后得到了尾罩的落地范围。
1 计算方法
1.1 控制方程
控制方程采用ALE描述下的三维可压缩Euler方程,其积分形式为:
(1)

(2)
式中:V(i)是与控制体相邻的所有网格单元;∂Ωij为单元i与j的交界面。将对流通量在面元上的积分用数值通量函数近似(如(近似)Riemann求解器),即:
(3)
(4)
对流通量的计算采用AUSM+-up格式[7],时间离散采用二阶时间精度的四步Runge-Kutta格式,边界条件采用固壁边界条件和亚声速远场边界条件[8]。通过求解流体控制方程,获得流场物理量分布,利用获得的流场参数,计算当前时刻尾罩受到的气动力,代入6DOF弹道方程求解下一时刻尾罩的位移、速度、姿态等。
1.2 非结构动网格技术
文中采用非结构动网格技术[9]实现飞行器尾罩分离仿真过程。采用弹簧近似实现网格变形,加入表示扭转弹簧效应的修正因子,提高网格的质量和变形能力,减少标准弹簧近似方法中出现的网格过度扭曲和“折穿”现象,同时还保持较高的计算效率。当网格过度变形导致网格质量变差的区域需进行网格重构,即重新生成计算网格替换原网格,这过程需要在新旧网格之间进行数据传递,不仅影响计算效率,而且会引用插值误差。采用徐春光提出的守恒插值方法提高网格重构时的插值精度[10]。
2 计算模型与结果分析
2.1 计算模型
整个系统如图1(a)所示,包括发射筒、飞行器弹体、尾罩和侧推装置。因为是低速流动问题,为了减小边界误差向内传播对结果产生的影响,将计算外边界取的较远,如图1(b)所示,计算区域取为以原点为球心的半球,半径R=50 m,整个计算模型网格量约为30万,采用四面体单元。坐标系定义如图1(c)所示,原点O位于发射筒轴线延长线与地面的交点,X轴为水平方向,Y轴竖直向上,Z轴构成右手系,风场方向沿X轴正向。定义尾罩质心相对位移为y1,尾罩与弹体底部的纵向距离为y2,尾罩与喷管的纵向距离为y3,尾罩俯仰角为θ(图中为负)。

图1 计算模型与坐标系
弹射飞行器发射时,由发射筒内高压燃气将弹体弹射至一定高度,分离装置解锁,尾罩受分离弹簧作用开始分离。尾罩与弹体达到一定距离后,侧推装置工作,尾罩在推力作用下横向运动。最后侧推装置停止工作,尾罩沿抛物线落到地面。为详细分析风载荷对尾罩分离和下落过程的影响,将整个过程分为两步进行模拟:第一步计算飞行器出筒至横喷发动机启动前的尾罩分离过程,第二步计算侧推装置启动后的尾罩下落过程。风的速度分别为0 m/s和15 m/s,沿X轴正向,其中15 m/s的风速是允许飞行器发射的极限情况。
2.2 尾罩分离过程模拟
第一个计算过程各动作时刻设置如下:t=0 s时,飞行器弹射出筒,来流密度1.23 kg/m3,发射筒出口压力0.65 MPa,飞行器出筒速度10 m/s。t=0.3 s时,飞行器尾罩开始分离,分离弹簧的作用简化为作用于尾罩两端的恒定力,大小4 000 N,作用时间0.1 s,作用方向竖直向下。
t=0~1.1 s尾罩姿态角变化如图2所示。偏航角ψ、滚转角φ受不同风速影响变化不大,俯仰角θ变化大。t=1.1 s,风速0 m/s,尾罩俯仰角θ=1.7°,风速15 m/s,尾罩俯仰角θ=-17.8°,风速15 m/s与无风状态相比,尾罩俯仰角变化增大10倍。
风速0 m/s时,如图3所示,飞行器弹射过程中尾罩底部受燃气后效作用,压力随时间逐渐减小,压力分布沿Y轴对称,压力大小沿尾罩径向逐渐降低。由图2、图3可知,尾罩姿态角变化不大,最大的俯仰角只有1.7°,尾罩装有侧推装置,外形不对称,风速0 m/s状态下姿态角发生微小变化。
风速15 m/s时,气动力对尾罩分离过程的影响分为3个阶段:
1)出筒未分离阶段:如图4(a)所示,尾罩所受气动力主要是发射筒内燃气的后效作用,气动力大,方向沿y轴正向。
2)分离初始阶段:如4(b)所示,尾罩即将分离,此时受到风载荷影响,燃气分布改变,导致尾罩底部沿径向压力分布不均匀,右侧压力高于左侧。
3)分离后期阶段:如4(c)所示,尾罩分离装置解锁,由于分离弹簧的作用,尾罩具有向下运动速度。此阶段尾罩在非对称压力分布的影响下产生绕其质心转动的气动力矩,导致其姿态角发生改变。随着分离时间的增加,尾罩开始进行近似于自由落体的运动。
两种不同风速下尾罩姿态角变化说明:尾罩分离过程中,风载荷会改变燃气分布,影响燃气后效作用,进而改变气动力的大小和分布。由于横向风载荷的影响,气动力使绕Z轴的气动力矩Mz发生较大变化,导致尾罩俯仰角θ产生显著变化。
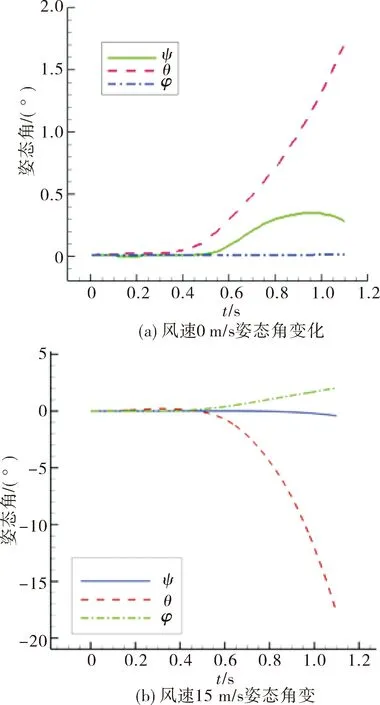
图2 不同风速尾罩姿态角变化对比
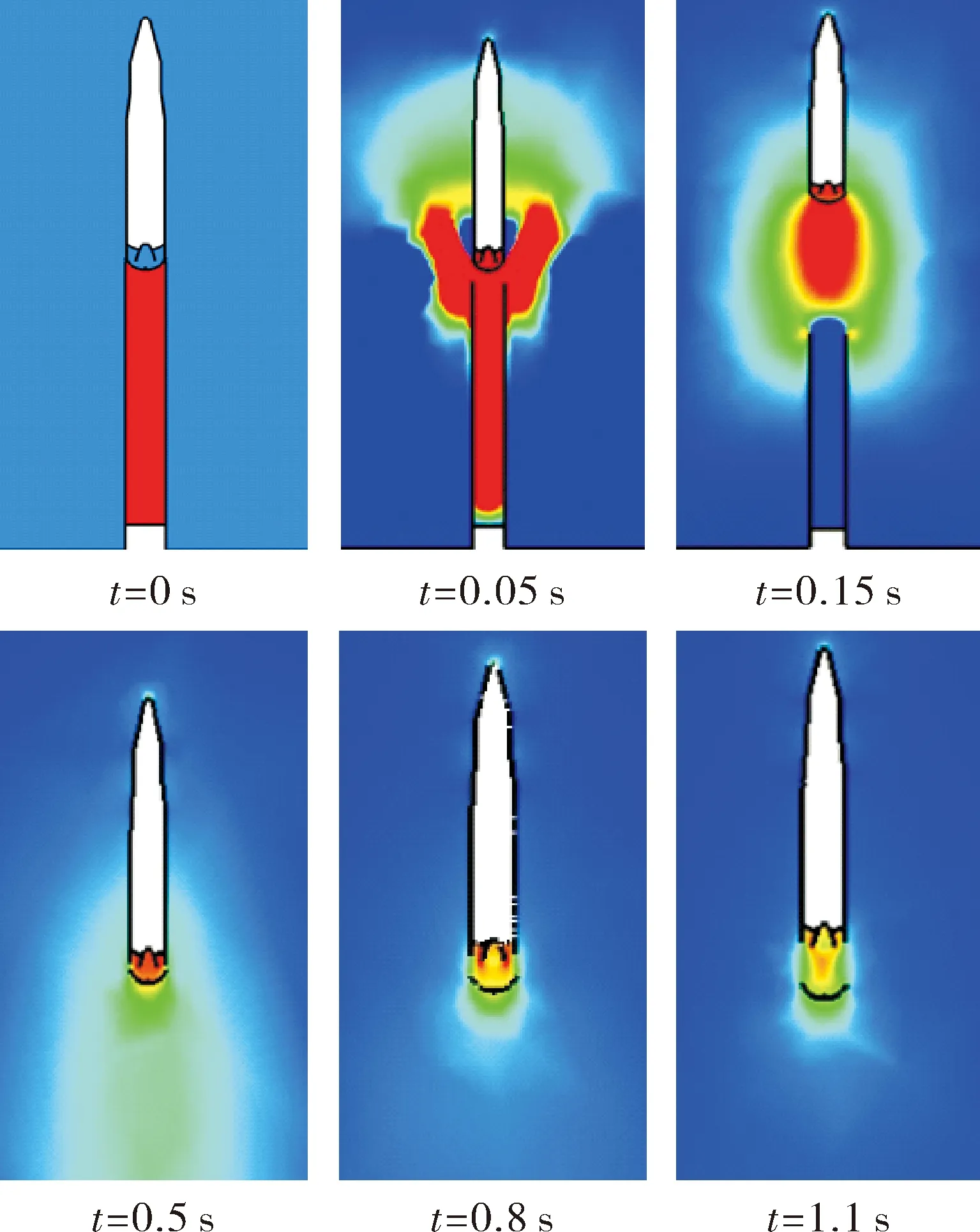
图3 风速0 m/s尾罩分离过程压力云图
2.3 尾罩下落过程模拟
第二个计算过程的初始时刻为t=1.1 s,即侧推装置启动时,到尾罩落地时止。为简化工作,侧推装置产生的推力由加载在尾罩上的初速度代替,该初速度的大小为u=8 m/s,方向与侧推装置产生的推力方向一致。初始时刻尾罩的运动参数是第一个计算过程中t=1.1 s时尾罩的运动状态,风速、来流密度等保持不变。
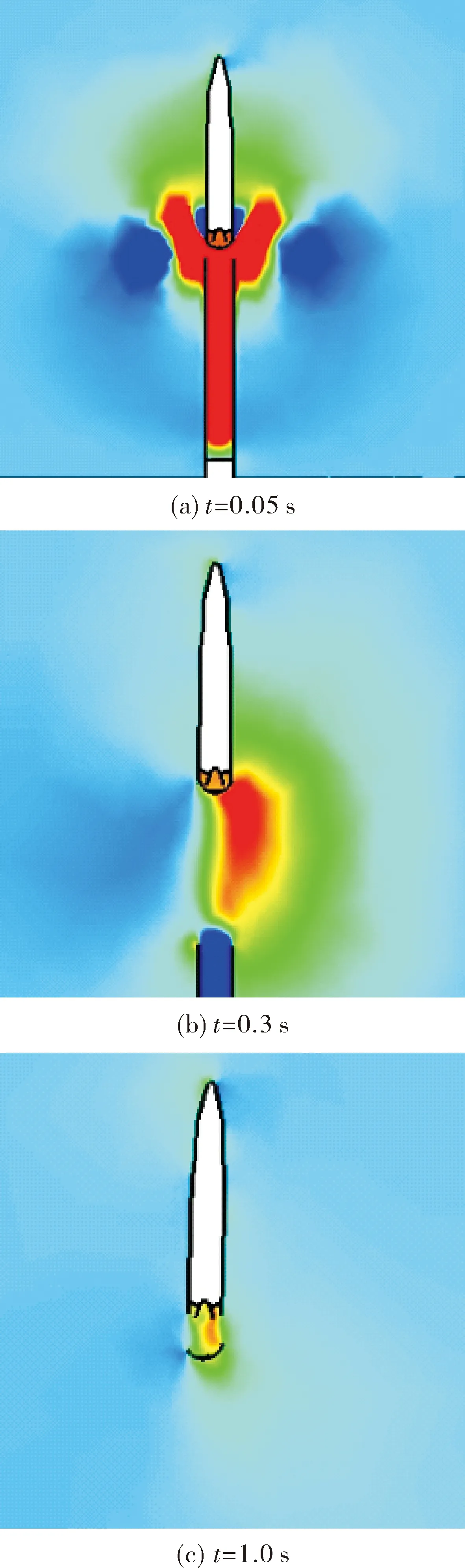
图4 风速15 m/s尾罩分离过程压力云图
尾罩下落过程中,受风载荷影响,姿态角发生明显变化。如图5所示,对比不同风速0 m/s和15 m/s时的姿态角变化,可以看到:风速0 m/s时,尾罩偏航角和滚转角变化不大,俯仰角沿负方向逐渐增大,达到-45°时又逐渐减小;风速15 m/s时,尾罩俯仰角的变化趋势与0 m/s时相似,最大值为±50°,变化幅值大于90°。

图5 不同风速尾罩姿态角变化
图6(a)、图6(b)是风速0 m/s时,尾罩下落过程中不同时刻的压力云图。尾罩周围压力梯度较小,尾罩附近的流体速度变化不大,方向沿Y轴向上。t=0.5 s时,尾罩凹腔内压力小于背部压力,且背部偏上位置的压力更大,因此尾罩俯仰角继续增大。t=2.0 s时,尾罩即将落地,此时俯仰角几乎为0°,尾罩底部压力进一步增大。
图7(a)、图7(b)是风速15 m/s时,尾罩下落过程中的压力云图。与风速0 m/s时相比,尾罩周围部分区域的压力梯度较大。t=0.5 s时,尾罩左右两端压力较大,底部压力较小;t=2.0 s时,尾罩即将落地,此时前端压力特别大,凹腔内压力较小。
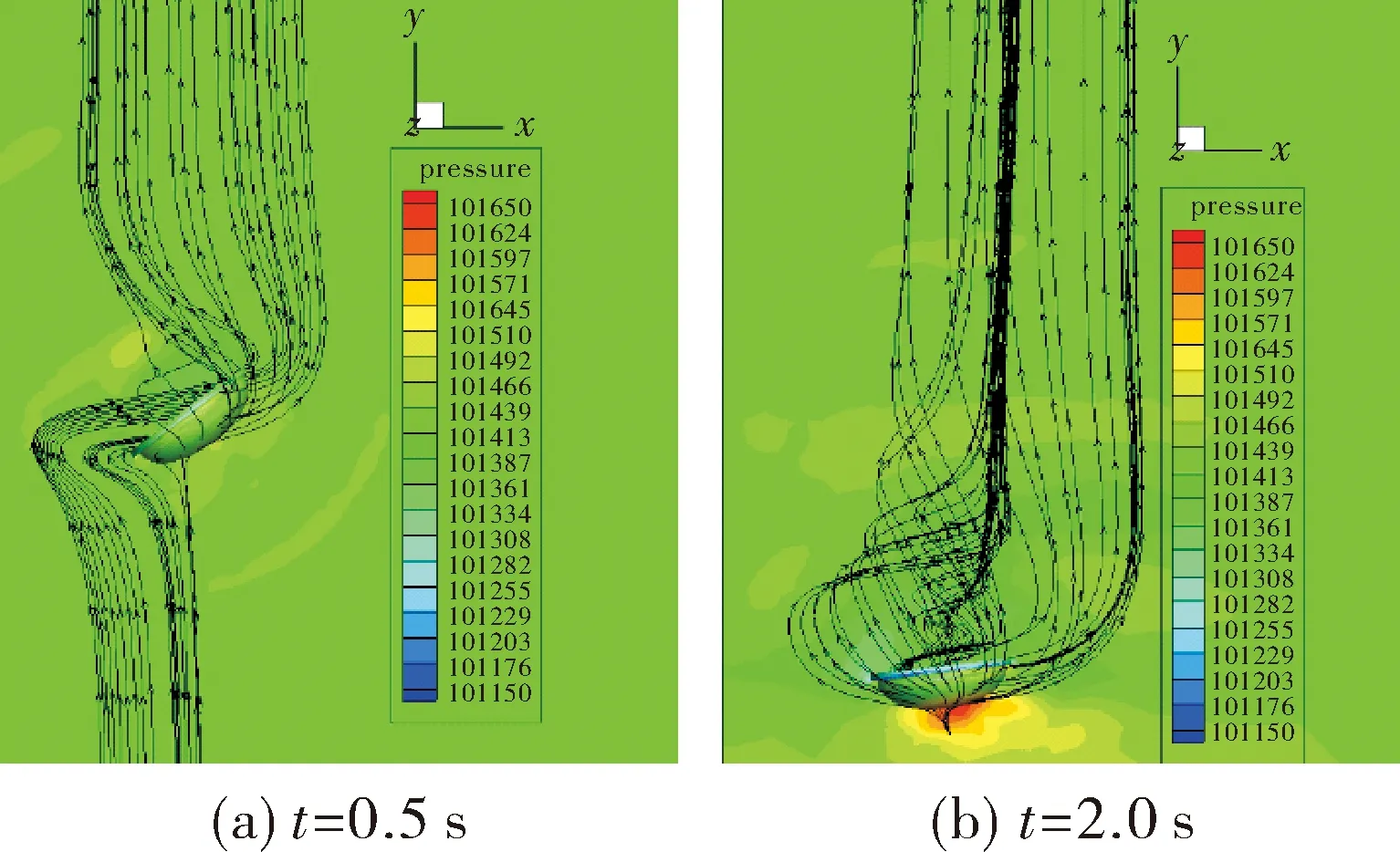
图6 风速0 m/s尾罩周围压力云图
图8是不同风速下尾罩质心的位移对比曲线,风速0 m/s时,尾罩落点的X方向位移为12.37 m;风速15 m/s时,尾罩落点的X方向位移为19.22 m。风速越高,位移越大,位移值均大于10 m。两种风速状态下,尾罩落地距离均小于20 m,所以观测人员在此距离外是安全的。风速 15m/s是发射的极限工况,以此工况为参考设置的安全距离科学可靠。
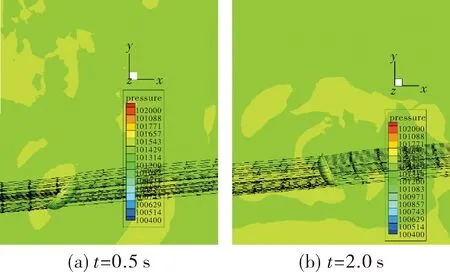
图7 风速15 m/s尾罩周围压力云图
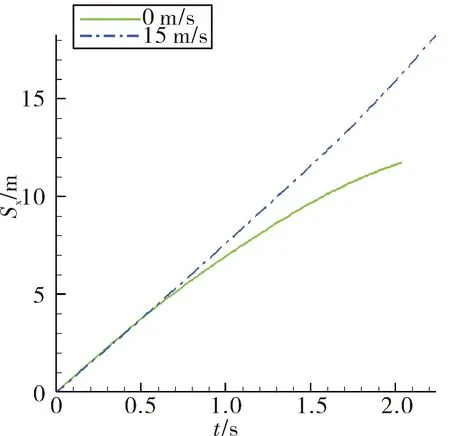
图8 不同风速尾罩位移对比
3 结论
采用非结构动网格技术,对基于ALE描述的欧拉方程和六自由度弹道方程进行耦合求解,对横向风载荷影响下的飞行器尾罩分离过程进行了数值模拟,研究结果表明:
1)横向风载荷会改变燃气分布,进而改变气动力的大小和分布,造成尾罩俯仰角显著变化。
2)横向风载荷使尾罩的落地距离更远。0 m/s、15 m/s两种风速状态下,尾罩落地距离均小于20 m,安全距离设置为20 m以外是可靠的。

