基于跳跃机动的高超声速飞行器速度控制方法*

蔡艳芳,李晓松,陈 韵,张文渊

(1 西安现代控制技术研究所, 西安 710065;2 西安电子工程研究所, 西安 710100)

0 引言

高超声速飞行器联合作战是提高飞行器作战效能的有效途径,但高超声速飞行器再入后滑翔速度快、轨迹包络大、姿态变化快,任务空间维度跨越范围广,飞行器需要在指定的时间段完成飞行任务,因此高超声速飞行器再入后的速度控制成为任务成败的关键[1-3]。

自20世纪60年代阿波罗飞船采用跳跃式轨道返回地球以来,跳跃机动技术由于较强的减速和轨迹控制能力得到了快速发展和广泛应用。赵钧[4]以高超声速临近空间飞行器连续跳跃飞行为研究对象,利用遗传算法对一个飞行周期的跳跃飞行轨迹进行了优化,该方法适合于离线的高速飞行器弹道优化,但计算量巨大不适合工程应用。陈海兵[5]分析了跳跃段后期末端下滑段导引系统的特点,给出了限定落角落速的伪最优导引律计算方法,但将速度大小和方向控制分开设计的最优导引律难以同时达到二者最优;王银、杜昕[6-8]等针对月球返回舱跳跃再入大气层问题,采用庞特里亚金极大值原理对过载约束下再入轨道的初始再入段进行了优化设计,由于模型简单,仅适用于载人月球返回舱的初步设计。

文中从高超声速飞行器跳跃机动轨迹的物理机理出发,提出了一种通过跳跃轨迹实现飞行器速度控制的制导方法,设计了基于跳跃机动的速度控制策略,并通过仿真计算验证了该方法的正确性与有效性,对实现飞行器联合作战具有一定的工程实用价值。

1 飞行器跳跃机动的物理机理分析

高超声速飞行器滑翔过程中主要受到气动参数摄动、外界干扰以及发动机参数等各种不确定和时变因素的影响[9],导致飞行器再入后的速度散布很大。为满足飞行速度的指标要求,导引过程中必须对飞行器速度变化规律进行控制,使飞行器沿着满足速度约束条件的理想运动轨迹飞行。

地球大气层垂直方向上的大气密度差异明显,在距地球表面15 km和30 km高度处,大气密度分别约为地面的16.179%和1.602%[10]。通过制导控制下跃和拉起轨迹,增大飞行过程中受到的平均阻力,实现纵向平面内一定跨度的跳跃前进,能够快速降低能量过剩飞行器的飞行速度。通过解析方法分析跳跃机动对飞行器气动力影响的物理机理。

(1)

2 跳跃机动的高度边界

2.1 约束指标对跳跃机动的影响

跳跃机动制导过程应充分考虑以下因素:

1)高超声速气动加热对热防护的影响;

2)过载对飞行器结构、执行机构的影响;

3)动压对飞行器控制系统和稳定性影响。

在一定简化的条件下,将各约束条件表述为高度与速度的函数关系式:

1)热流密度约束

(2)

2)动压约束

(3)

3)法向过载约束

(4)

在典型轨迹条件下,跳跃机动在多指标约束条件下的高度边界如图1所示。

2.2 高度跳跃的下边界

高度跳跃的下边界是描述飞行器跳跃制导的允许最低轨迹高度。在向下跳跃制导过程中,飞行器一旦低于一定高度,不仅可用攻角、过载不能满足约束要求,而且可能导致速度损失过大,出现能量不足的情况。高度跳跃的下边界是由飞行器与虚拟目标的飞行速度之差决定的,随飞行马赫数的变化而变化。

图1 跳跃机动的高度边界

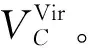
由以上分析可知,若飞行器攻角先减小后增大,沿ABD轨迹飞行的速度损耗低于攻角持续为负的ABC轨迹的速度损耗。由于导弹再入后保持无动力飞行,为了保证跳跃机动后飞行器的速度VD(t)依然略大于虚拟目标飞行速度VVir(t),通过制导控制使飞行器沿ABD所示规律的轨迹飞行是一种可行的速度控制策略。因此B点对应的高度即为飞行器跳跃机动的下边界。

图2 向下跳跃机动的飞行轨迹

3 跳跃机动的制导策略与方法

3.1 跳跃机动的飞行轨迹预测

跳跃制导的目的是在各种偏差和不确定因素影响条件下,飞行器跳跃机动后保持平衡滑翔高度飞行时的速度V(i)(t)等于或接近VVir(t)。飞行器跳跃下降过程中需实时根据当前飞行状态预测返回滑翔高度时的速度Vpre(t),当实时预测的D点速度Vpre(t)大于虚拟目标速度VVir(t)时,停止跳跃机动,提前转入跳跃上升段。

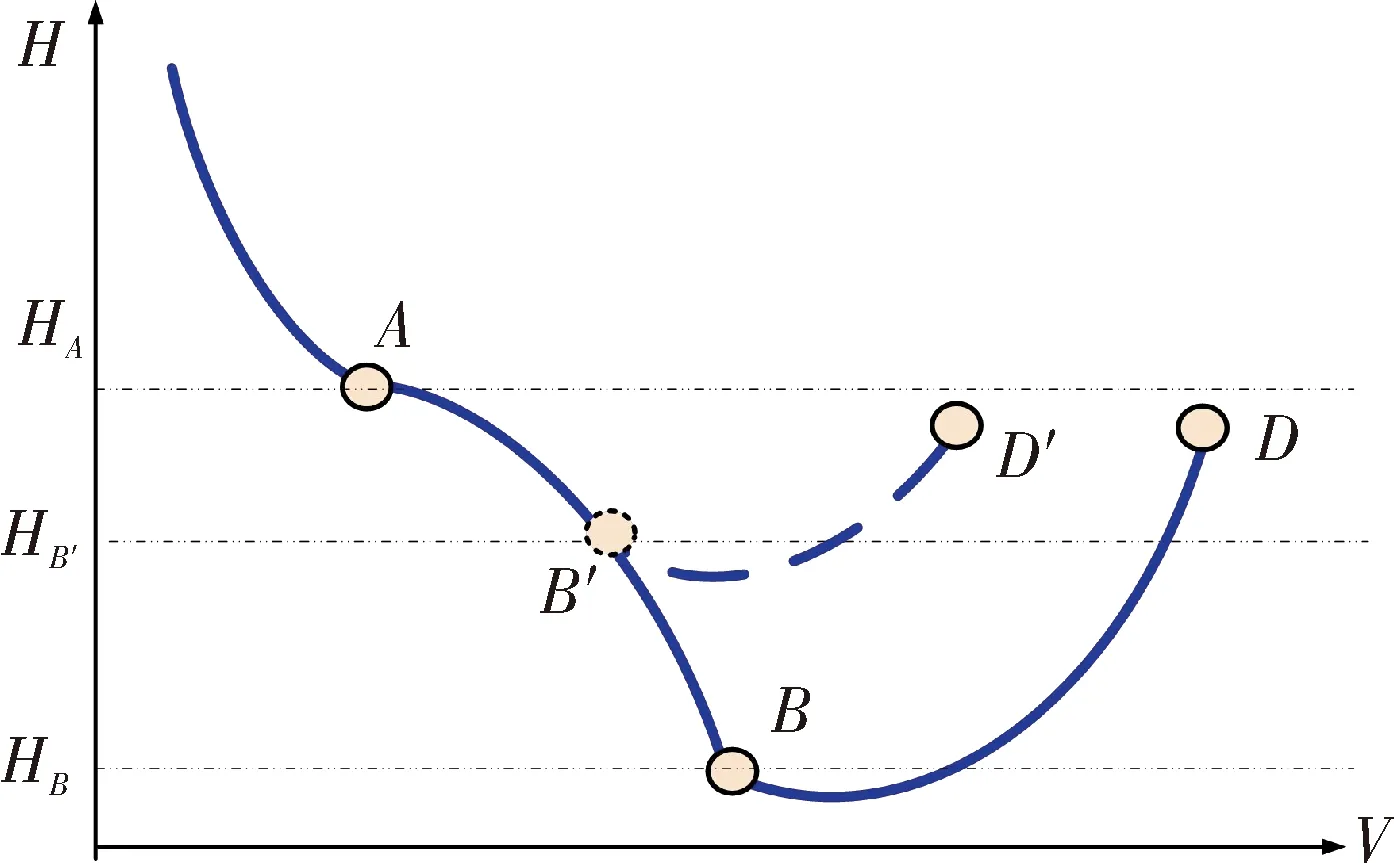
图3 跳跃机动飞行轨迹

为了实时计算跳跃机动的下边界、跳跃拉起点以及拉起后保持滑翔高度飞行时的速度,基于飞行器简化运动模型整理得到的基于高度和速度的质点动力学方程如下:

(5)

若已知飞行器再入下降某点的飞行轨迹参数,根据式(5)按高度步长积分可以得到从初始点之后跳跃过程中的速度、速度倾角。

3.2 跳跃机动制导方法

飞行轨迹跳跃制导分为跳跃上升段和跳跃下降段。在跳跃下降段中,一方面为使飞行轨迹更为陡峭,另一方面考虑到射程要求,需要飞行轨迹迅速下降至预测跳跃高度附近后迅速拉起。该段对速度倾角变化率的要求是迅速下降,当速度损耗达到一定程度后,再在波谷附近迅速提高至零值,从而速度倾角要求先取负的最小值,使飞行轨迹尽量下压,再转为取正最大值,尽快增加速度倾角。具体体现在攻角控制量α为先取负最小值,再转为正最大值。按照一般经验公式,α由再入下降攻角指令变化到最小值的规律采取斜坡下降方式:

α(t)=max(αcmd-kαt,αmin)

(6)

α(t)=min(αmin-kαt,αmax)

(7)

跳跃下降段与跳跃上升段、跳跃上升段与滑翔机动段之间的攻角指令需要采取指令平滑过渡措施。若令加速度矢量为连续函数,交班完成时的加速度等于后段制导律所需的加速度指令,可转化为以两个常值矢量为始末点的两点边值问题,攻角指令平滑过渡的一般形式为:

可以以交接时间t为变量,交接段时间不宜过长,否则飞行器姿态、位置可能会发生较大变化,给跳跃机动速度控制精度造成较大误差。

当飞行器高度逐渐接近滑翔高度时,通过指令平滑逐渐过渡到具有高度约束的滑翔制导控制,通过高度反馈使飞行器沿滑翔高度H*保持平飞,具有高度约束的滑翔制导律为：

(8)

式中：αcmd为平衡滑翔抵消重力所需的攻角指令;Kd、Kp为增益系数。

3.3 跳跃机动制导策略

3.3.1 虚拟目标的设计方法

为简化设计,在标准状态条件下设计虚拟目标的运动轨迹,并将标准状态的飞行器速度、位置曲线作为装订量装订在飞行控制器中。飞行过程中,以时间作为基准量,计算当前状态的虚拟目标位置、速度等信息。各飞行器根据自身位置与虚拟目标的位置、速度关系,进行在线速度控制。同时,为了简化设计,令虚拟目标再入拉起的起始时刻为t0,虚拟目标的速度曲线可拟合为：

龙庆峡位于北京市延庆区，距北京城区85公里。我们一路来到景区，走上一段山坡，看到一块巨石上写着“龙庆峡”三字，我不禁欢呼了一声：“我们到了龙庆峡啦！”

VVir(t)=VVir(t0)-k(t-t0)

(9)

为了判断再入拉起后飞行器与虚拟目标的位置关系,虚拟目标的射程曲线可拟合为：

XVir(t)=XVir(t0)+VVir(t0)(t-t0)-0.5k(t-t0)2

(10)

3.3.2 跳跃机动的制导策略

跳跃机动的制导策略如下:

步骤1:判断飞行器与虚拟目标在飞行方向上的位置偏差和速度偏差

步骤4:停止飞行轨迹下跳,通过高度控制使飞行器保持滑翔高度H*平飞。

图4 时间-速度曲线

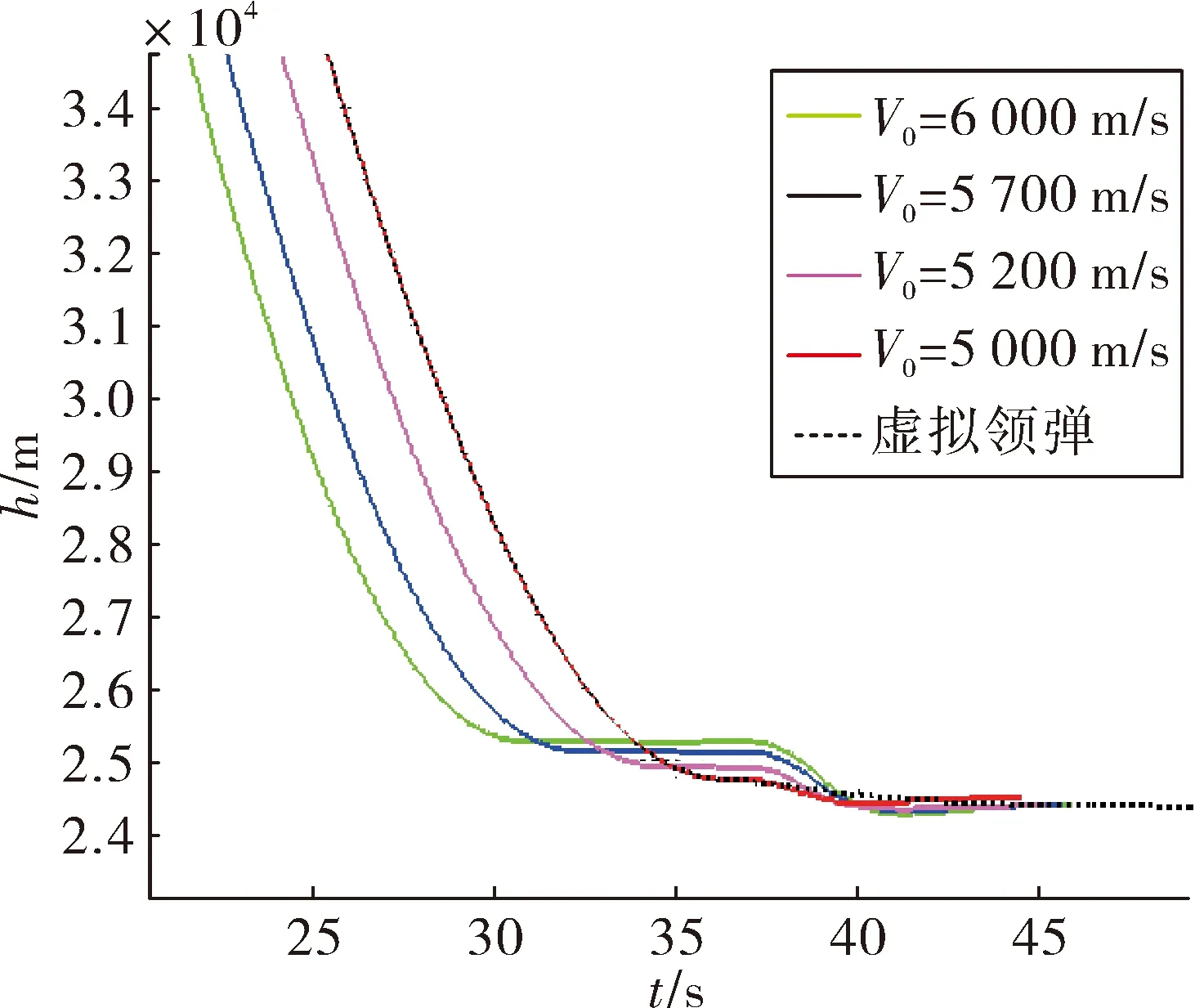
图5 时间-高度曲线(局部放大)

4 跳跃机动的控制性能仿真

以某型高超声速飞行器仿真为例,研究跳跃机动导引策略的性能及速度控制能力。假设飞行器1、2、3、4的初始速度分别为6 000 m/s,5 700 m/s,5 200 m/s和5 000 m/s,速度控制精度要求小于50 m/s。仿真结果如图4～图7所示,轨迹参数如表1所示。

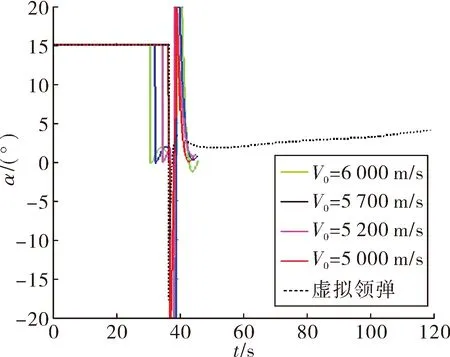
图6 时间-攻角曲线

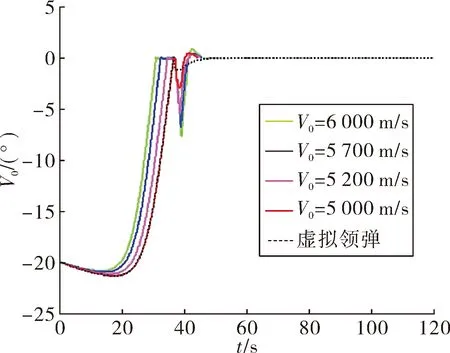
图7 时间-飞行轨迹倾角曲线

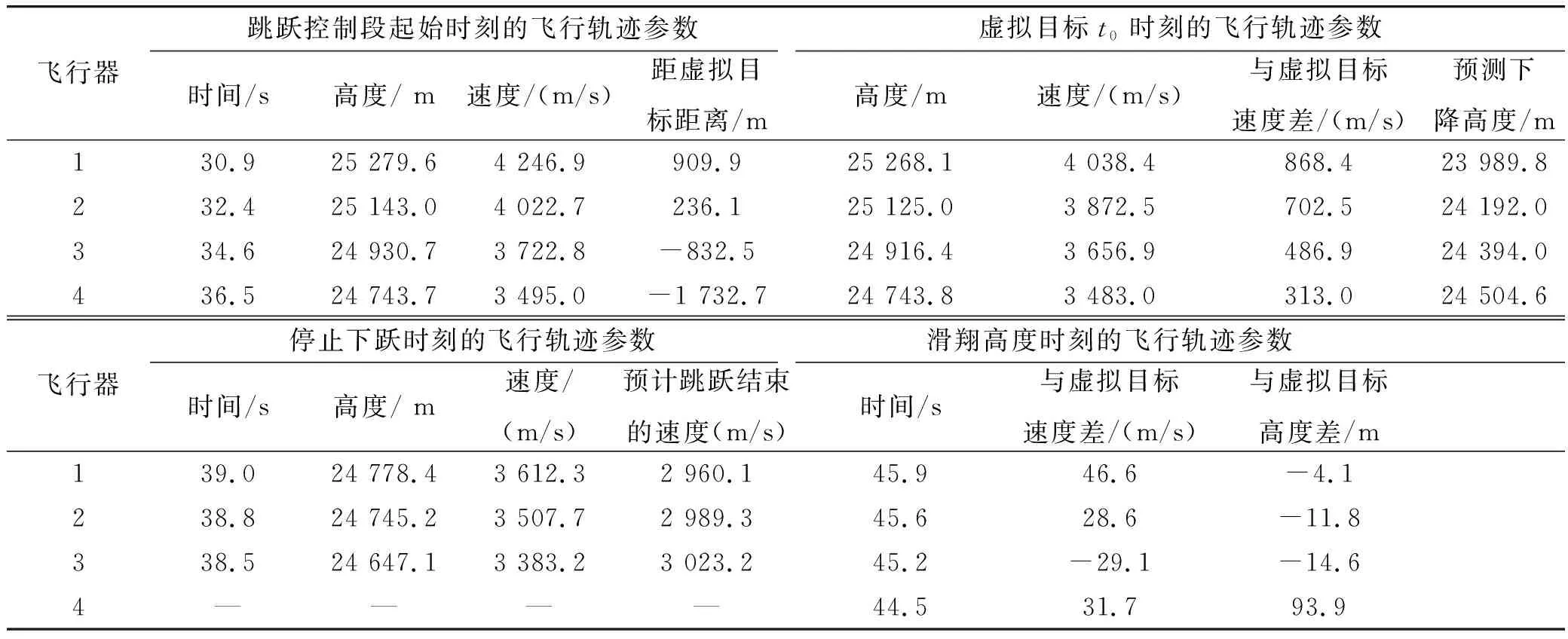
表1 跳跃控制主要飞行轨迹参数

飞行器1在30.9 s时大攻角拉起结束进入跳跃控制段,此时的飞行高度为25 279.6 m,与虚拟目标距离偏差为909.9 m。通过高度控制使导弹沿设计的滑翔高度飞行,并以当前飞行状态为初值,预测跳跃机动的下降高度为23 989.8 m。跳跃机动过程中,在39.0 s时终止跳跃机动,此时飞行器高度为24 778.4 m,速度为3 612.3 m/s,通过高度控制使导弹回到滑翔高度飞行。跳跃机动后,45.9 s时保持平衡滑翔高度飞行,飞行器与虚拟目标的速度差为-4.1 m/s。飞行器2工作状态与飞行器1类似，跳跃机动后，45.65 s时保持平衡滑翔高度飞行。

相比于飞行器1初始飞行速度较大,飞行器3和4的初始速度仅为5 200 m/s和5 000 m/s,飞行能量相对不足,t0时刻与虚拟目标的速度差为486.9 m/s和313.0 m/s。飞行器3在38.5 s时停止机动下跃,保持滑翔飞行时刻的速度差为-29.1 m/s。飞行器4由于能量不足,跳跃机动的预测下降高度高于滑翔高度,故采用具有高度约束的比例导引保持编队滑翔高度平飞,44.5 s时与虚拟目标的速度偏差为31.7 m/s。由典型条件下的仿真结果可以看出,通过基于跳跃机动的速度控制方法能够有效降低飞行器速度,实现了速度控制的要求,且具有较好的速度控制精度。

5 结论

针对高超声速飞行器的速度控制问题,提出了一种基于跳跃机动轨迹的速度控制方法,推导了飞行器在线轨迹预测模型,设计了基于跳跃机动的速度控制策略,实现了不同初始滑翔速度条件下跳跃机动导引的速度控制效果,对解决高超声速飞行器速度控制问题提供了有益的参考。