“四会”:提升数学学习力的关键
张卫星
有价值的数学课堂应该着力提升学生的数学学习力。现在的好多学生最怕自己学不好数学,究其原因是数学学习需要理性思维的参与,需要良好的学习方法。但当下的好多教师更多关注的是学生知识的習得,而忽视了学生学习力的提升。如何提升学生的学习力?关键是要让学生学会“四会”——会动、会想、会问、会理。一旦学生学会了“四会”,数学学习力就将大大提升,数学核心素养的达成也就水到渠成。
一、会动——让抽象的数学更直观
小学数学知识虽然抽象,但有些知识一经动手操作就变得直观而又浅显。因为小学生的思维正由具体形象向抽象过渡,还离不开直观形象的支撑。因此,数学教师要努力将数学知识化静为动,努力为学生创设动手操作的机会,力求让学生在“动”中领悟知识的本质。
例如,在教学人教版数学四年级上册“烙饼问题”时,笔者就刻意为每两个同学准备了3个圆形纸片(代表烧饼),并在每个纸片的正面写上“正”字,反面写上“反”字。在学生动手操作体验烙1张饼和2张饼的时间后,马上动手操作,研究烙3张饼所需要的时间。为此,笔者和学生一起经历了如下教学过程:
师:他们要尽快吃上3张饼,最少需要几分钟?
生:9分钟。
生:我认为是6分钟。
师:咱们先请用时9分钟的同学上来烙一烙,好不好?
生:先把两个饼的正面贴在锅里(黑板预先画了圆,代表锅),一、二、三,熟了。
生(齐):3分钟。
生:把第1张饼翻过来,烙反面;把第2张饼移到锅外等候;把第3张饼移进来,烙正面。一、二、三,熟了。
生(齐):又是3分钟。
生:第1张饼熟了,再烙第2张饼的反面和第3张饼的反面。一、二、三,熟了。
生(齐):又是3分钟。
师:3张饼都烙熟了吗?
生(齐):熟了。
师:一共用了几分钟?
生:9分钟。
师:他们用了9分钟,你们有什么要说的?
生(刚才说6分钟的):我觉得我们烙错了。
师:烙熟3张饼至少需要几分钟?
生:9分钟。
师:让我们来回忆一下,他们是用什么方法把这3张饼烙熟的呀?(生说,师用配套课件演示后在黑板画出和教材一样的示意图)
上述教学,因为学生有了动手操作的体验,所以复杂的烙3张饼的问题就变得有序、清晰、明了。而这种体验即使过了很长时间,学生依然会深深地印在脑海里。可见,让学生学会动手操作既可以让抽象的数学变得直观形象,又可以让学生潜移默化地感受学习数学的方法,不知不觉中提升了他们的学习力。
二、会想——让抽象思维落地生根
数学学习是一个思维加工的过程。只有充分激发学生的思维参与,学生的抽象思维才能早点落地生根。学生的抽象思维需要任务来驱动,“数学学习单”是以学习任务为驱动,激发每一位学生自主学习的活动单。因此,在数学课堂教学中,教师要学会将知识分解成一个个活动或者问题来指导学生的学习活动,促进学生的抽象思维发展。
例如,在教学人教版五年级数学上册《平行四边形的面积》时,笔者设计了如下的学习单:
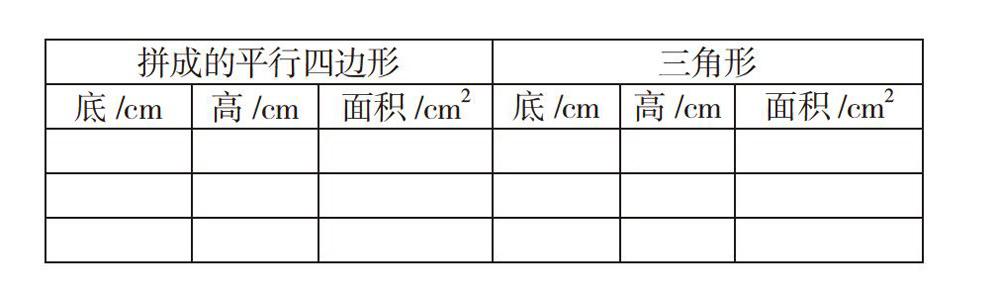
任务1:拿出信封,从中选择两个三角形,先拼一拼,再求出拼成的平行四边形和每个三角形的面积,完成下表。
任务2:观察表格,你有什么发现?小组交流。
在此基础上,教师引导学生着力回答如下3个问题:
(1)拼成的平行四边形和两个三角形有什么关系?
(2)拼成的平行四边形的底和高与三角形的底与高有什么关系?每个三角形的面积与拼成的平行四边形的面积有什么关系?
(3)根据平行四边形的面积计算公式,怎样得出三角形的面积计算公式?
在上述教学片断中,教师以学习单为载体,开展了两次学习活动。第一次活动旨在“有选择地拼”,引导学生在动手操作中初步体会三角形与平行四边形的关系;第二次活动旨在“有问题地思”,引导学生在层层推进的问题中深度思考。问题(1)是在第一次活动基础上的再次感知;问题(2)借助课件“表格中数据”的闪动,用数据说话,加深体验三角形的底、高、面积与平行四边形的底、高、面积的对应关系;问题(3)旨在“有序地推”,引发学生将问题转化成语言的有序表达和思维的有序推理,从而掌握和理解三角形面积计算公式的推导过程。由此可见,引导学生学会思考是提升学生学习力的重中之重。
三、会理——让数学思维更有条理
数学知识逻辑性比较强,要想学好数学,必须具备思维的条理性。但思维的条理性不是天生就有的,需要教师有意识地去培养,让学生在不断的体验中自然而然地形成思维的条理性。因此,教师要根据教学内容适当创设让学生梳理的机会,让学生在思考和梳理中变得更有条理,从而有效提升学习力。
例如,在教学人教版数学六年级下册“立体图形的复习”时,笔者经历了如下的教学过程:
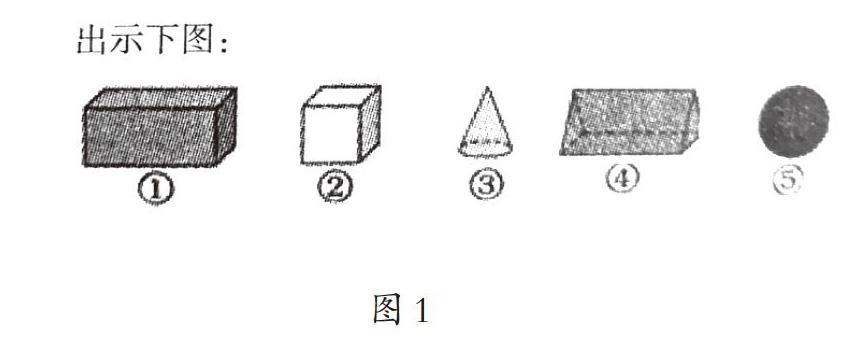
师:下面这些立体图形(如图1),你们认识吗?你们觉得哪几个立体图形可以和圆柱归为一类?
生:我觉得①②④三个图形可以和圆柱归为一类,因为它们都是由一个平面图形平移后得到的。
师:哪些同学和他的归类方法是一样的?(大部分学生举手表示赞同)这几个立体图形还有其他相同的地方吗?
生:它们还有共同的体积计算公式:体积=底面积×高。
生:它们还有共同的表面积计算公式:表面积=侧面积+底面积×2。
师:说得好!它们还有共同的侧面积计算公式:侧面积=底面周长×高。
师:它们的侧面有什么特点?
生:它们的侧面沿高展开都是长方形。长方形的长相当于立体图形的底面周长,长方形的宽相当于立体图形的高。
生:我还知道,这些立体图形都是上下一样粗,数学上叫直柱体。
师:刚才,同学们从整体上对直柱体作了更全面的梳理。我们还可以把哪些圖形归类呢?
生:还可以把③号和⑤号图形和圆柱归为一类,因为它们都有圆形的截面。
师:把③号和⑤号图形和圆柱归为一类,还有不同的理由吗?
生:这几个立体图形都可以由一个平面图形旋转后得到……
师:如果圆柱和圆锥等底等高,老师建议同学们可以把圆柱和圆锥归为一类。
生:我知道了。因为在等底等高的情况下,圆锥体积是圆柱体积的1/3。
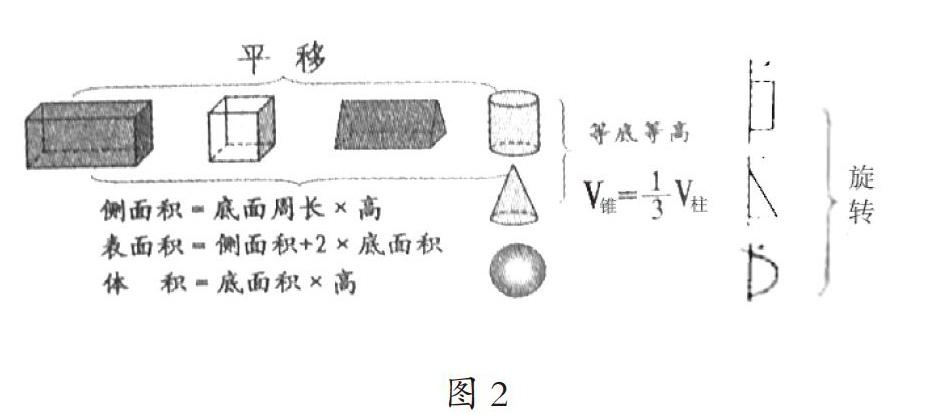
教师根据学生的回答形成如下板书(如图2):
图2
师:同学们,用归类的方法一类类地看图形,可以帮助我们更好地了解图形之间的联系。
教学中以“哪些立体图形可以和圆柱分为一类”作为突破口,通过归类激活,唤醒已有的知识、方法及经验,重建认知结构。学生从不同角度阐述分类理由,进行整体建构,并以“平移”“旋转”等方式再现与强化训练了立体图形的内在联系,很好地完成了对单元知识纵向和横向的结构化整理。在这个整理过程当中,学生的学习力自然而然就增强了。
四、会问——让数学思维更加主动
当下的孩子由于内心惧怕数学,一般不敢主动向教师提问,再加上学生与生俱来的思维惰性,主动提问的可能性就更少。而会问,恰恰能体现出一个学生思维的主动性和灵活性。因此,作为数学教师,要努力创设让学生提问的时间和空间,让学生在提问的过程,感受成功的快乐,从而逐渐抛弃思维的惰性,让主动思维伴随其左右。学生会主动思维了,学习力也就大大提升了。
例如,在教学人教版四年级数学上册《四边形的特性》一课时,笔者经历了如下的教学过程:
师:请拿出事先用学具搭好的长方形模型,捏住上下对角的两个顶点,向两端轻轻一拉,复位,再轻轻一拉。(学生学着做)
师:你们发现了什么?
生:长方形一拉就变成了平行四边形。(板书:长方形→平行四边形)
生:长方形一拉,四边形就变矮了。
生:往回一拉,平行四边形又变成了长方形。
生:往回一拉,四边形又变高了。
师:刚才的回答都正确,长方形一拉、一回,形状就变了,说明平行四边形容易变形。(板书:容易变形)
师:听了刚才的回答,你们有什么要问的吗?
生:为什么长方形一拉就矮了?
师:你的问题很有价值,谁来解答?
生:长方形一拉,高就变短了,所以就矮了。
师:嗯!你的回答很精彩!(板书:高变短)
师:还有什么问题?
生:长方形一拉,高变短了,还有什么变了?
生:拉得厉害一点,就很矮了,说明面积变小了。
师:面积变小了,大家同意吗?大家再拉一下,看看面积是否变小?(学生一拉,纷纷同意,师顺势板书:面积变小)
师:还有什么问题要问?
生:长方形一拉,什么没变?
生:四根小棒没变。
生:四根小棒的长度没变。
生:应该是长方形的周长没变。
师:周长真的没变吗?再观察一遍。(发现真的没变,师顺势板书:周长不变)
师:同学们真厉害!提出了这么多好问题,也发现了这么多新的知识!请大家再仔细看看板书,想想长方形拉成平行四边形蕴含着什么数学知识?
生:长方形拉成平行四边形,高变短,面积变小,周长不变。
上述教学,先通过拉一拉,让学生感受到长方形和平行四边形的互化,从而体会到四边形容易变形的本质。在此基础上,教师提出“你们有什么问题要问的”,迫使学生努力梳理刚才的拉动过程,提出了老师心中最想要的三个问题,从而较为系统地理解了长方形拉成四边形的变化规律。事实上,学生提问的过程就是学生努力思考、主动思考的过程,没有思考就没有问题。试想一下,如果教师经常引导学生提问,学生的主动思维能力能不提升?学习力能不提升?
总之,让学生会动、会想、会理、会问,是提升学生数学学习力的关键。而要达成这种效果,前提是教师要从学生的视角出发设计教学,要充分激发学生主动学习的兴趣,让学生全方位地参与数学学习。俗话说:教是为了不教!只要我们坚持锤炼学生的“四会”能力,学生的数学学习力和数学核心素养一定会得到意想不到的发展。
——《烙饼问题》教学实录与思考

