考虑安装面特性参数的悬臂梁固有频率分析
向民奇,毛汉领,黄悦峰
(广西大学机械工程学院, 广西南宁530004)
0 引言
固有频率是机械结构振动模态的最基本信息,基于固有频率对悬臂梁进行相应研究相关学者已作了很多贡献,张佳文等[1-3]对裂纹位置与裂纹深度与悬臂梁固有频率的关系进行了计算和分析。刘天亮等[4]对悬臂梁建立了基于固有频率的损伤定位理论基础。崔凯等[5]分析了可以简化为旋转悬臂梁模型的风机叶片的叶片长度、旋转速度及叶片截面的弦长与固有频率的关系。
上述研究对悬臂梁的分析都是以振动特性中的固有频率为基础,所以固有频率的精确估算与否对分析结果有着直接影响。而结构的振动特性与其所处的边界约束条件密不可分,尤其对于机械结构而言,各零件间的联接存在多种方式,造成零件间接触面的复杂性和多样性。对于界面间的接触问题,张福星等[6]等利用ANSYS-workbench软件对深沟球轴承建立了三维非线性接触模型,对轴承间的接触应力与变形进行了仿真计算。KUMBHAR等[7-8]利用ANSYS建立了零件装配体的有限元模型,分析接触面间接触刚度、接触变形及接触载荷的关系。艾延廷等[9]基于有限元建模方法分析了装配体接触面法向接触刚度对装配体振动模态的影响。CHEN等[10]采用接触单元分析了热配合转子对空心轴局部刚度的影响。张立军等[11-12]研究发现制动盘的帽部螺栓孔的位侈约束对制动盘整体组合模态的影响很大,施加约束会使模态频率增加,且发现随着制动盘刹车时盘面接触的位置不同将导致不稳定模态计算结果。黄梓嫄等[13]针对磁悬浮电机转子系统模态分析误差较大的问题,提出考虑转子组件间的非线性接触行为,基于罚函数方法通过修正优化接触刚度因子实现对电机柔性转子系统模态的精确分析。杨帅等[14]针对固定端部竖直方向为弹性约束的悬臂梁结构进行了模态分析,并通过固有频率对端部刚度进行识别。李全通等[15]对叶片轮盘典型榫接结构的接触刚度进行了分析,给出了叶轮间接触刚度的计算方法,建立了叶片轮盘榫接耦合计算模型。
悬臂梁是工程应用中常见的一种梁结构,在机械、土木等领域内广泛应用。接触对工程结构的振动特性影响十分复杂,给结构振动分析及实际应用造成很大影响。
本文针对以上提及的问题,首先在ANSYS-workbench软件中对悬臂梁进行模态分析,并同时利用欧拉—伯努利梁理论对悬臂梁固有频率和模态振型进行理论求解,对比有限元分析和理论推导两者的结果具有较好的一致性,说明在ANSYS-workbench软件中对悬臂梁进行模态分析是可行的,并进一步分析悬臂梁安装约束端接触面的接触刚度(本文中均指的是法向接触刚度)和摩擦系数对其固有频率的影响。
1 悬臂梁固有频率及模态振型的理论计算
当梁的长度远大于其截面的高度时,梁的横向弯曲振动频率要远低于它纵向振动和扭转振动的频率,因而梁的横向弯曲共振模态比较容易激发出来。故本文仅考虑弯曲引起的变形,不计剪切引起的变形及其转动惯量的影响,满足欧拉—伯努利梁分析的条件。以悬臂梁的固定端为坐标原点O,梁长的方向为x轴,梁振动方向为y轴,建立等截面悬臂梁的坐标系,如图1所示。

(a) 弯曲时整体分析

(b) 弯曲时微元段分析
图1 悬臂梁的横向振动受力分析
Fig.1 Transverse vibration force analysis of cantilever beams
悬臂梁在y方向的运动方程为:
(1)
式中,ρ为梁的密度(kg/m3);A为梁的横截面面积(m2);L为梁的长度(m);I为梁的截面形心惯性矩(m4),E为梁的弹性模量(GPa);y(x,t)为梁的横向位移(m);f(x,t)为梁所受的横向力(N);Q(x,t)为梁所受的剪切力(N);M(x,t)为梁所受的弯矩(N·m)。
由材料力学中弯矩与挠度及剪切力的关系,等截面匀质直梁的横向弯曲自由振动方程为:
(2)
求解式(2)需两个初始条件和四个边界条件。
初始条件为:

悬臂梁的边界条件为:


求解方程(2)可得
cosλnLcoshλnL=-1(n=1,2,3…),
(3)
用Matlab求解式(3)超越方程得其数值解为:
λ1L≈1.875;λ2L≈4.694;λ3L≈7.855;λ4L≈10.995;λ5L≈14.237;λ6L≈17.278,
则等截面匀质直梁的前6阶固有频率可由(4)式解出
(4)
对应的振型函数为:
(5)
本文所设置的悬臂梁参数为:弹性模量E=2×1011Pa,密度ρ=7 850 kg/m3,泊松比v=0.3,长L=0.3 m、宽B=0.06 m、厚H=0.01 m。根据式(4)可得其前6阶的固有频率如表1所示;根据式(5)的振型函数可得其前6阶模态振型如图2所示。

表1 固有频率理论值与仿真值Tab.1 Theoretical and simulation values of the natural frequency

(a) 1阶振型
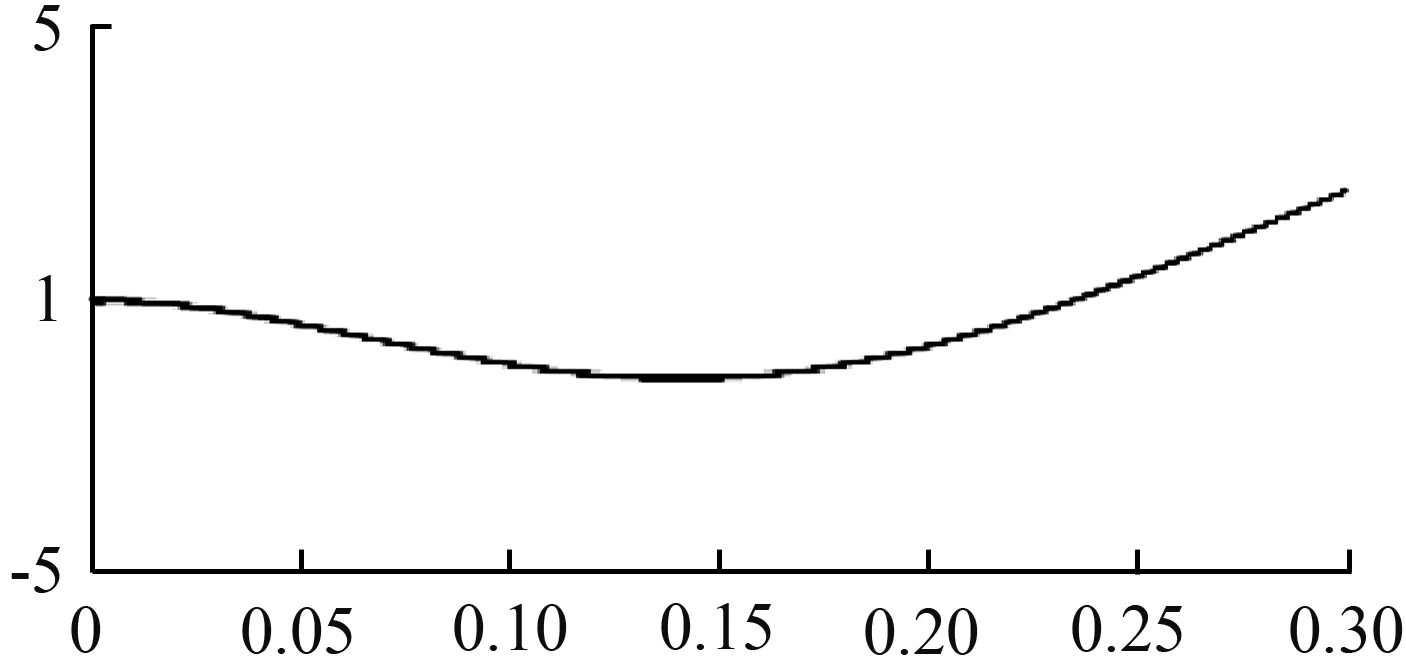
(b)2阶振型
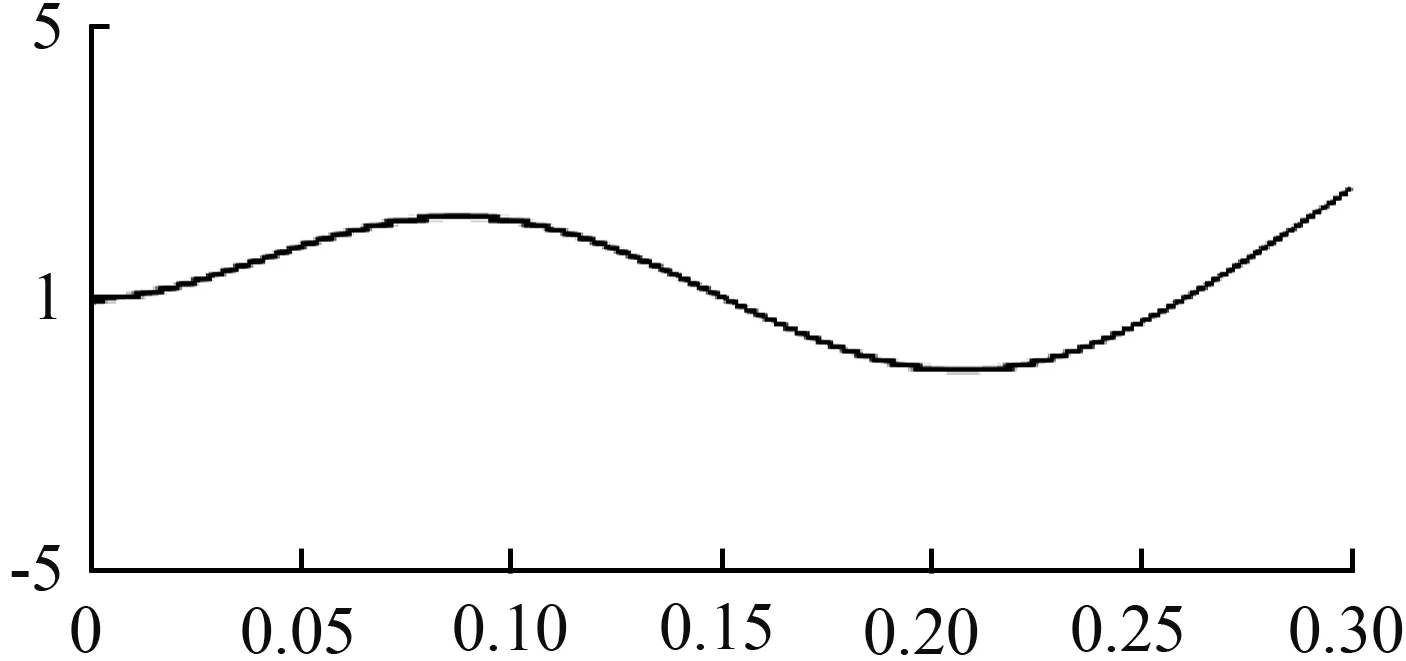
(c) 3阶振型

(d) 4阶振型
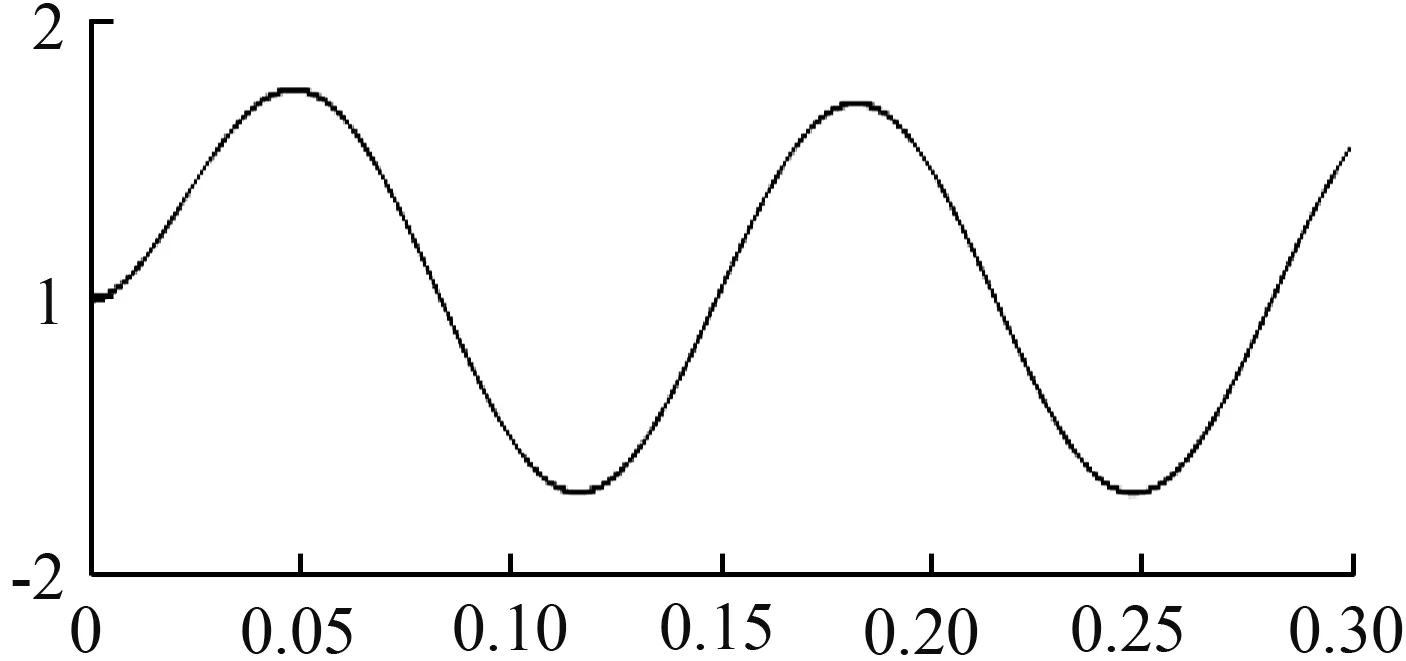
(e) 5阶振型

(f) 6阶振型
图2 理论的模态振型
Fig.2 Theoretical modal shapes
2 悬臂梁固有频率及模态振型的仿真计算
基于欧拉—伯努利梁理论计算时悬臂梁约束端是完全固定的,故在ANSYS-workbench有限元计算中设置一样的约束条件,在SolidWorks中建立悬臂梁三维模型并存为后缀名为.x_t的格式导入到Workbench的Modal模块中,设置模型的材料属性,在模型的左端面添加固定约束(fixed support),在网格划分后进行求解,得到的前6阶仿真的固有频率见表1,对应的前6阶模态振型如图3所示。
由图2和图3可知理论分析和有限元仿真分析的悬臂梁模态振型一致,且由表1可知固有频率的相对偏差很小,前6阶固有频率值最大相对偏差率只有4.15 %,说明在ANSYS-workbench软件中对悬臂梁进行模态分析是可行的。

(a) 1阶振型

(b)2阶振型

(c) 3阶振型

(d) 4阶振型

(e) 5阶振型

(f) 6阶振型
图3 仿真的模态振型
Fig.3 Simulated modal shapes
3 接触面的接触刚度与摩擦系数对悬臂梁固有频率的影响
接触对结构振动特性的影响十分复杂,不仅直接影响结构的动态服役性能,而且影响结构振动信号的幅度、频率和相位等信息。尤其是机械结构,由于机械接触面的复杂性和多样性,模态分析技术是了解结构振动特性的一个重要手段。本节从接触面的接触刚度和摩擦系数两个因素对有安装接触面的悬臂梁进行模态分析,研究接触面的接触刚度和摩擦系数对其固有频率的影响。建立如图4所示的有接触面的悬臂梁模型,悬臂梁本体呈阶梯型,悬臂梁外伸部分的各参数与上述理论和仿真分析一致,左端固定块的材料属性和悬臂梁本体部分一样,悬臂梁左端阶梯部分内嵌于固定块。

(a) 装配模型

(b) 网格模型
图4 有安装接触面的悬臂梁模型
Fig.4 Cantilever beam model with installation contact surfaces
在ANSYS-workbench中对固定块所有的竖直面添加固定约束(fixed support),由于本文主要考虑平面内的弯曲振动,故只在接触区域的上下两表面建立考虑摩擦因素(frictional)的接触对,竖直方向上不建立接触对。设置好材料属性及约束关系后进行网格划分(此处固定块和悬臂梁本体的网格大小相等),求解时采用罚函数法(pure penalty)进行求解,所谓罚函数法是用一个理想存在的接触“弹簧”,在两个面间建立接触关系,弹簧刚度称为惩罚参数或接触刚度。当面分开时,即接触面的上下层接触单元处于分离状态,弹簧不起作用;当面开始闭合时,即接触面的上下层接触单元处于穿透状态,弹簧起作用,整个过程如图5所示。弹簧偏移量△满足平衡方程:
F=kΔ,
(6)
式中,k是接触刚度,在软件程序中接触刚度通过法向接触刚度系数FKN与下层单元的刚度获得,见式(7):
k=FKN·k下层。
(7)
故在分析时通过改变接触面的法向接触刚度因子FKN来调整接触面的接触刚度k。

(a) 接触面分离

(b) 接触面穿透

(a) 1阶振型

(b)2阶振型

(c) 3阶振型

(d) 4阶振型

(e) 5阶振型
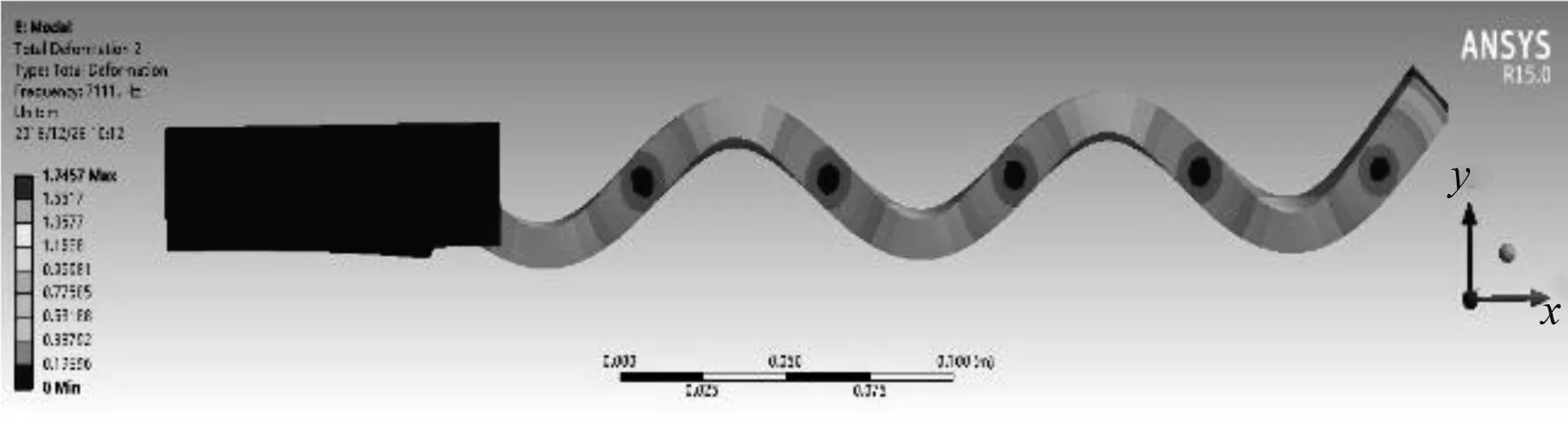
(f) 6阶振型
图6 有安装接触面的悬臂梁模态振型
Fig.6 Modal shapes of cantilever beams with installation contact surfaces
3.1 接触刚度对固有频率的影响
设置悬臂梁约束端两接触面的摩擦系数f=0.1保持不变,改变接触区域上下两接触面的法向接触刚度因子FKN,保证每次分析时网格划分的数量一致,避免因网格数量不一致而对分析结果造成影响。由表2可知有安装接触面的悬臂梁各阶固有频率随着接触面法向接触刚度因子FKN的增大而增大,由式(7)可知,即各阶固有频率随着接触面接触刚度的增大而增大。

表2 f=0.1时各法向接触刚度因子对应的各阶固有频率Tab.2 Natural frequencies corresponding to the normal contact stiffness factors at f=0.1 Hz
3.2 摩擦系数对固有频率的影响
设置悬臂梁约束端两接触面的法向接触刚度因子FKN=1保持不变,改变接触区域上下两接触面的摩擦系数f,保证每次分析时网格划分的数量一致,避免因网格数量不一致而对分析结果造成影响。各摩擦系数对应的各阶固有频率如表3所示。由表3可知有安装接触面的悬臂梁各阶固有频率随着接触面摩擦系数f的增大而增大。
由图6可知有安装接触面的悬臂梁模态振型并不会发生变化,与图2、图3中悬臂梁约束端完全固定时理论和仿真分析的模态振型保持一致。对比表1与表2、表1与表3可知,悬臂梁约束端完全固定时的各阶固有频率比设置有安装接触面的悬臂梁各阶固有频率比高。这是因为对于图4所示模型的悬臂梁本体只有两个在接触区域上下两表面所建立的考虑摩擦因素接触对的约束,而在第1、2节中理论和仿真分析时建立的约束端是完全固定的约束,当接触刚度或者摩擦系数变大时,悬臂梁约束端受到的约束力越大。造成的约束条件强度提高从而引起等效刚度增大的效应,故其各阶固有频率相应地变大。由上述分析可知,本文对有安装接触面的悬臂梁在ANSYS-workbench中的模态仿真分析结果是符合实际工程情况的,对工程应用中悬臂梁结构的设计与优化有一定的指导作用。

表3 FKN=1时各摩擦系数对应的各阶固有频率Tab.3 Natural frequencies corresponding to the normal contact stiffness factors at FKN=1 Hz
4 接触刚度对固有频率影响的实验研究
实验中主要研究接触刚度对有安装接触面悬臂梁固有频率的影响,实验与仿真中进行一样的变量控制,即在两个面间添加接触弹簧,通过改变弹簧的劲度系数来模拟接触刚度的改变,实验中选用5种不同劲度系数的扁弹簧来模拟两个面间的接触刚度见图7。实验模型如图8所示,把梁的一端放入两块夹具之间,从螺纹孔处放入弹簧,用螺栓拧紧从而使悬臂梁紧固,并保证每次拧紧的力大小相等。

图7 扁弹簧
Fig.7 Flat spring

图8 实验模型
Fig.8 Experimental model
为了快速地进行悬臂梁固有频率的测试,采用锤击激励的方式对悬臂梁进行激励,由于锤击激励是一种宽频激励,在低频带内用该方法可以一次性激励起系统的多阶模态。实验中将悬臂梁自由端的中点作为锤击点,悬臂梁根部的中点作为数据采集点,实验所用设备如表4所示。

表4 实验设备Tab.4 Experimental equipment
对其采集的时域信号进行FFT变换得其振动响应的频域信号,找出频域上各峰值对应的频率即悬臂梁的固有频率。图9为弹簧劲度系数K=12.75 kN/m时所采集的信号分析图,由图9可知该实验所用的冲击锤只能较明显地激起悬臂梁的前3阶模态。通过更换不同劲度系数的弹簧进行实验测试,结果如表5所示,由表5可知,有安装接触面悬臂梁的前3阶固有频率随着接触弹簧劲度系数的增大而增大。

(a) 时域信号

(b) 频域信号

表5 不同劲度系数对应的固有频率Tab.5 Natural frequencies corresponding to different stiffness coefficients Hz
5 结论
利用欧拉—伯努利梁理论和ANSYS-workbench有限元软件仿真计算悬臂梁前6阶的固有频率和模态振型,对比两者的结果可知,仿真值和理论值相对误差较小,说明在Workbench中对悬臂梁进行模态分析是可行的。在ANSYS-workbench中讨论有安装接触面的悬臂梁其接触面的接触刚度和摩擦系数对其固有频率的影响,发现有安装接触面的悬臂梁的固有频率随着接触面接触刚度和摩擦系数的增大而增大,而且还发现悬臂梁约束端完全固定时的各阶固有频率比设置有安装接触面的悬臂梁各阶固有频率高。最后建立实验模型研究固有频率随接触刚度的变化关系,其实验结果与仿真结果固有频率的变化趋势具有一致性。

