矩阵方程组异类约束解的MCG算法分析
陈世军,赖德清
(1.福建工程学院 应用技术学院,福建 福州 350001;2.福建永德吉集团股份有限公司,福建 福州350001)
在结构动力模型修正、自动控制理论等领域中会涉及矩阵方程组约束解问题。许多学者对这类约束解问题做了很多研究。比如,廖安平、Li L和柯艺芬[1-4]等建立了求单变量和双变量矩阵方程(组)同类约束解的迭代算法。冯天祥、肖庆丰、盛兴平、彭程和李敏[12-20]等研究了线性和非线性矩阵方程的约束最小二乘解问题。变形共轭梯度算法是求解矩阵方程(组)异类约束解的一种有效的方法,张凯院、武见、李书连和杨家稳[5-11]等建立了求双变量和多变量矩阵方程(组)异类约束解以及最小二乘解的迭代算法。
1 相关定义
定义1划分n阶单位矩阵I=(e1,e2,…,en),称S=(en,en-1,…,e1)为n阶次单位矩阵。若X∈Rn×n满足SXS=X,称X为中心对称矩阵。若X∈Rn×n满足SXS=-X,称X为中心反对称矩阵。若X∈Rn×n满足SXS=X且XT=X,称X为双对称矩阵。若X∈Rn×n满足SXS=-X且XT=X,称X为对称次反对称矩阵。
定义2设P∈Rn×n满足PT=P,P2=I,若X∈Rn×n满足PXP=X,称X为关于矩阵P的自反矩阵。若X∈Rn×n满足PXP=-X,称X为关于矩阵P的反自反矩阵。若矩阵X既是对称矩阵又是自反矩阵,称X为对称自反矩阵。
用Rm×n表示m×n实矩阵集合,定义同阶实矩阵A与B的内积为(A,B)=tr(ATB),矩阵的Frobenius范数。记n阶实对称矩阵、反对称矩阵、中心对称矩阵、中心反对称矩阵、自反矩阵、反自反矩阵、双对称矩阵、对称次反对称矩阵、对称自反矩阵集合分别为Ω1、Ω2、Ω3、Ω4、Ω5、Ω6、Ω7、Ω8和 Ω9。当X1∈Ω1,X2∈Ω2,X3∈Ω3,……,X9∈Ω9时 ,记(X1,X2,…,X9)∈Ω1-2-…-9,并称(X1,X2,…,X9)为约束 1-2-…-9 矩阵。
文献[5~8],本文建立求含九个未知矩阵的矩阵方程组异类约束解的迭代算法.具体讨论问题如下:
问题Ⅰ设,求 (X1,X2,…,X9)∈Ω1-2-…-9使得
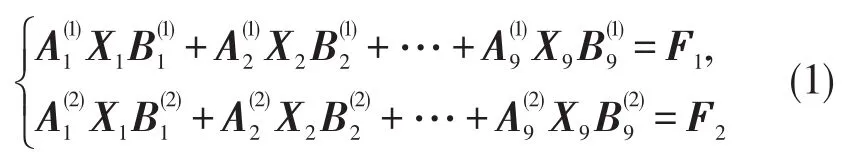
即求矩阵方程组(1)的约束解。
2 求解问题Ⅰ的迭代算法
下面建立求解问题Ⅰ的修正共轭梯度法(MCG算法)如下。
引入记号:
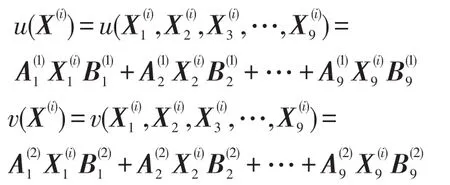

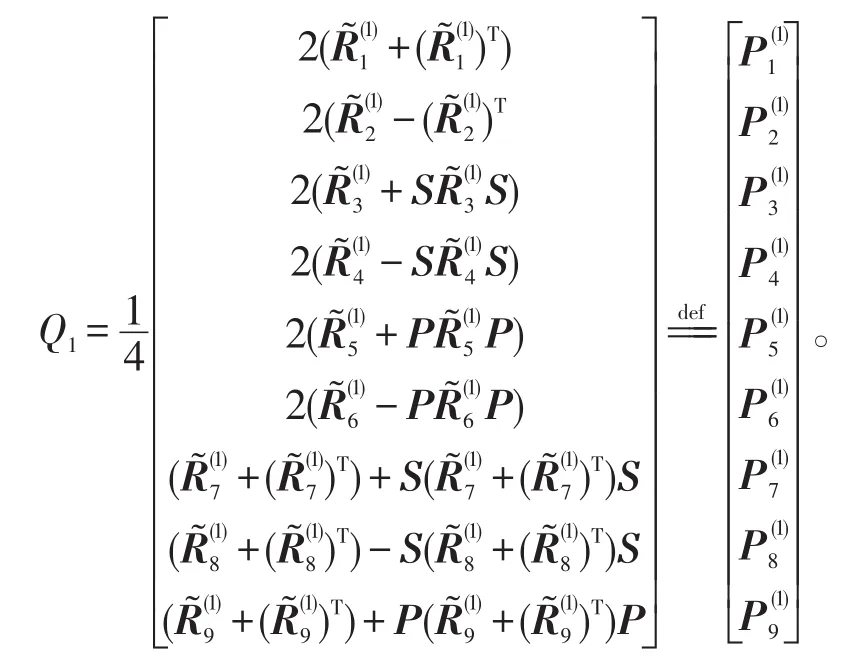
Step 3:计算

如果Rk=0,或者Rk≠0而Qk=0,停止计算;否则,置k:=k+1,转第2步。
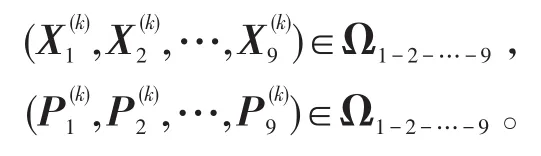
下面给出MCG算法的基本性质和定理,证明MCG算法在有限步计算之后停止。具体证明过程文献[8]。
引理1对任意的A∈Rn×n,(X1,X2,…,X9)∈Ω1-2-…-9都有

性质1对于MCG算法中的矩阵Ri,Qi和,有

性质2设k≥2,对MCG算法中的矩阵Ri和Qi,有

性质3设是问题Ⅰ的任意一组约束解,那么对任意初始矩阵,由 MCG 算法得到的矩阵Rk,Xi(k)和Qk满足

定理1设问题Ⅰ有约束解,则对任意的初始矩阵,MCG 算法可在有限步计算后求得问题Ⅰ的一组解。问题Ⅰ不相容的充要条件是在MCG算法中存在某个正整数,使得Rk≠0而。
为了书写方便,引进下面的矩阵函数
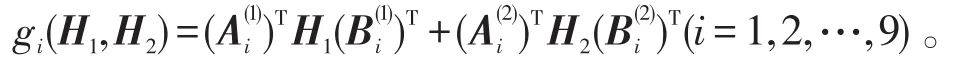
定理2若问题Ⅰ相容,对任意矩阵H1,H2∈Rn×n,选取初始矩阵满足

则MCG算法可在有限步计算后得到问题Ⅰ的唯一极小范数解,即矩阵方程组(1)的唯一极小范数约束解。
3 数值算例
用本文建立的MCG算法求矩阵方程组(1)的一组约束解,这里取当X1∈Ω1,X3∈Ω3,X5∈Ω5,X9∈Ω9时 ,记 (X1,X3,X5,X9)∈Ω1-3-5-9,并 称(X1,X3,X5,X9)为约束1-3-5-9矩阵。方程组(1)可以写成下面方程组
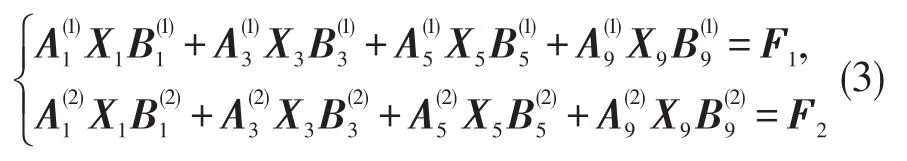
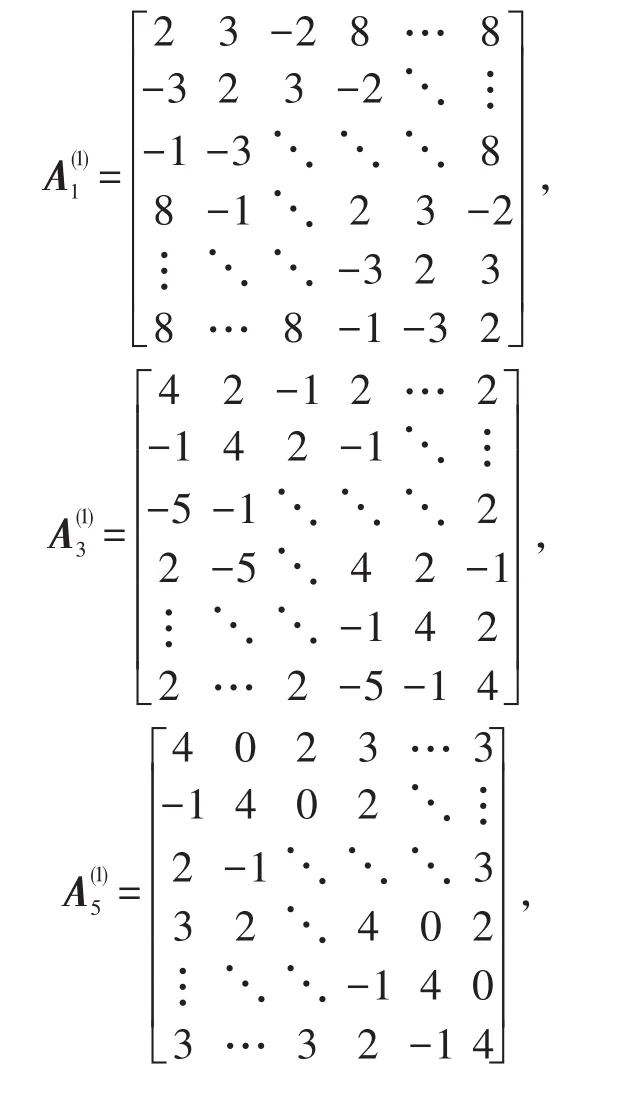
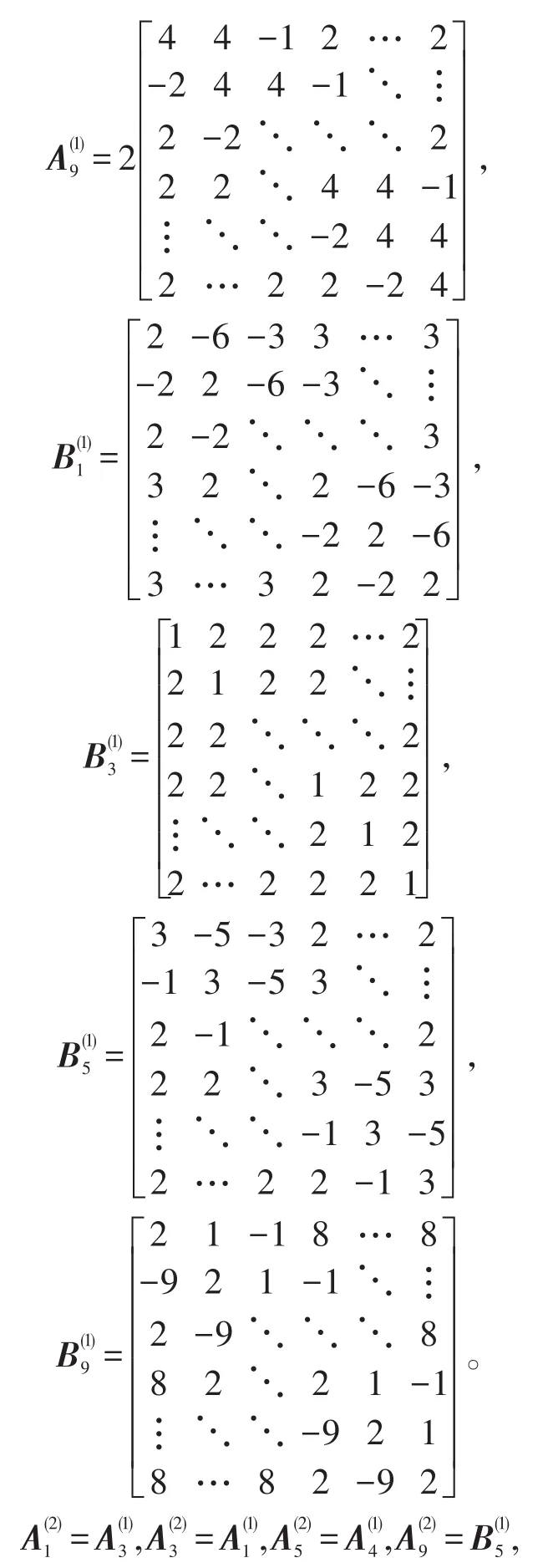
求矩阵方程组(3)的1-3-5-9解和极小范数约束1-3-5-9解,其中

X0=-3(xij)4n×4n,X1=2(xij)4n×4n,xij=1,ε=10-10(终止准则)。
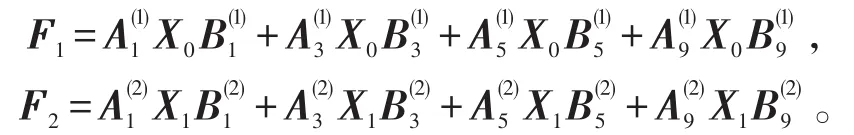
(ⅱ)(在式(2)中取H1=H2=(aij)4n×4n,aij=1),选取初始约束1-3-5-9矩阵,按照MCG算法可求得矩阵方程组(3)的极小范数约束1-3-5-9解,计算结果如表2。
4 小结
本文建立的求含有多个特殊矩阵的矩阵方程组异类约束解的迭代算法(修正共轭梯度法MCG),该算法是在求线性矩阵方程组同类约束解的迭代算法基础上,将MCG算法推广到矩阵方程组异类约束解。给出了算法的性质和定理,判断了算法能在有限步收敛,同时给出在初始矩阵取特殊矩阵时,矩阵方程组可以得出极小范数解。数值算例给出了约束1-3-5-9解和极小范数1-3-5-9解,算例表明该算法是可行的,同时,数值算例表明,随着矩阵方程的阶数增加,迭代次数会增加,解矩阵的范数和逼近误差也会增大。通过增加矩阵方程组中矩阵变量的个数和方程的个数,采用类似的方法,可以建立求矩阵方程组的其他异类约束解的迭代算法。

表1 约束1-3-5-9解的计算结果

