基于改进TCAR的高精度定位技术研究

曹 兢，薛晓琴



基于改进TCAR的高精度定位技术研究

曹 兢，薛晓琴

（北京航天长征飞行器研究所 北京 100076）

模糊度解算是实现快速、高精度定位的关键，一直是全球卫星导航系统研究的热点。北斗系统提供三频信号，可以进行不同形式的组合，实现高精度定位和模糊度解算。通过分析现有的无电离层三频模糊度解算方法（TCAR）和组合观测值的噪声特征，提出一种低噪声无电离层影响的宽巷与IF组合相结合的TCAR算法，选取低噪声长波长的宽巷组合观测值，在几何模型下用最小二乘法逐级解算模糊度，最终实现静态定位。为了验证组合噪声的影响和各种TCAR算法的性能，对北斗中基线的实测数据进行实验，并且比较提出方法与现有算法的模糊度解算情况及位置精度。结果表明，提出方法可以有效提高模糊度解算的成功率，实现高精度定位。

高精度定位；三频模糊度解算；低组合噪声；无电离层影响

引 言

高精度定位逐渐成为全球导航卫星系统（GNSS）的研究热点，而精密定位技术依赖于载波相位模糊度的成功解算，传统的单频和双频模糊度解算并不能满足高精度定位的需求。随着GNSS多频率载波信号的开通，对多频信号观测值的研究越来越多，研究发现组合多频信号观测值可以提高快速模糊度解算的成功率和定位精度。

本文分析组合噪声特征，在现有GF-TCAR方法[8]和无电离层组合方法[7]的基础上，提出了无电离层影响的宽巷与IF组合相结合的TCAR算法，逐级解算模糊度，并且加入电离层未知参数。考虑到不同基线长度下的误差影响不同，在中基线情况下，对北斗B1（1561.098MHz）、B2（1207.140MHz）、 B3（1268.520MHz）信号的组合观测值进行处理。最后，为了验证新方法的性能，进行整型模糊度的Ratio值检验、电离层延迟参数计算和原始模糊度成功率的统计。

为表示方便，标记传统的TCAR方法为Algorithm-A，无电离层组合方法为Algorithm-B，本文改进的无电离层模糊度解算方法为Algorithm-C。

1 组合观测值的基本模型和特征

1.1 基本观测模型

组合双差伪码和相位观测值[5]是对三频信号进行线性组合，可以表示为

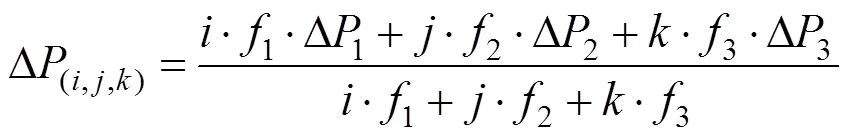
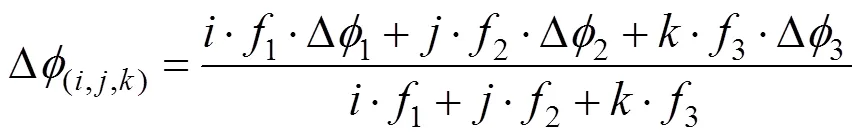
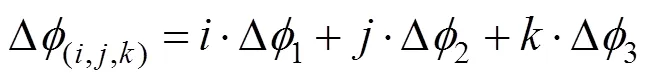
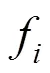
组合频率、对应的波长和整型模糊度定义为

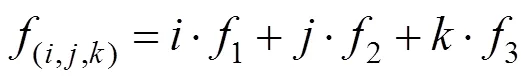
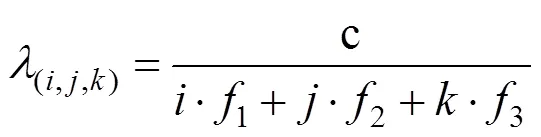
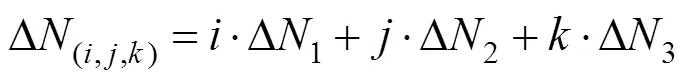
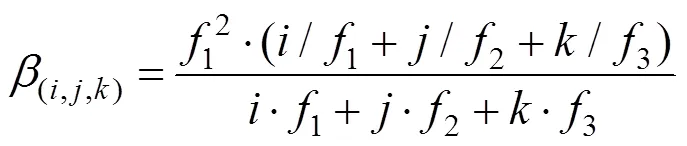
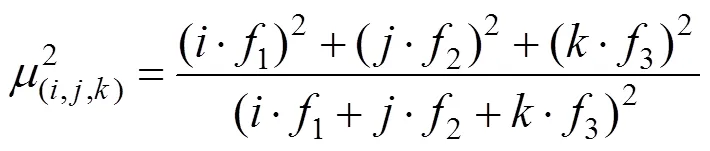
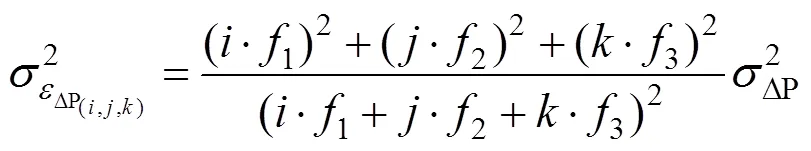
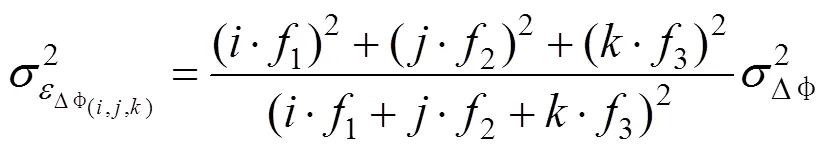
组合双差伪码和相位观测值的方程式为

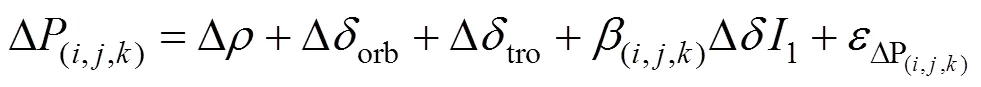
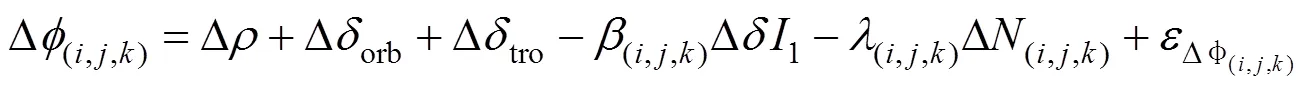
根据相位观测值的模型，总体相位噪声程度（以米为单位）可以定义为

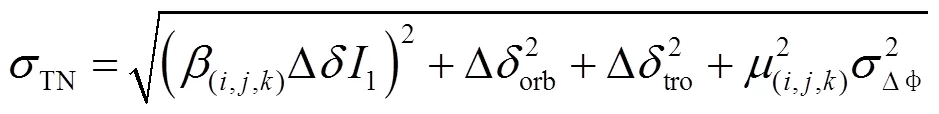
1.2 北斗三频观测量及组合特征

表1是本文对误差因子的估算。在此基础上计算出常用超宽巷和宽巷组合信号的噪声特征，如表2所示。

表1 短基线和中基线的双差噪声估算

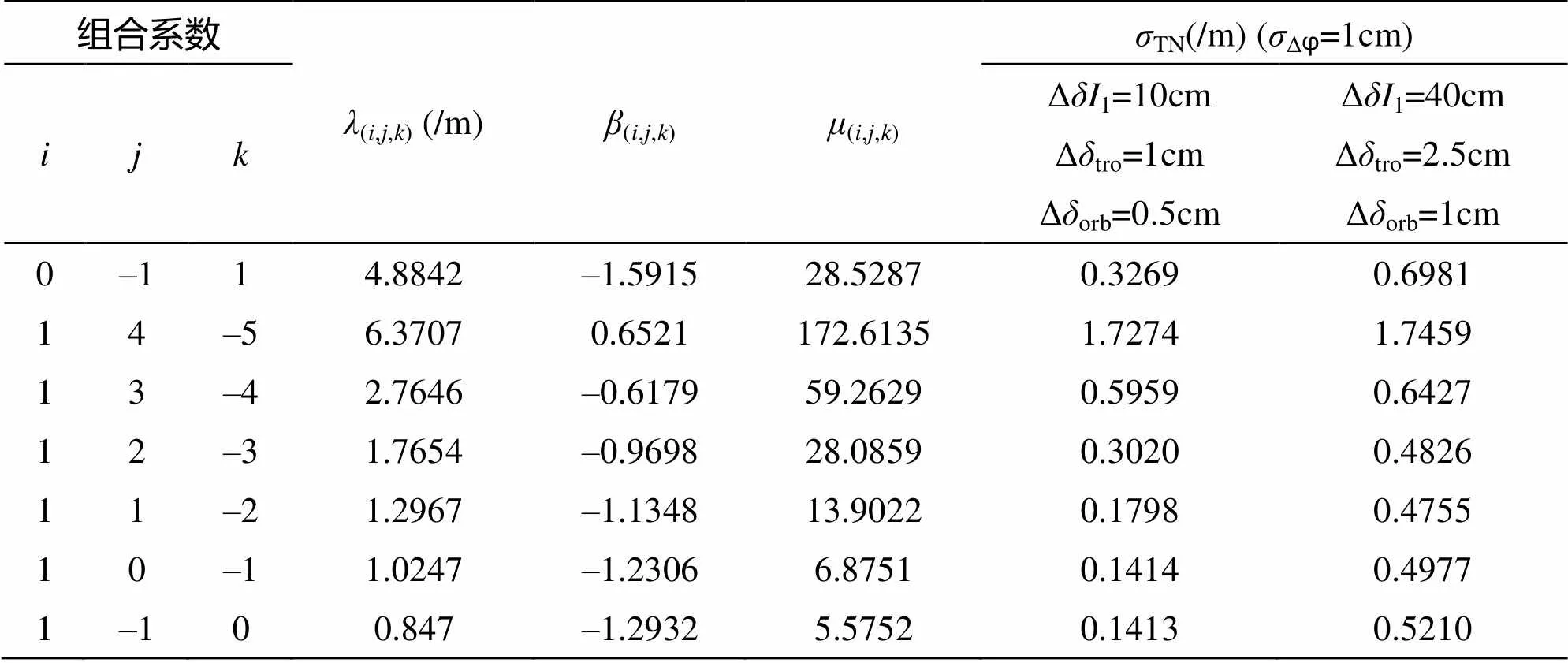
表2 北斗三频信号的超宽巷/宽巷组合特征

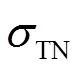
2 传统TCAR方法（Algorithm-A）

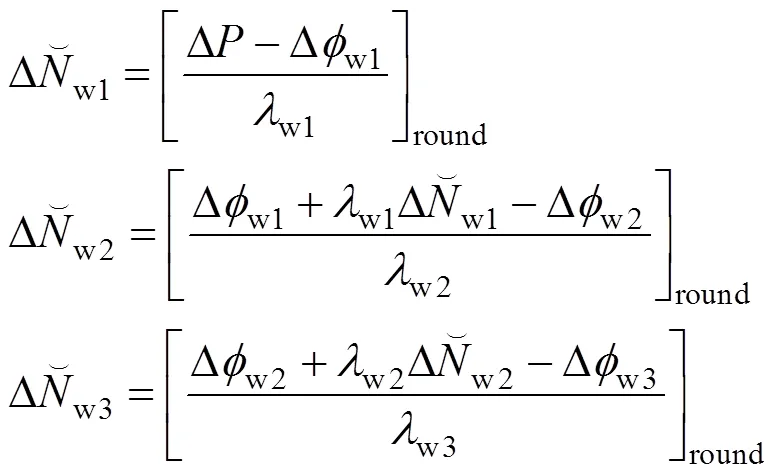
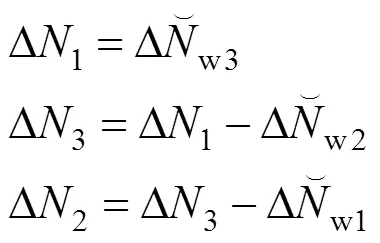
通过窄巷模糊度与宽巷模糊度的线性关系（式（15））解算出三频信号的原始模糊度。

3 无电离层TCAR方法（Algorithm-B）

Tang[7]对超宽巷（0,–1,1）、宽巷（1,0,–1）和（1,–1,0）、窄巷（1,0,0）组合应用无电离层的三频模糊度算法，本文选取超宽巷（0,–1,1）和（1,4,–5）组合、宽巷（1,2,–3）和（1,1,–2）组合对该算法进行介绍。

3.1 超宽巷模糊度解算

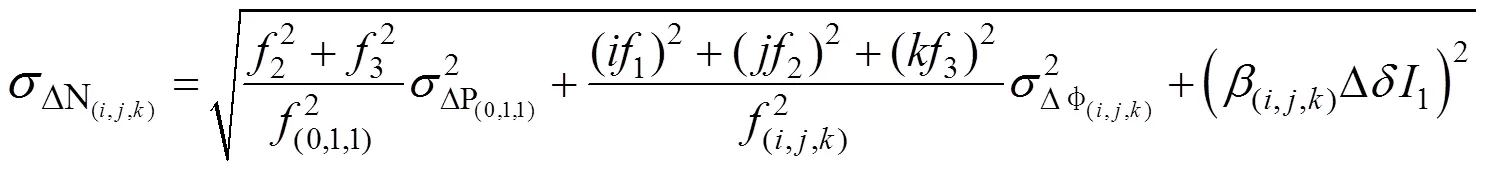
3.2 宽巷模糊度解算

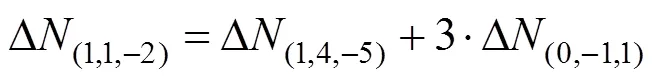
3.3 窄巷模糊度解算

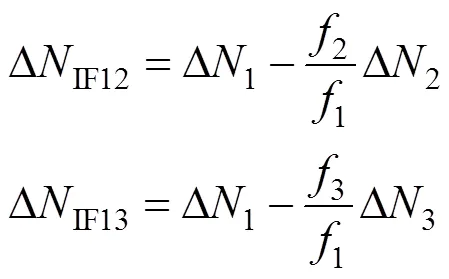
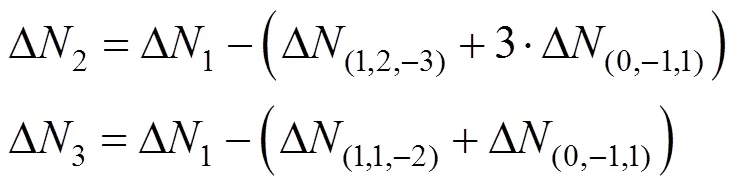
根据窄巷与超宽巷、宽巷模糊度的关系（式（22）），式（21）可转换为

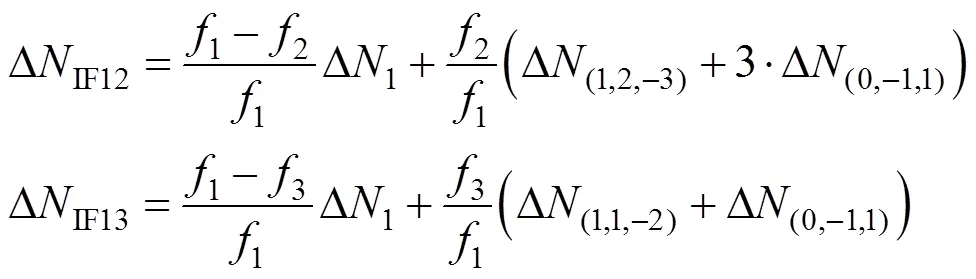
窄巷模糊度观测方程如下

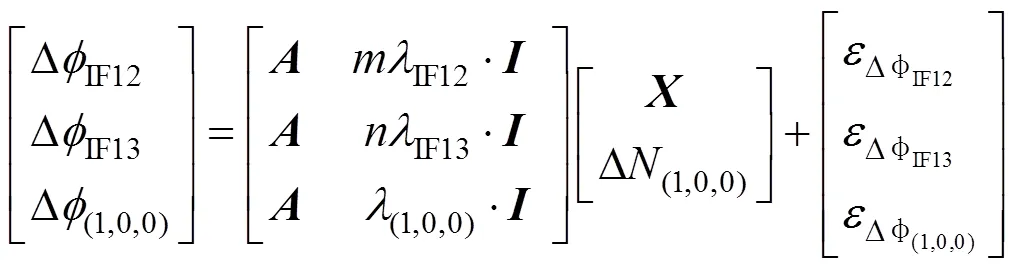
4 改进的无电离层TCAR方法（Algorithm-C）

由于基线较长时误差较大，双差并不能消除大部分电离层延迟，而且传统的TCAR方法未考虑电离层的影响。本节在现有的无电离层方法Algorithm-B基础上，提出改进的无电离层误差的三频模糊度算法algorithm-C。在几何模型下，基于最小二乘准则，逐步求解模糊度，并作为高精度观测值代入下级使用。超宽巷和宽巷模糊度解算步骤与第3节方法相同。

本方法考虑电离层延迟对宽巷WL和窄巷NL模糊度的影响，利用已经解算的宽巷模糊度，将无电离层影响的IF组合与宽巷WL组合相结合，同时加入电离层参数，得到窄巷模糊度观测方程，如式（25）所示。

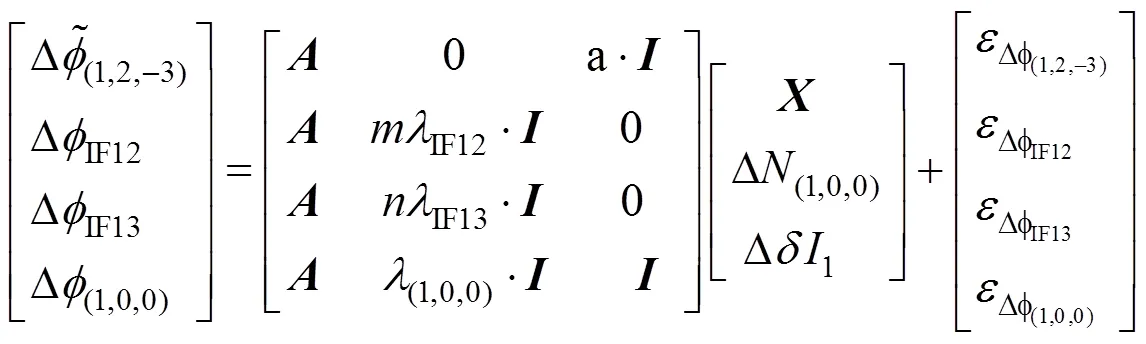
5 实验分析

5.1 采集数据分析

本文介绍的算法都是单个历元独立解算模糊度，对浮点模糊度使用LAMBDA算法进行整型固定。我们采用Ratio-test检测，阈值设为2，当Ratio值大于阈值2时，认为可以接受该整型模糊度。

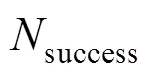
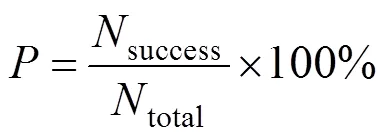
为了验证三种三频模糊度解算方法的可靠性，本文采用Trimble NetR9接收机采集两个测站XBGD和HTTH的数据。对26.3km中基线情形，取同一段时间的北斗B1、B2、B3信号观测值，分别在Condition-1和 Condition-2两种条件下，对三种TCAR方法进行实验分析。实验中，截止仰角取10°，选取仰角最大的卫星作为参考卫星。

表3给出了26.3km中基线的实验数据信息，同时采集0点到20点共20个小时的北斗数据。

表3 中基线的实验数据信息

图1显示了中基线Day180在实验阶段的可见卫星数SV与空间精度因子PDOP值， PDOP值越小，表明卫星的空间几何分布情况越好，可以看出所有的PDOP值基本都在3以下。

图2展示了Algorithm-C算法求出的双差电离层延迟，从图中统计的RMS值可以看出，中基线的电离层延迟引起的噪声在8cm以内。

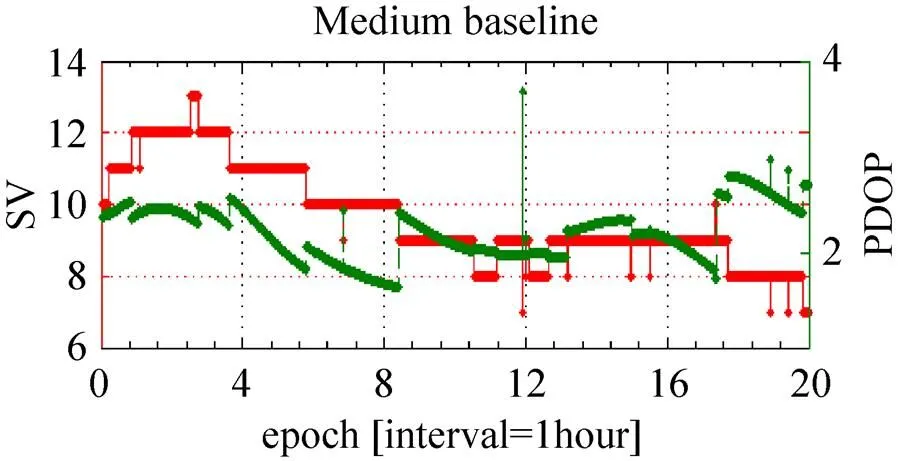
图1 可见卫星数和PDOP值

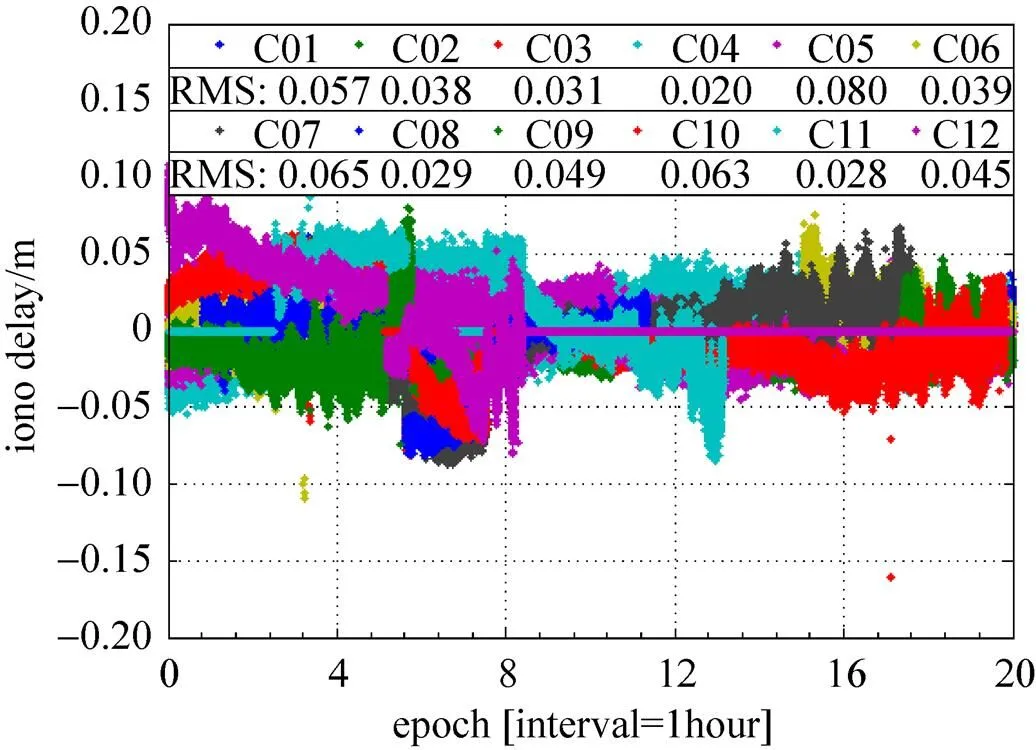
图2 中基线下的电离层延迟

图3显示了对式（25）计算的浮点模糊度应用LAMBDA方法时的Ratio-test值。可以看出，对于中基线，Condition-1条件和Condition-2条件下的所有Ratio值都大于阈值2，所以LAMBDA算法固定的整型值可以被接受。

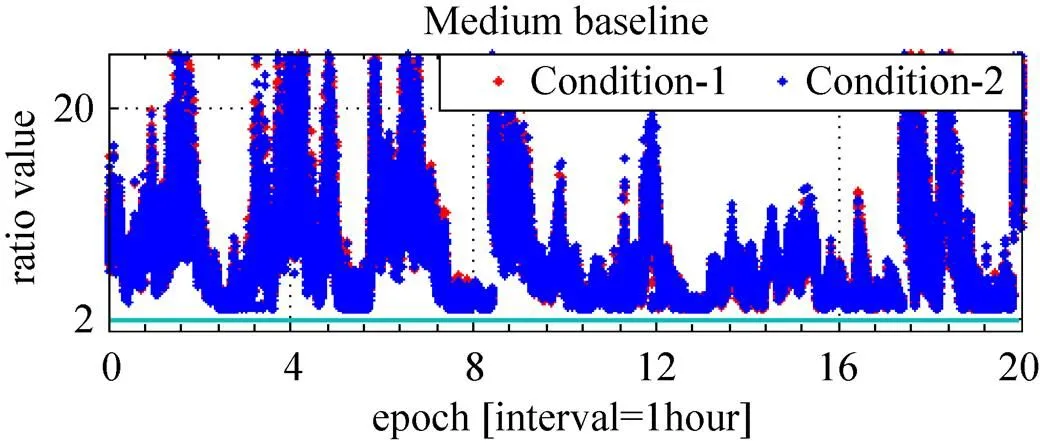
图3 模糊度检测值

5.2 中基线实验结果

图4是对中基线Day180采用三种TCAR方法解算的位置误差。表4总结了三种TCAR算法在东北天（ENU）方向的位置误差均方根值（RMS）。表5统计了不同TCAR方法解算的原始模糊度成功率。

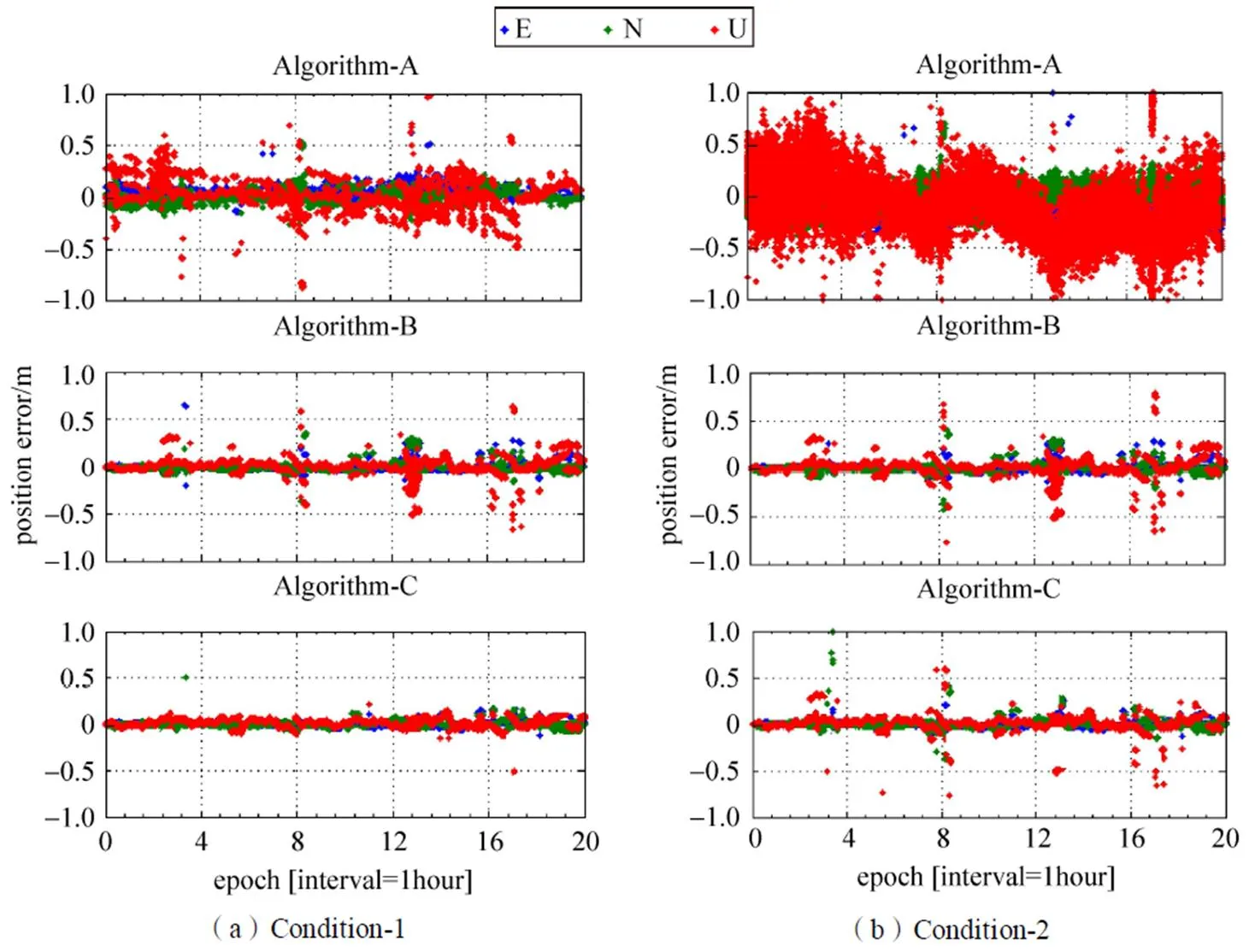
图4 东北天方向上的定位误差

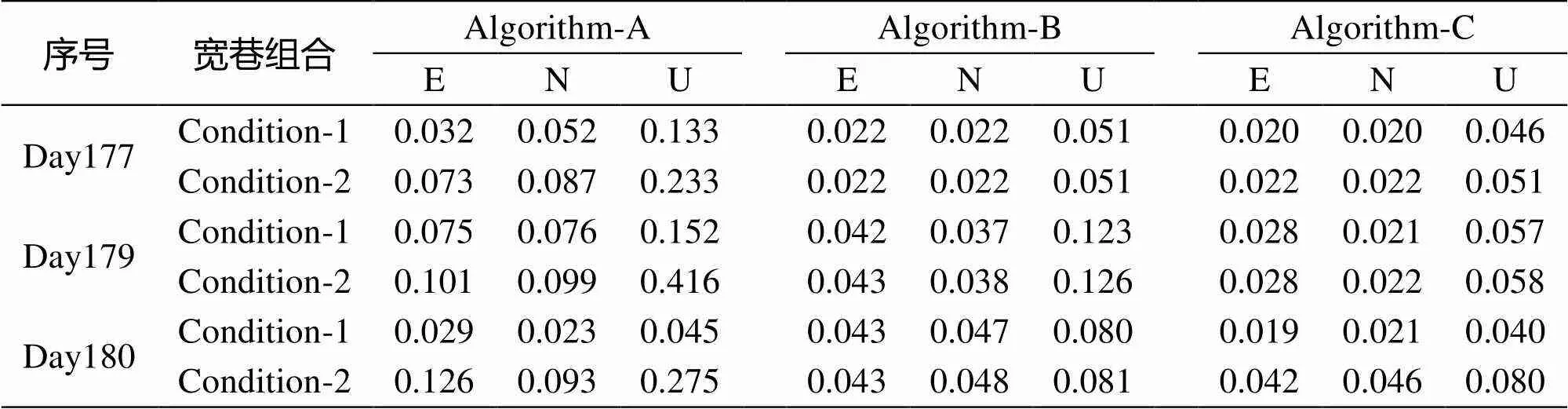
表4 中基线的定位精度RMS值（单位：m）

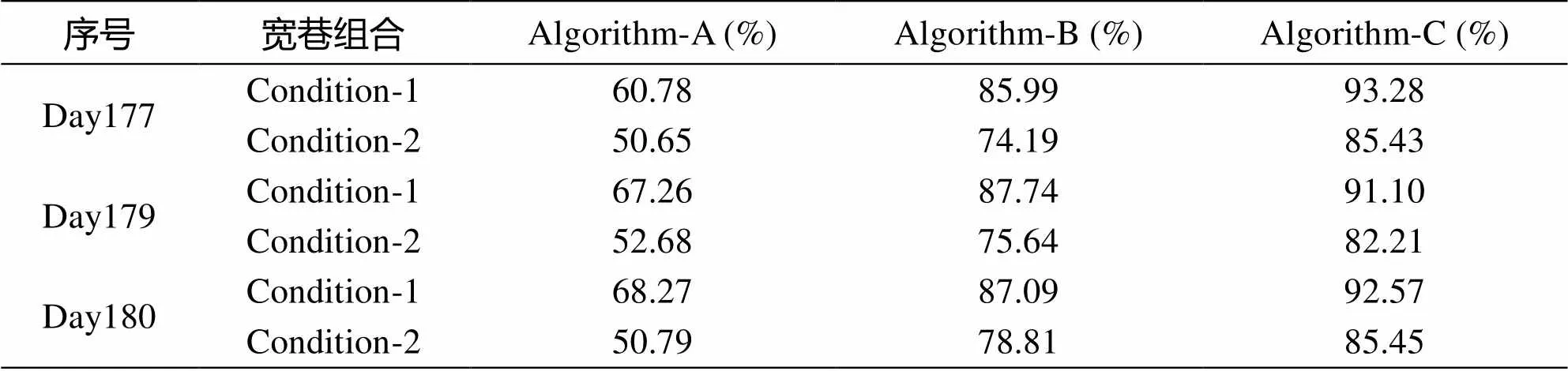
表5 模糊度解算成功率

可以看出，当选取Condition-2的宽巷组合时，Algorithm-A算法的定位精度很差，模糊度解算成功率也只能达到50%；而两种不同组合条件对Algorithm-B算法的性能影响基本相同。从表2的中基线组合噪声可以看出，理论上Condition-1和Condition-2的组合噪声程度相近，但由于Condition-2下B1、B2、B3信号的噪声同时被引入，在实际中这对三种TCAR算法的效果都有不同程度的影响。本文提出的算法Algorithm-C计算出了厘米级的电离层时延参数，提高了定位精度，在Condition-1条件下解算的原始模糊度成功率能够达到90%以上，性能优于Algorithm-A和Algorithm-B。

6 结束语

本文在理论上分析了组合观测量的主要误差源，选取最佳的超宽巷组合（0,–1,1）和（1,4,–5），比较了Condition-1和Condition-2的宽巷组合噪声。在无电离层TCAR算法基础上，提出了IF组合与WL组合相结合的算法Algorithm-C，并加入电离层延迟参数来解算模糊度。在中基线情形下，通过实验分析组合噪声对算法的影响，以及三种TCAR算法的性能差异，结论如下：

①实验结果与理论分析相符，在中基线下，由于Condition-2的线性组合同时引入了三个频率信号的噪声，所以Condition-1是噪声较小的最佳组合。

②传统的Algorithm-A算法可靠性较低，仅适用于短基线情形。Algorithm-B算法性能较优，中基线下模糊度解算成功率能够达到85%以上。相比较而言，本文提出的Algorithm-C算法性能最好，能够提高模糊度的解算成功率到90%以上，并且实现了中基线情形下厘米级的定位精度。可见，本文提出的Algorithm-C算法适用于中基线情形下的模糊度解算。

[1] FORSSELL B, MARTIN N M, HARRIS R A. Carrier phase ambiguity resolution in GNSS-2[C]//10th International Technical Meeting of the Satellite Division of ION, Kansas City Missouri, 1997: 1727–1736.

[2] HATCH R, JUNG J, ENGE P , et al. Civilian GPS: the benefits if three frequencies[J]. GPS Solut, 2000, 3(4): 1–9.

[3] JI S, CHEN W, ZHAO C, et al. Single epoch ambiguity resolution for galileo with the CAR and LAMBDA methods[J]. GPS Solut, 2007, 11(4): 259–268.

[4] TEUNISSEN P J G. The least-squares ambiguity decorrelation adjustment: a method for fast GPS integer ambiguity estimation[J]. Journal of Geodesy, 1995, 70(1-2): 65–82.

[5] FENG Y. GNSS Three carrier ambiguity resolution using ionosphere-reduced virtual signals[J]. Journal of Geodesy, 2008, 82(12): 847–862.

[6] FENG Y, RIZOS C, HIGGINS M. Multiple carrier ambiguity resolution and performance benefits for RTK and PPP positioning services in regional areas[C]//20th International Technical Meeting of the Satellite Division of ION, 2007: 668–678.

[7] TANG Weiming, DENG Chenlong, SHI Chuang, et al. Triple-frequency carrier ambiguity resolution for beidou navigation satellite system[J]. GPS Solut, 2014, 18: 335–344.

[8] ZHANG Xiaohong, HE Xiyang. Performance analysis of triple-frequency ambiguity resolution with BD observations[J]. GPS Solut, 2016, 20: 269–281.

[9] CHEN Dezhong, YE Shirong. A geometry-free and ionosphere-free multipath mitigation method for BDS three-frequency ambiguity resolution[J]. Journal of Geodesy, 2016, 90: 703–714.

Research on high precision positioning technology based on improved TCAR

CAO Jing, XUE Xiaoqin

（Beijing Institute of Space Long March Vehicle, Beijing 100076, China）

Ambiguity resolution is the key to achieve rapid and accurate positioning, which is always the focus of GNSS research. The Beidou navigation system provides triple-frequency signals, which can be combined into different forms. Based on these combinations, we can realize precise positioning and fix the ambiguity. In this paper we analyze the noise characteristics of combined observations and current ionosphere-free three carrier ambiguity resolution (TCAR) algorithms. Then we propose a TCAR algorithm with low noise and ionosphere-free impact, which is processed by the least squares principle under geometry model. After that, we achieve static positioning. Finally in order to verify the noise effect of combination and the performance of TCAR algorithms, a series of tests are conducted on real observations in medium baseline. What is more, comparisons are made between current algorithms and the proposed algorithm. The results indicate that the proposed TCAR algorithm can improve ambiguity resolution success rate effectively and achieve precise positioning reliably.

Precise positioning; TCAR; Low combined noise; Ionosphere-free

P228

A

CN11-1780(2019)02-0031-08

2019-01-26

2019-02-19

曹 兢 1993年生，工程师，主要研究方向为卫星导航与定位技术。

薛晓琴 1992年生，硕士，工程师，主要研究方向为卫星导航与定位技术。