飞行器编队网络测距技术研究

王鹏宇



飞行器编队网络测距技术研究

王鹏宇

（中国电子科技集团公司第二十七研究所 郑州 450047）

针对飞行器编队自主测控中的网络测距问题，在通过TDMA方式实现网络通信的同时，完成高精度时频同步与测距功能，测距精度可达厘米级。详细论述网络测距的基本原理，对测距误差展开分析，并在此基础上讨论网络测距功能与网络协议的关系。

飞行器编队；网络；星间测距

引 言

编队飞行小卫星在科学实验、近地勘测、深空探测及干涉测量等领域起到非常重要的作用[1]。编队飞行关键技术包括编队飞行设计、相对导航、星间通信等[2]，其中相对导航与星间通信是小卫星编队任务姿态保持和星间数据交换的主要手段。相对导航主要是指测量和估算编队各星之间的相对位置、速度和姿态。由于小卫星体积较小、轨道较低，利用力学模型对其定轨，精度不会很高[3]。广泛采用的有效测控方法是对编队中一颗参考星进行精确定位，编队其他卫星在参考星状态量基础上，利用星间通信链路获得卫星相互间的距离信息，通过联合解算，求得小卫星的位置状态量[4]。星间通信一般参考地面网络协议并加以适应性改造。例如，静态星座常采用HDLC协议、CCSDS Proximity-l协议；属于动态星间通信的小卫星编队常采用竞争类MAC协议，如对IEEE 802.11协议的各种改进，或者非竞争类MAC协议，如TDMA等。在网络层方面一般参考自组织网络技术[5,6]。

与小卫星编队测控类似，无人机编队同样面临着通过机间测距完成编队姿态保持，以及编队组网问题[7-9]。由于通信网络与飞行器测控属于不同的技术领域，所以飞行器编队组网分析很少考虑测控需求，仅仅将编队成员视为网络数据通信节点，飞行器所特有的高动态性是此类网络的研究重点[10,11]。当引入测控需求后，飞行器编队组网技术不但要考虑网络的数据交换性能，还要考虑网络传输对编队整体测控性能的影响。

不论小卫星还是无人机编队测控，高精度距离测量都是编队整体姿态控制所需的主要观测量。本文在文献[12]基础上，将星间测距扩展至飞行器编队网络，给出了高精度网络测距（厘米级）的基本原理，对误差进行了分析，并讨论了网络测距功能对通信协议造成的影响。

1 传统的编队飞行器测控方式

图1给出了传统的飞行器编队测控方式。

如图1所示，为了实现对编队中所有成员的测控，下行遥测可以采用基于多波束相控阵天线的空分多址（SDMA）、基于时隙划分的时分多址（TDMA）、基于伪码的码分多址（CDMA）、基于频率分开的频分多址（FDMA）以及它们的组合。上行遥控则采用相应的信道复用方式（S/T/C/FDD）。在测控的同时，一般利用伪码序列完成测速、测距。

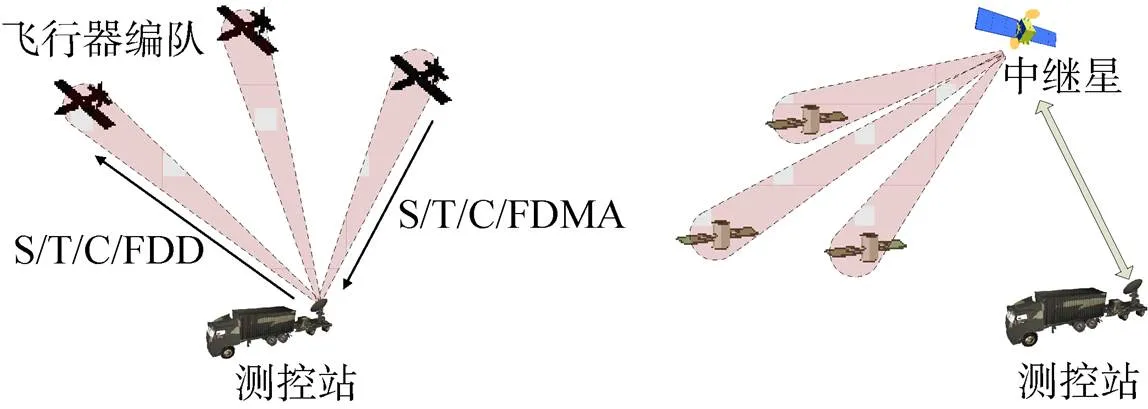
图1 传统的飞行器编队测控方式

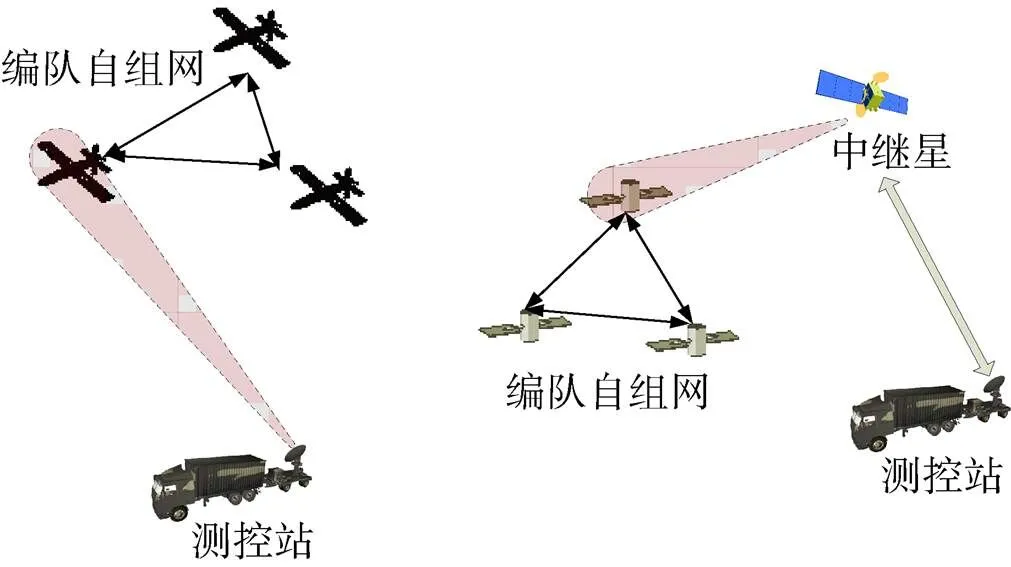
图2 飞行器编队自主测控

传统编队测控本质上还是测控站对单一飞行器的测控，即测控站须对编队成员分别测控。这种测控方式对小卫星编队来说，若采用地面测控方式则存在着测量弧段较短和测量目标较多的难点[13]，若采用中继星测控方式则测控资源有限，很难满足所有编队任务的需求；而对无人机编队来说，不论是地面测控还是中继星测控，当出现通信时延或中断时，极易造成编队失控，所以必须提高编队自主测控能力。

图2给出了飞行器编队自主测控示意图。根据飞行器编队任务特点，地面测控系统只对编队中位置参考成员进行精确测控，编队中其他成员通过成员间通信链路实现距离测量，根据参考成员状态信息、编队队形设定和距离测量值，编队成员按照一定算法自行调整自身状态[4,14]。同时，各成员的测控信息通过编队自组网中的参考成员与地面测控站进行交换。

2 网络测距基本原理

网络测距是编队自主测控的基础，本节将详述网络测距的基本原理。

网络测距属于高精度时频同步，通过微波双向对传时间基准信号完成测距及时间同步。在一般测控系统中，测距双方向对方发送与本地时钟同源的基准伪随机序列，通过直序扩频与低速测控数据复用，数据中含有测距特征信号，特征信号由数据域中通信双方约定字段给出（如某一特定位置1），且测距特征信号与星载定时脉冲同步，因此要求数传符号时钟与本地基准时钟同源。

在以往点对点测控方式中，测控双方分别独享上下行测控链路，双向对传测距时间同步可以同时进行，而网络测距要求在网络通信的同时完成测距任务，这就需要考虑共享链路情况下时钟传递问题。如图3所示，我们以TDMA网络接入方式为例，假设在一个时隙帧中节点A时隙与节点B时隙相隔1个时隙，节点B时隙与下一时帧的节点A时隙相隔2个时隙。

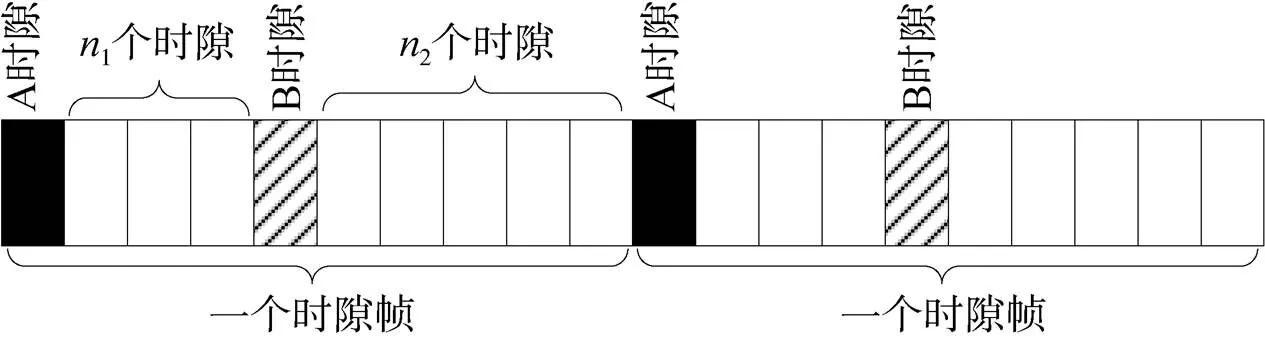
图3 TDMA时隙划分

约定所有数据传输帧在一个时隙内完成收发，最大传输距离由数据帧的传输保护间隔决定，即A节点发出的传输帧将在A时隙内被最大传输距离范围内所有节点接收完毕。根据双向测距原理，测距双方必须将自己测量得到的时差数据通过数据帧传递给对方，时差测量取本地发出测距标志位与接收到其他节点数据帧中测距标志位时刻的本地时间差。则在TDMA方式下，一次测量时间计算如图4所示。

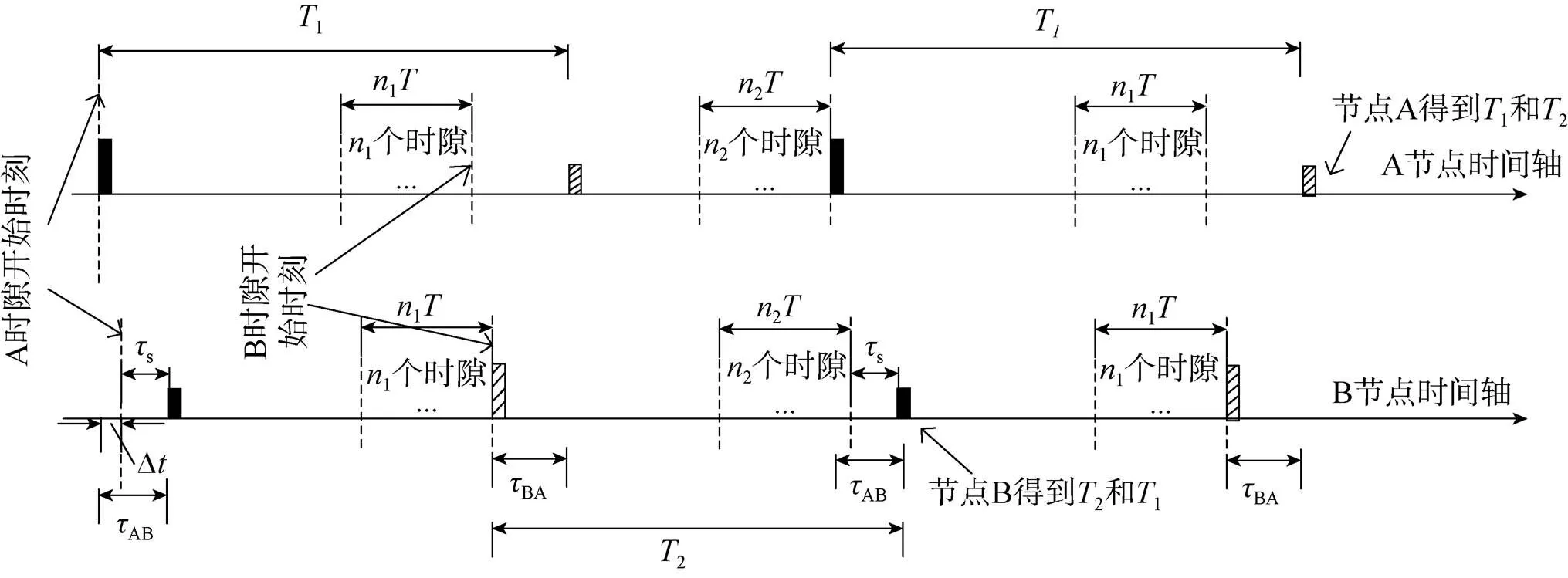
图4 A、B节点静止时测量时间计算

如图4所示，A节点在A时隙开始时刻发出数据帧（为简单起见，暂不考虑系统零值和节点运动，并假设测距标志位与时隙开始时刻对齐），则经过AB传输延时，传递到节点B，图中s为节点B测得的A数据帧测距标志位距节点B时间轴上时隙开始时刻的时间，Δ为节点A与节点B的时间差。尽管节点B收到了A的数据帧，但由于节点B还未发数据，所以需等1个时隙后，在B节点时隙发出数据帧。节点B发出数据帧后，经过BA传输延时，传递到A节点，此时A节点可以计算时差，得

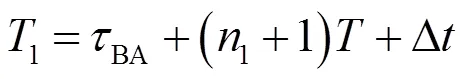
式中，为时隙持续时间。经过2个时隙，节点A再次发送数据帧，经过AB传输延时，到达节点B，此时B节点可以计算时差，得

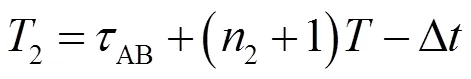
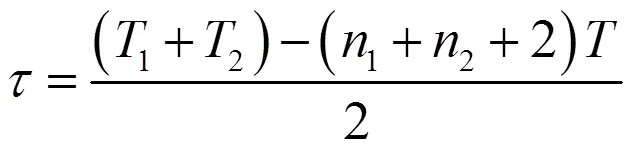
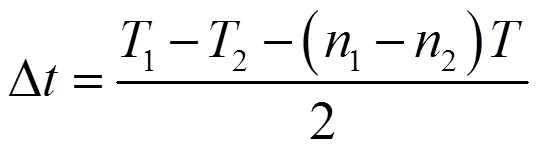
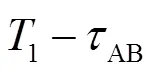
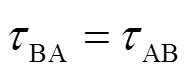
A、B节点运动时一次测量时间计算如图5所示，对节点B和节点A时间轴上①、②、③、④时间标志位发出和接收时刻进行分析。

令“①”为时刻，此时节点A与节点B相距()，如图6所示。

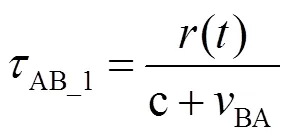
式中，表示“①”时刻路径时延。节点B在“③”时刻发出测距标志位时A、B节点相距，如图7所示。

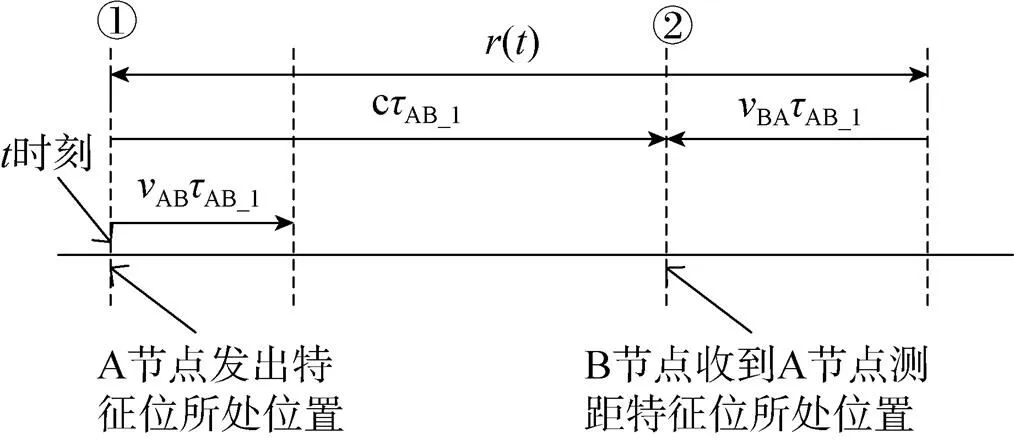
图6 “①”时刻到“②”时刻A、B节点间距离变化

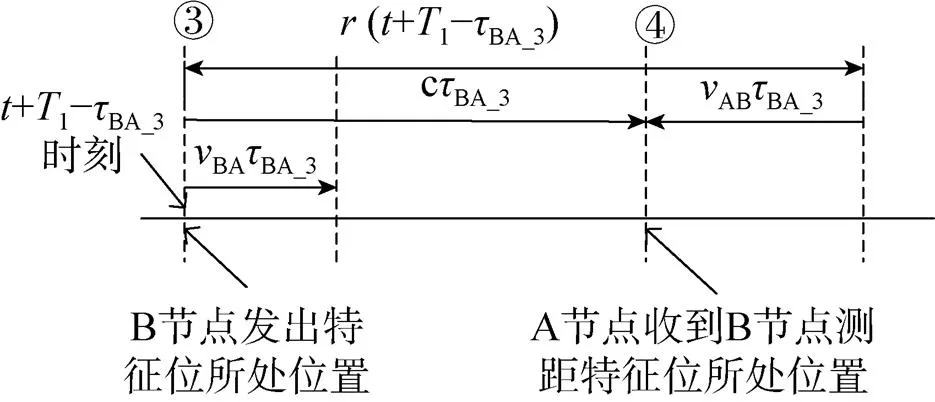
图7 “③”时刻到“④”时刻A、B节点间距离变化

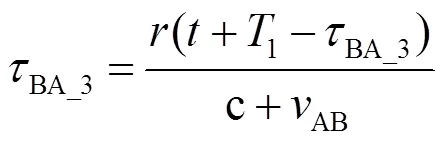
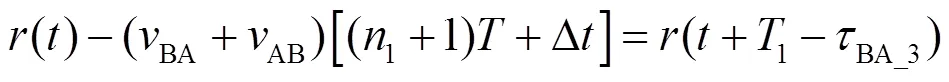
由式（2）可知

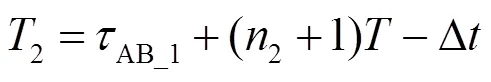
由式（1）可知

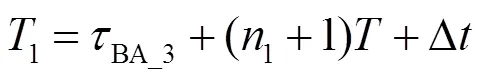
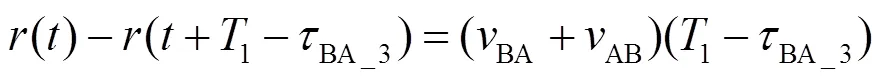
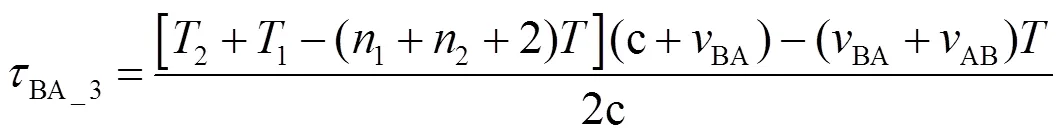
由式（9）可得

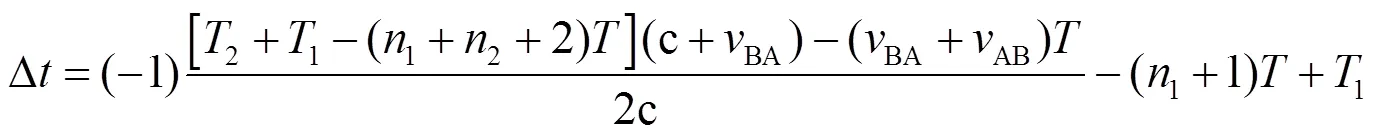
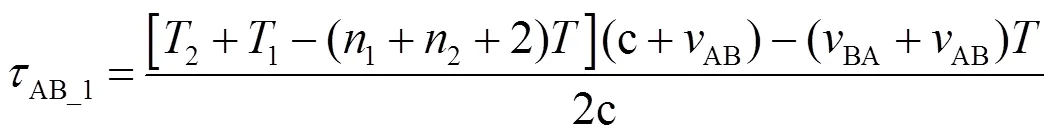
“②”时刻节点B测得时差为

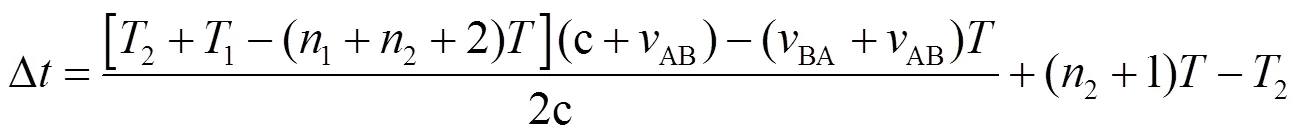
由图5、图7可知，“④”时刻节点A获得1、2，此时A、B两节点相距4，有

3 误差分析

3.1 系统零值的影响

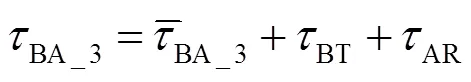
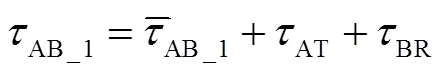
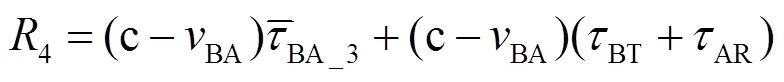
则“④”时刻A、B节点空间距离应为

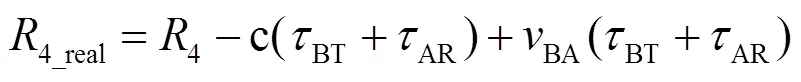
由式（8）、式（9）可得

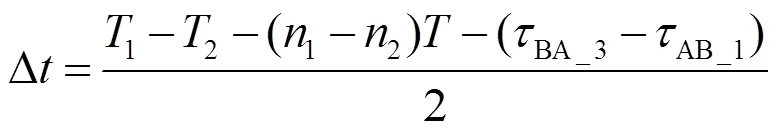
所以

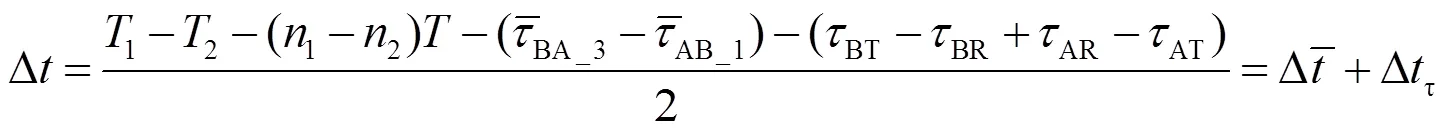
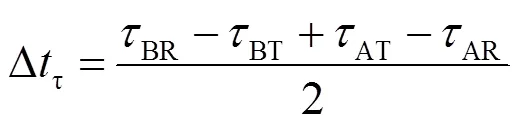
可见，如果节点收发信道设计得极其对称，则该项误差可被有效抑制。但由于元器件差异，一般情况下该项误差不可能被完全抑制，仍需通过零值标定提高时间同步精度。

3.2 速度对测距的影响

可以将式（15）分解成速度无关量4s和速度相关量4d，即

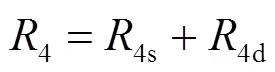
其中

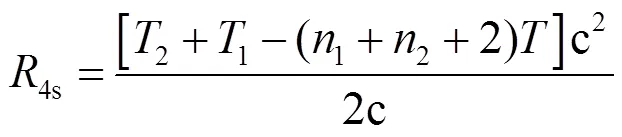
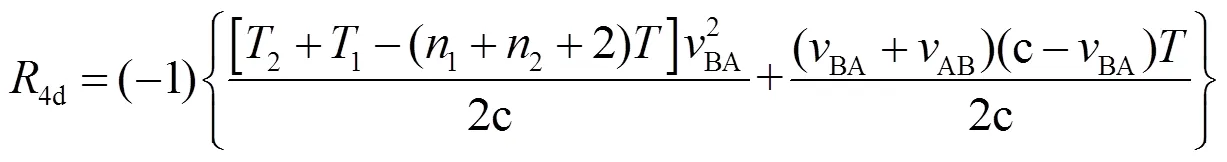
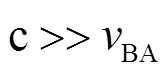
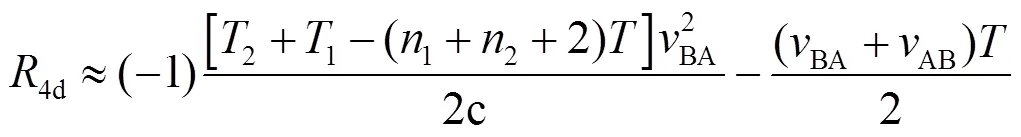
由式（8）、式（9）可将4d的第一项化简为

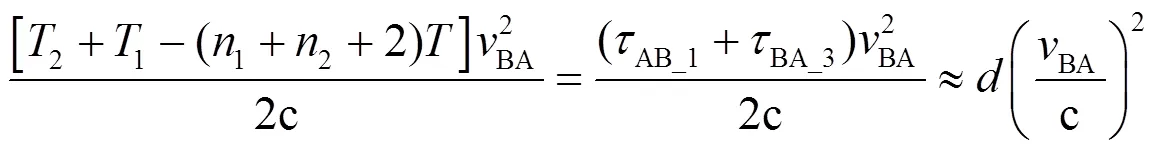
式中，为节点间距。可见，4d的第一项所产生的误差与节点间距及节点运动速度有关。设速度较快、间距较大的低轨小卫星编队飞行速度为50m/s，间距最大100km，则

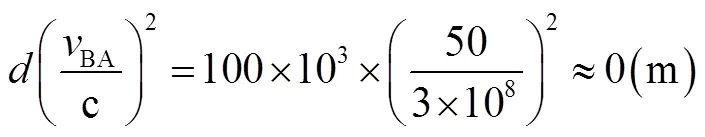
所以，此项误差可以忽略。

式（26）中的第二项误差与节点间相对速度及时隙时间有关。若相对速度与时隙时间的共同影响达到厘米级，则需通过对节点间相对速度的估计来加以修正。考虑节点间保持匀速相对运动，且相对速度对距离差没有影响，因此相对速度可以采用固定时间测距离差来求取。

3.3 系统时钟与测距周期对测距的影响

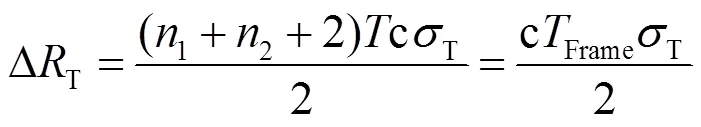
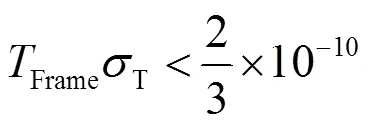
3.4 符号同步对测距的影响

编队网络采用TDMA体制，属于短时猝发通信，采用具有强相关性的前导码训练序列，利用本地前导码序列直接与接收前导码进行相关，得到具有尖锐峰值的定时度量函数。

采用数据辅助同步法测取1、2的精度取决于符号同步所采用的技术。1+2将对式（24）、式（25）产生影响，但由3.2节分析可知，式（25）中的1+2影响可以忽略不计。对于式（24），1+2对距离测量的误差表示为

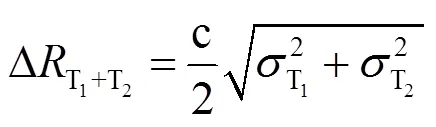
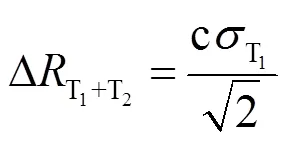
这里引用OFDM系统关于定时偏差的估计Cramer-Rao界[15]

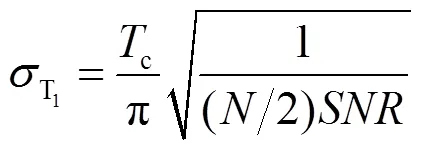
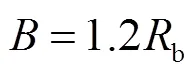
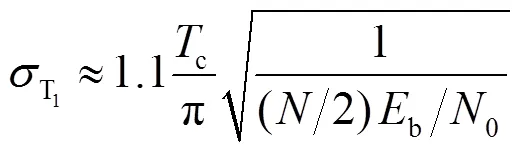
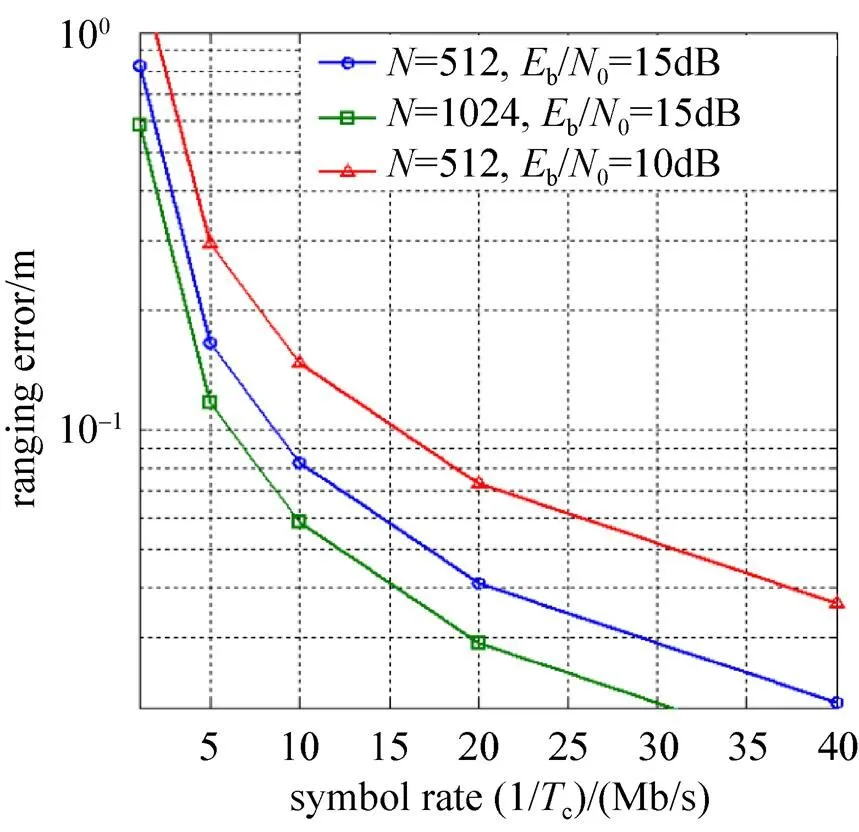
图8 N、Tc及Eb/N0的变化对测距误差的影响

3.5 天线相位中心误差[17]

在测距过程中，其观测值都是不同节点发射天线到接收天线相位中心间的距离。接收天线相位中心的瞬时位置会随输入信号的强度和方向不同发生变化，造成接收天线相位中心和天线几何中心不一致，从而导致测量误差。根据天线性能，测量误差可达数毫米至数厘米。对于高精度的测量，可以通过对观测量求差削弱其影响，也可以在设计天线时，通过试验获取天线相位中心偏差的先验信息，并利用星间相对位置补偿天线相位中心偏差引起的相对距离和时间同步测量误差。

4 网络测距与网络协议的关系

4.1 网络时间同步问题

编队网络通信中，网络时间同步非常重要，它是划分时隙实现TDMA通信的基础。网络时间同步属于自组网自同步范畴，一般在网络同步协议中进行规范。一种可能的方式是在建网过程中，由时间基准节点广播时钟信息，网络成员接收该信息完成网络时间粗同步；之后时间基准节点与每个入网节点分别完成两次应答后即可实现网络时间精同步。由式（21）可知，网络时间精同步的误差主要源自系统零值误差、系统时钟误差，以及符号同步误差。网络时间同步精度与测距精度是相关的，即测距精度达到厘米级，则网络时间同步精度为亚纳秒级。所以，为了保证数据正常接收，编队成员的间距不能低于米级。

4.2 测距精度要求对网络规划的影响

式（15）给出了飞行器编队动态测距的最终表达式，由3.2节分析可知，若TDMA时隙为0.5ms，当成员间的相对速度小于200m/s时，由速度产生的测距误差即可达到厘米级，而实际编队飞行的飞行器之间的相对速度要低得多，若在测距过程中实现测速，并按式（15）加以补偿，则速度产生的测距误差基本可以不用考虑。

这样对于飞行器编队主要的测距误差源为系统零值、系统时钟准确度、符号同步误差、天线相位中心误差，其中系统零值、天线相位中心误差为静态误差，可以通过标定予以消除，而系统时钟稳定度、符号同步误差则为随机误差，因此式（15）给出的测距值实际上是一个随机过程。

如图8所示，尽管训练序列长度、符号周期、信号的信噪比都会对测距误差产生影响，但受限于网络物理协议和接入协议对帧同步和时隙的规定，训练序列长度与符号周期在网络规划时应尽量降低对测距精度的影响，而一旦确定一般不会改变，可以按确定量来考虑。因此，对测距精度影响较大的就只有信号的信噪比和节点时钟的稳定度，前者影响节点间的通信距离，而后者影响节点时频设备的成本。

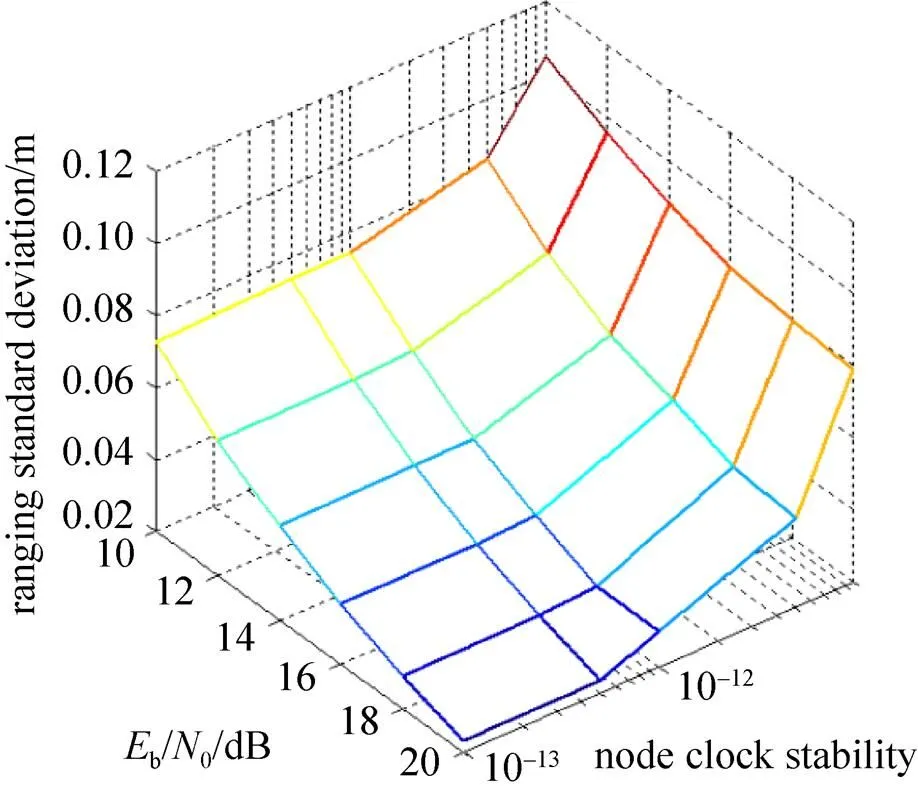
图9 节点时钟稳定度及Eb/N0的变化对测距误差的影响

图9是根据式（15）给出的一个拥有50成员编队，在时隙1ms、通信速率20Mb/s时，通信信噪比和节点时钟稳定度对测距误差的影响。可见，距离远的节点间测距误差较大，而时钟稳定度高的节点（假设编队节点具有一致的时钟稳定度）测距精度高。

5 结束语

本文针对飞行器编队网络测距需求，将微波双向测距原理扩展至网络通信。与一般测控测距原理最大的区别在于，网络通信信道是共享的，测距周期就是一个超帧时间。通过误差分析，为达到高精度（厘米级）测距，必须综合考虑通信距离与节点时钟稳定度。同时，训练序列长度与符号周期也要根据测距精度来设计。

[1] 徐劼. 小卫星编队飞行关键技术及发展趋势分析[J]. 航天电子对抗, 2007, 23(6): 24–29. XU Jie. Key techniques of small-satellite formation flight and its development[J]. Aerospace Electronic Warfare, 2007, 23(6): 24–29.

[2] 林来兴. 分布式小卫星系统的技术发展与应用前景[J]. 航天器工程, 2010, 19(1): 60–66. LIN Laixing. Technological development and application prospects of distributed small satellite system[J]. Spacecraft Engineering, 2010, 19(1): 60–66.

[3] 王炯琦, 吴翊. 编队飞行的小卫星精确定轨方法的研究[J]. 中国空间科学技术, 2005, 25(3): 8–13. WANG Jiongqi, Wu Yi. An approach for moonlet precise orbit determination based on satellite formation flying[J]. Chinese Space Science and Technology, 2005, 25(3): 8–13.

[4] 马宏, 王元钦, 陈谷仓. 编队飞行小卫星空间状态测量方法研究[J]. 飞行器测控学报, 2004, 23(2): 1–4. MA Hong, WANG Yuanqin, CHEN Gucang. Researches on the measurement of position and attitude of the formation flying small satellites[J]. Journal of Spacecraft TT&C Technology, 2004, 23(2): 1–4.

[5] 秦勇, 惠蕾放, 刘晓旭, 等. 分布式空间系统星间通信组网技术研究综述[J]. 空间电子技术, 2015(4): 1–10. QIN Yong, HUI Leifang, LIU Xiaoxu, et al. Survey: inter-satellite networking technologies of distributed space systems[J]. Space Electronic Technology, 2015(4): 1–10.

[6] 史凤振. 小卫星编队组网机制研究[D]. 西安：西安电子科技大学, 2014. SHI Fengzhen. The research of networking mechanisms for micro-satellites formation[D]. Xi’an: Xidian University, 2014.

[7] 王建宏, 许莺, 熊朝华. 无人机编队飞行的自适应控制设计[J]. 华东交通大学学报, 2016, 33(1): 1–8. WANG Jianhong, XU Ying, XIONG Zhaohua. Adaptive control design in UAV formation flight[J]. Journal of East China Jiaotong University, 2016, 33(1): 1–8.

[8] GUPTA LAV, JAIN RAJ, VASZKUN GABOR. Survey of important issues in UAV communication networks[J]. IEEE Communications Surveys & Tutorials, 2016, 18(2): 1123–1152.

[9] MARCONATO E A, MAXA J A, PIGATTO D F, et al. IEEE 802. 11n vs. IEEE 802. 15. 4: a study on communication QoS to provide safe FANETs[C]//46th Annual IEEE/IFIP International Conference on Dependable Systems and Networks Workshops, 2016: 184–191.

[10] SCHIAVONE L J. Airborne networking approaches and challenges[C]//IEEE Military Communications Conference, 2004: 404–408.

[11] KULLA E, SAKAMOTO S, IKEDA M, et al. MANET approaches for airborne networks: a survey[C]//16th International Conference on Network-based Information Systems, 2013: 66–70.

[12] 黄波, 胡修林. 北斗2导航卫星星间测距与时间同步技术[J]. 宇航学报, 2011, 32(6): 1271–1275. HUANG Bo, HU Xiulin. Inter-satellite ranging and time synchronization technique for BD2[J]. Journal of Astronautics, 2011, 32(6): 1271–1275.

[13] 范丽, 张育林, 曾国强. 小卫星星座及其自主运行技术[J]. 上海航天, 2002(4): 29–32. FAN Li, ZHANG Yulin, ZENG Guoqiang. The autonomous technology of constellation[J]. Aerospace Shanghai, 2002(4): 29–32.

[14] 梁瑾, 宋栋梁, 李嘉. 某小型无人机编队控制器设计及试飞验证[J]. 飞行力学, 2016, 34(4): 73–76. LIANG Jin, SONG Dongliang, LI Jia. Design and flight test for formation control laws based on small UAVs[J]. Flight Dynamics, 2016, 34(4): 73–76.

[15] MOOSE P H. A technique for orthogonal frequency division multiplexing frequency offset correction[J]. IEEE Trans. on Communications, 1994, 42(10): 2908–2914.

[16] 王立冬, 胡卫东, 郁文贤. 时延－多普勒频移对伪码捕获影响的性能分析[J]. 系统工程与电子技术, 2001, 23(6): 79–81,86. WANG Lidong, HU Weidong, YU Wenxian. Performance analysis of delay-doppler effect in acquisition of PN code[J]. Systems Engineering and Electronics, 2001, 23(6): 79–81,86.

[17] 马宏, 王元钦, 陈谷仓. 编队小卫星间相对测距和时间同步方法研究[J]. 装备指挥技术学院学报, 2006, 17(2): 67–71. MA Hong, WANG Yuanqin, CHEN Gucang. Research on relative ranging and time synchronization between formation flying small satellites[J]. Journal of the Academy of Equipment Command & Technology, 2006, 17(2): 67–71.

Research on ranging technique for spacecraft formation flying network

WANG Pengyu

（The 27th Research Institute of China Electronics Technology Group Corporation, Zhengzhou 450047,China）

For the ranging problem in spacecraft formation flying network under autonomous TT&C, a high accuracy ranging method in TDMA communication is presented. The nodes in network can implement ranging process with each other without interrupting their communication. The accuracy of the ranging method can reach centimeter level. The principle of the ranging method is discussed in detail and the error sources are analyzed.

Spacecraft formation flying; Network; Inter-satellite ranging

V217

A

CN11-1780(2019)02-0022-09

2018-10-21

2018-12-11

王鹏宇 1976年生，博士，高级工程师，主要研究方向为卫星通信与飞行器测控系统总体设计。