基于绝对式准静态校准的测力传感器分析

陈 静，孔德仁，郭 彬，张喜英，顾廷炜，陈金刚

(1.北京交通大学海滨学院电子与电气工程学院，河北黄骅 061100；2.南京理工大学机械工程学院，江苏南京 210094；3.黄骅市住房和城乡建设局，河北黄骅 061100)

0 引言

压电式压力测量系统具有固有频率高、动态特性好等优点，因而被广泛地应用于动态压力测试领域。然而，由于系统低频特性不够理想，若采用静态标定的方法对其进行校准时不可避免地会产生电荷泄漏和系统响应漂移等问题，导致获得的传感器灵敏度参数准确度不高，且静态标定加载时间过长会严重影响传感器的使用寿命；若采用激波管等动态标定的方法，由于阶跃压力的平台持续时间较短，因而无法对系统的低频特性进行校准，此外，激波管产生的压力幅值较低，无法实现高压传感器的动态校准[1]。因此，为了提高压电式压力测量系统的校准精度，可采用落锤液压动标装置对其进行准静态校准。该方法主要分为比对式和绝对式，前者采用的标准压力监测系统常选用多路价格昂贵的高精度压电式压力测量系统构成，虽然有着较高的校准精度，但试验成本很高，因而采用高精度的测力传感器来监测压力[2]。

对于力监测压力的绝对式准静态校准方法，若采用螺栓连接的方式将力传感器固定在两个过渡件上，螺栓预紧力在一定程度上影响其测量精度，此外，由于锤头撞击活塞杆的过程中必然会受到惯性力的影响，导致测得的力与校准原理中活塞作用力F是有差异的，与此同时，试验过程中由于重锤组件与导向系统之间存在间隙，使得重锤打击中心与精密活塞杆中心不一致，导致偏心力矩的存在，而精密活塞杆与活塞缸之间的摩擦力是和摩擦系数及弯矩产生的正压力成正比的，因此该摩擦力不可控[3]。基于以上分析，根据此安装结构按常规方法得到的力和压力的关系模型与真实情况不符，为了精确测量锤头撞击精密活塞杆时力的大小，需研制测力传感器，该传感器具备良好的动态特性和较高的精度，且结构上能适用于现有的落锤装置，具体设计要求如下：

(1)锤头便于安装并能保证安装后打击活塞不偏心；

(2)所测得的力量程应满足压电式压力电测系统的校准需求，准静态压力校准范围为 0～1 000 MPa，活塞杆以1 cm2面积作为指标考核值，则要求所设计的测力传感器量程包含 0～100 kN；

(3)固有频率至少应高于压力脉冲信号有效频带的3～5倍以减小动态误差；

(4)结构简单，易于加工并具有较好的抗弯能力。

1 测力传感器的结构

根据落锤装置的结构特点及测力传感器的设计要求，拟将测力传感器设计为与锤头一体，即将锤头作为弹性敏感元件，从而可不借助过渡件直接将传感器安装在现有锤体上，如图1所示。

图1 传感器内部尺寸结构图

传感器的敏感元件选用柱形结构形式，中间位置粘贴有多个应变片用来测量力的大小。粘贴方式如图2所示，选用同一批号且阻值均为120 Ω的应变片粘贴在锤头圆柱部分的中间位置。为了尽可能消除锤头打击活塞偏心产生弯矩的影响，传感器的电桥电路实现如图3所示[4]。该电桥电路可以提高传感器的输出灵敏度，其中工作应变片在电路中用对臂的方式，而补偿应变片与工作应变片采用邻臂的方式接入电桥中，此种连接方法不但起到了温度补偿作用，还具有抵抗打击偏心产生的弯矩的能力。根据所选的锤头材料，结合应变片所测得的应变关系得到应力大小[5]。

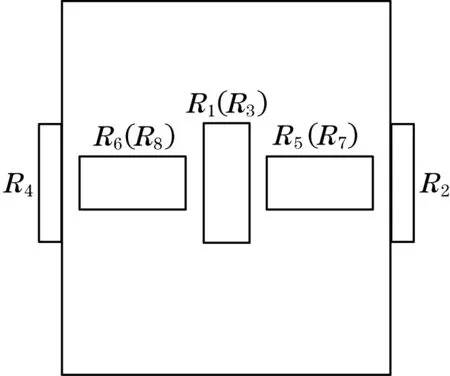
图2 应变片粘贴图

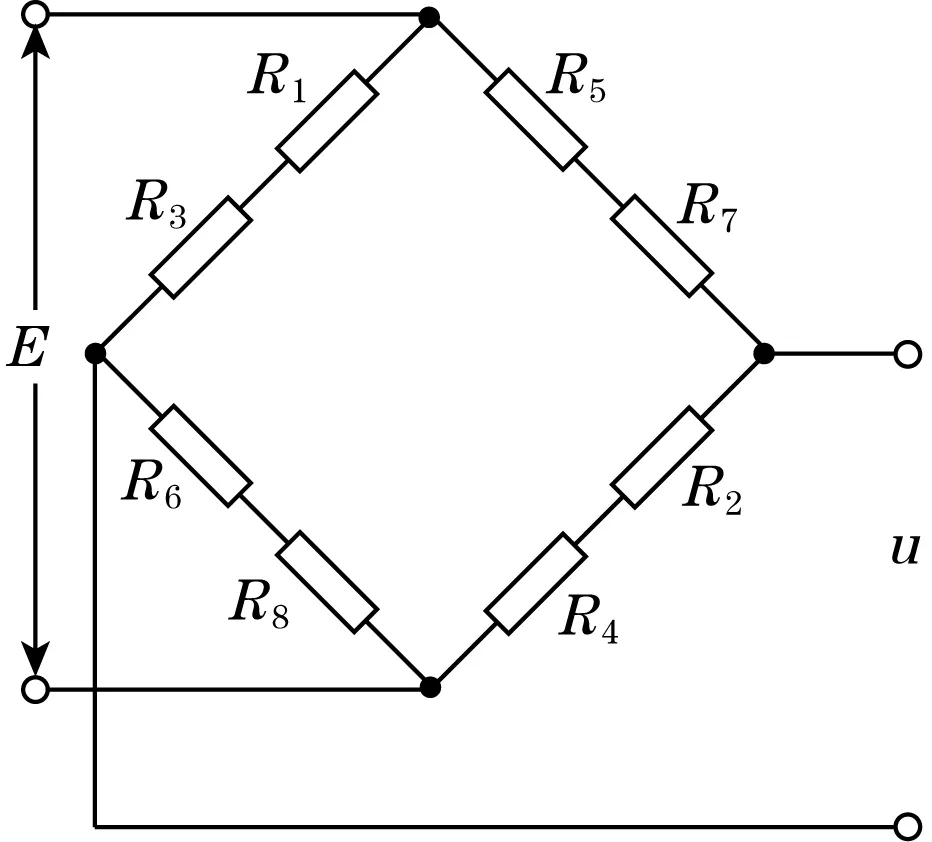
图3 电桥电路连接图

测力传感器的整体结构及实物图如图4所示，其中底部加球头设计以减小锤头与活塞杆的接触面积，从而减小撞击过程中对锤头和活塞杆的磨损；上端加入轴向定位结构以保证重锤垂直打击活塞杆，减小偏心力矩；设计专用的保护罩对其进行防护，以免在试验过程中对应变片造成损伤导致测量结果有偏差。

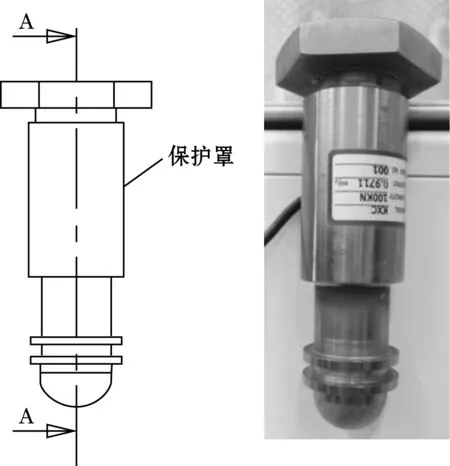
图4 传感器整体结构及实物图

2 测力传感器的理论计算

材料选用35CrMnSiA低合金超高强度钢[6]，该材料强度较高，综合机械性能较好，是应变片式传感器尤其是大吨位传感器弹性体的理想材料，其理论分析计算如表1所示。由表中数据可知：

(1)在测试范围内敏感元件的轴向应力σ<[σ]=1.275×109Pa，符合强度要求；轴向应变ε<1 000 με能保证较好的线性及迟滞特性；

(2)造压油缸内的压力信号波形呈半正弦型，若定义压力信号的归一化频谱密度由1下降至其 2%处的频带作为有效带宽，则对于脉宽为3～12 ms的理想半正弦信号而言，其有效频带范围为113～454 Hz[7]。根据以上分析可知，研制的专用测力传感器的固有频率远高于被测压力信号的有效频带，即测量系统的工作频带能够包容被测信号的有效频带，测量时的动态失真可以忽略不计，自研力传感器的动态特性满足准静态校准的要求。

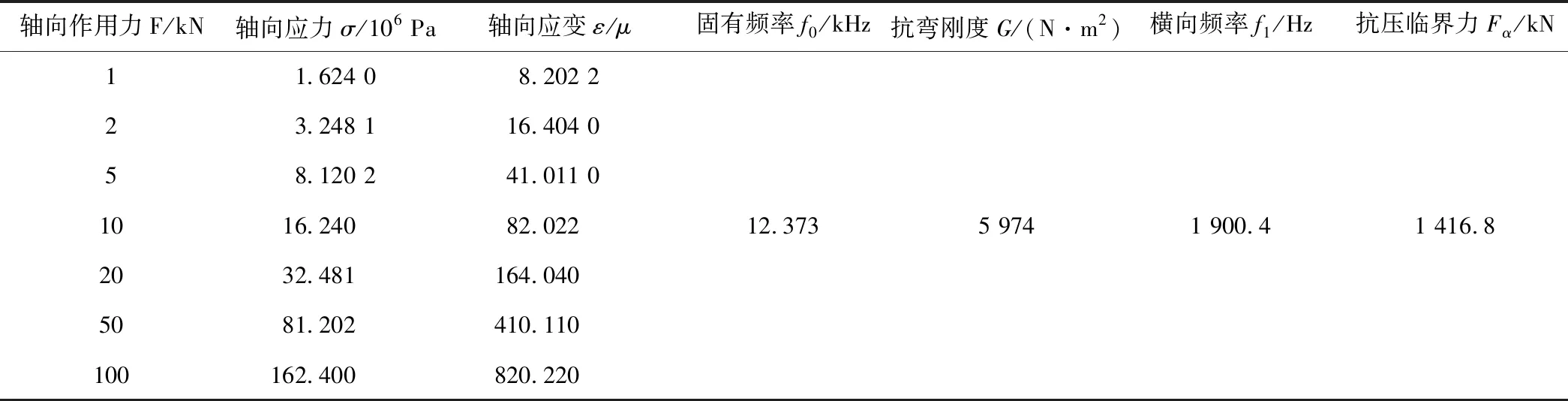
表1 传感器弹性元件理论计算结果

(3)抗压临界力远大于测力传感器量程范围内的最大值，说明测力传感器具有较好的抗弯能力。

通过对测力传感器弹性元件进行理论计算可知，该传感器设计合理。

3 测力传感器的仿真分析

为了进一步验证力传感器的应力、应变均在合理范围之内，采用 workbench14.5对传感器进行了仿真分析。按照力传感器的设计尺寸建立仿真模型，并选用Johnson-Cook模型作为35CrMnSiA材料的强度模型[8]。在测力传感器的中间位置选取一特征点，由表 2中仿真结果可知，测力传感器的敏感元件在测试范围内的轴向应力小于其屈服应力，该传感器满足强度要求；由图5所示传测力传感器的模态分析结果可以发现传感器产生横向振型时对应的固有频率为f1=1 890.5 Hz ，在竖直方向振动的固有频率为f6=12 693 Hz ，由此可知，测力传感器的固有频率远高于被测压力信号的有效频带，测量时的动态失真可以忽略不计，该测力传感器的性能满足设计要求[9]。

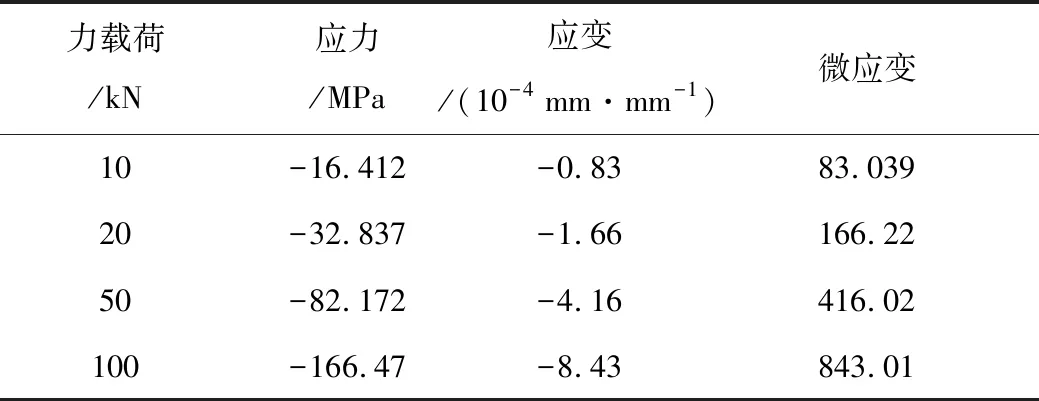
表2 传感器仿真结果( 6 ms)

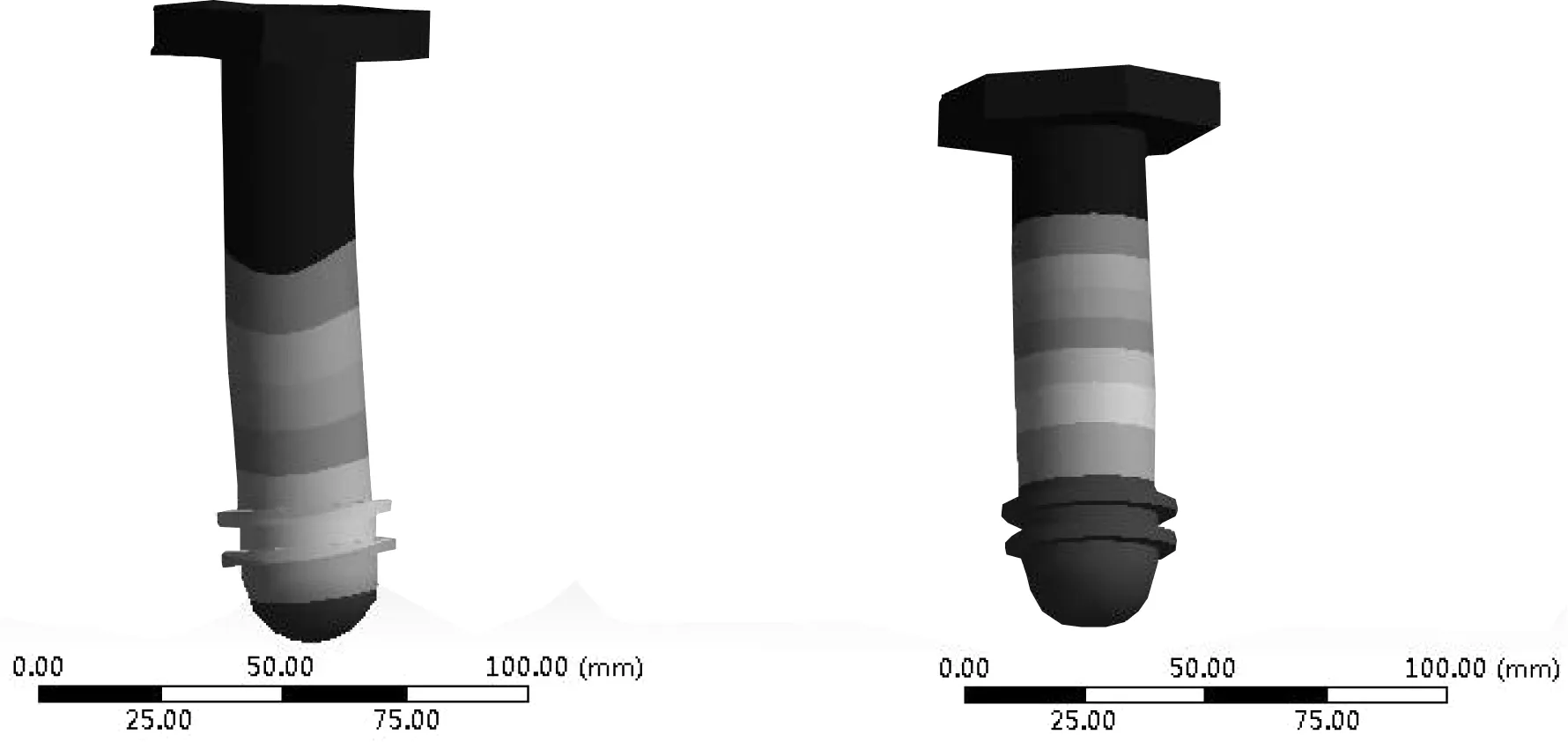
图5 传感器模态分析结果

4 测力传感器静动态特性试验

对测力传感器进行静态标定[10]，结果如表3所示，所设计的测力传感器静态特性良好，满足试验要求。

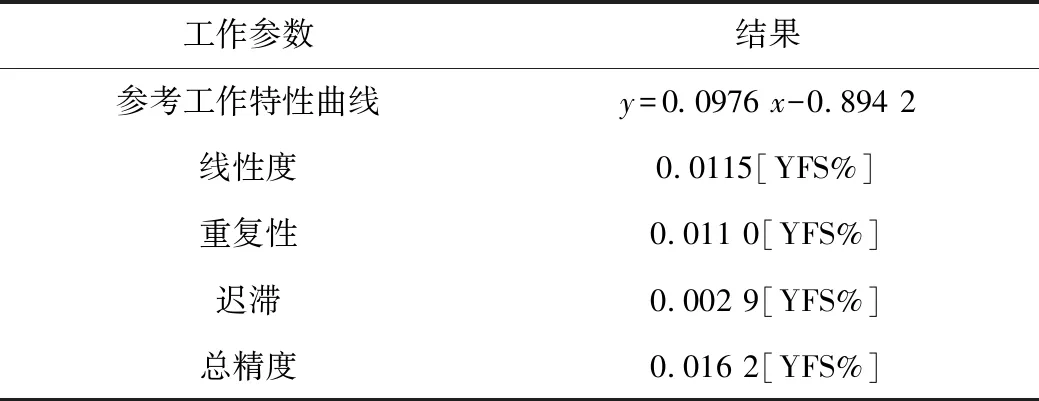
表3 传感器静态特性指标

注：x为输入力值，N；y为系统输出值，放大倍数：10 000，mV

测力传感器动态校准试验方案如下：将测力传感器竖直放置在脆性材料上，脆性材料由置于底座的两支撑块支承，并施加力直至其断裂，如图6所示，在断裂瞬间测力传感器的输入信号为负阶跃力，通过对已知的输入信号和传感器的输出信号进行 FFT运算获得其幅频特性曲线[11]。

试验时，通过千斤顶向高速钢施加力直至其断裂，因此在高速钢断裂前测力传感器的输出信号呈阶梯状，断裂瞬间为负阶跃信号。如图7分别为系统响应原始信号(采样频率100 kHz，采样时间5 s)及截取原始信号中有效信号并将其转换成正阶跃信号后进行归一化处理得到的曲线。

(a)阶跃力发生器

(b)动态校准系统图6 阶跃力发生器及传感器动态校准系统

(a)系统响应原始信号

(b)截取有效信号并进行归一化处理图7 力值测量系统阶跃响应曲线

对力值测量系统的阶跃响应信号进行 FFT运算获得图8所示幅频特性曲线，其在 0～1 kHz范围内为一条较平坦的直线，则有效频带上限为1 kHz；在1～2 kHz范围内有一共振峰，其产生的原因是由于阶跃力发生器在力传递过程中不能很好地与传感器轴线平行，导致所加载荷与传感器的轴线有一定的夹角，从而激发了测力传感器的横向振动频率；在12～13 kHz范围内有一主共振峰，其对应的频率即为测力传感器的固有频率。根据以上分析可知，测力传感器的动态特性试验结果与上文中的理论计算和仿真分析结果相吻合，因此传感器的固有频率远高于被测信号的有效频带，其动态特性满足准静态校准的要求。

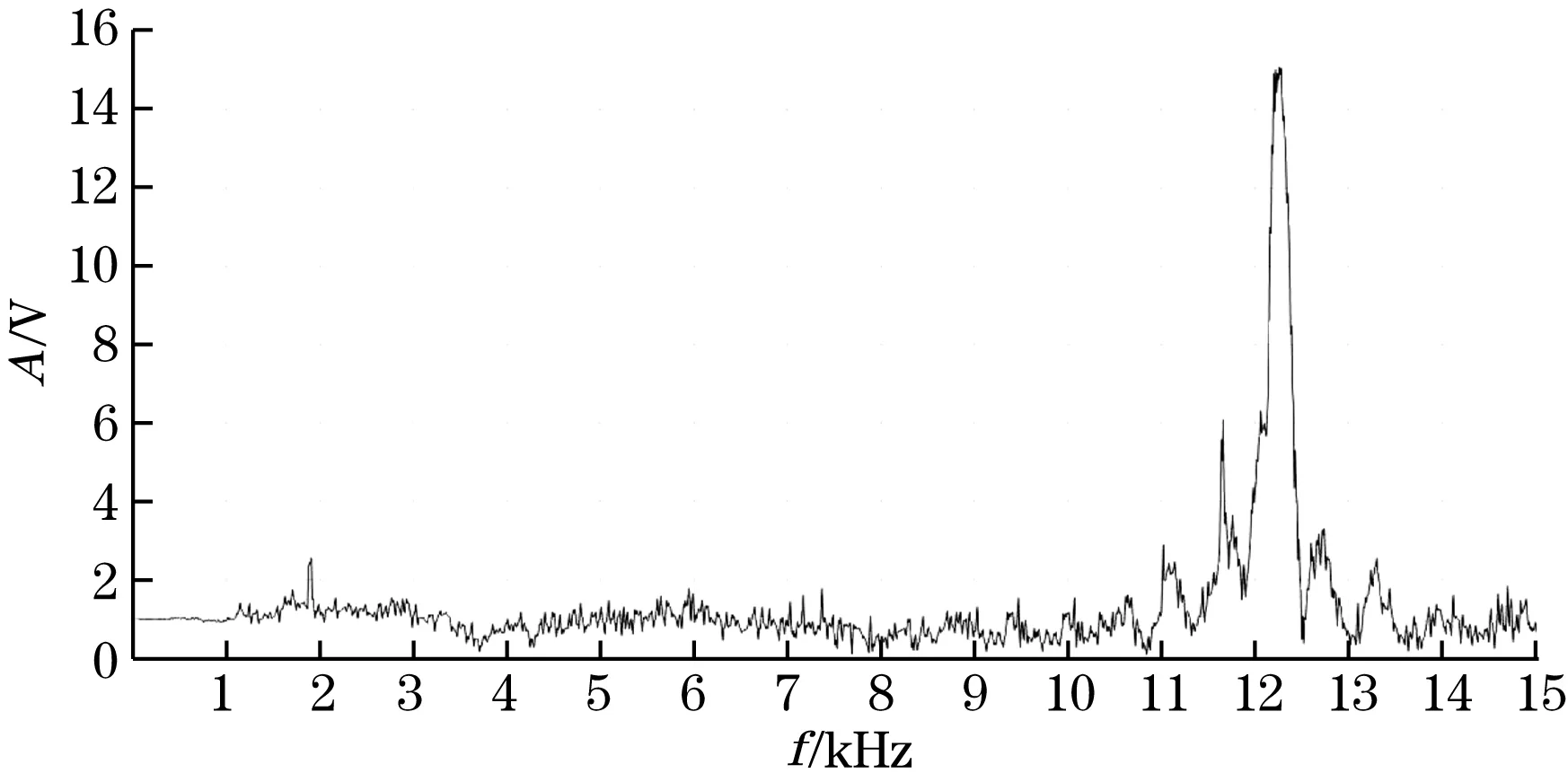
图8 测力系统幅频特性曲线图

5 结束语

由理论计算、仿真分析及试验验证可知，采用该方案设计的测力传感器可用于压力传感器绝对校准中，并且可有效消除预紧力和惯性力对实验结果的影响。