基于互相关算法的挡板式内循环流化床参数测量
王中武,李 俊
(南京工业大学,江苏南京 211816)
0 引言
气固两相流是两相流体系中常见的流动形式,针对其的测量已广泛存在于工业领域。内循环流化床(internally circulating fluidized bed,ICFB)是一种使气固两相流达到流化状态的设备,其具有高度低、结构简单、反应过程辨识度高、负载控制范围大、气固反应效率高等优点[1-2]。但由于ICFB内流体流动过程中具有非均匀性和不对称性的特点且随机多变[3-4],目前依然无法实现针对ICFB内部流体参数的准确测量,所以研究内循环流化床内气固两相流的参数测量方法具有重要意义。
电容层析成像(electrical capacitance tomography,ECT)是一种多相流参数检测技术,具有响应速度快、干扰小、成本低、安全性能好等优点[5-6],近年来,在工业检测领域中得到了广泛的应用。M. Sun等[7]利用双截面ECT系统和互相关算法检测了气力输送装置中煤粉灰流速;Y. T. Makkai等[8]通过ECT测量数据并利用数值模拟估算气固两相流的颗粒数度、颗粒间接触力等参数。这些研究都为ECT技术检测内循环流化床提供了试验基础。
本文针对挡板式内循环流化床中气固两相流的流动参数检测设计了一套三电极的ECT系统,采用交流激励,将电容值的多通道检测应用到颗粒流动参数检测中,结合互相关算法,实现了对气固两相流流动过程中的流速、浓度、质量流量等参数的测量。
1 挡板式流化床检测系统
图1(a)给出了设计好的挡板式流化床的内部结构图。为了准确地测得床内参气固两相流运动参数,结合挡板式流化床的结构特性,本文将床体底部的布风板又当作激励电极使用,另外两块检测电极分别位于中间挡板底部的左右两端,间距为固定值。
图1(b)给出了测速系统的框架图,测速系统的工作原理:上、下游测速电极与激励电极(布风板)之间的电容值分别通过C/V转换电路转化为电压值;C/V转换电路出来的信号,经过正/反放大电路以后通过ADG436,如图2所示,输入信号A和输入信号B是两路完全相同的信号,只是在相位上相差了180°;ADG436的IN1管脚输入的控制信号是由输入信号A或B通过电压比较器而产生的方波信号,控制信号的频率和正弦信号A/B的频率是完全相同的,所以D1管脚输出的为正弦信号的上半部分;最后通过二阶低通滤波电路传输到模数转换器,再由其传输给主控芯片进行数据的处理和分配。
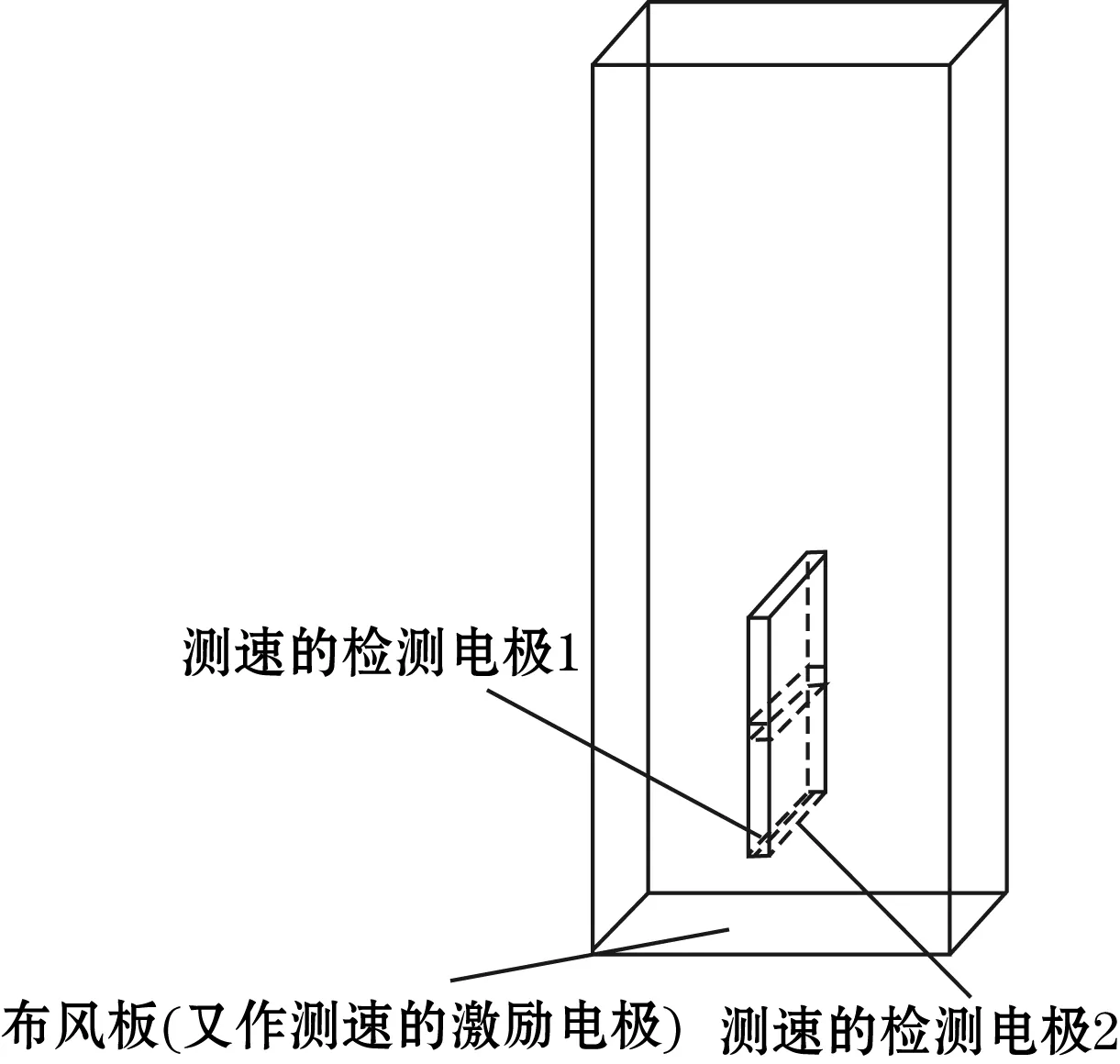
(a)挡板式流化床内部结构图
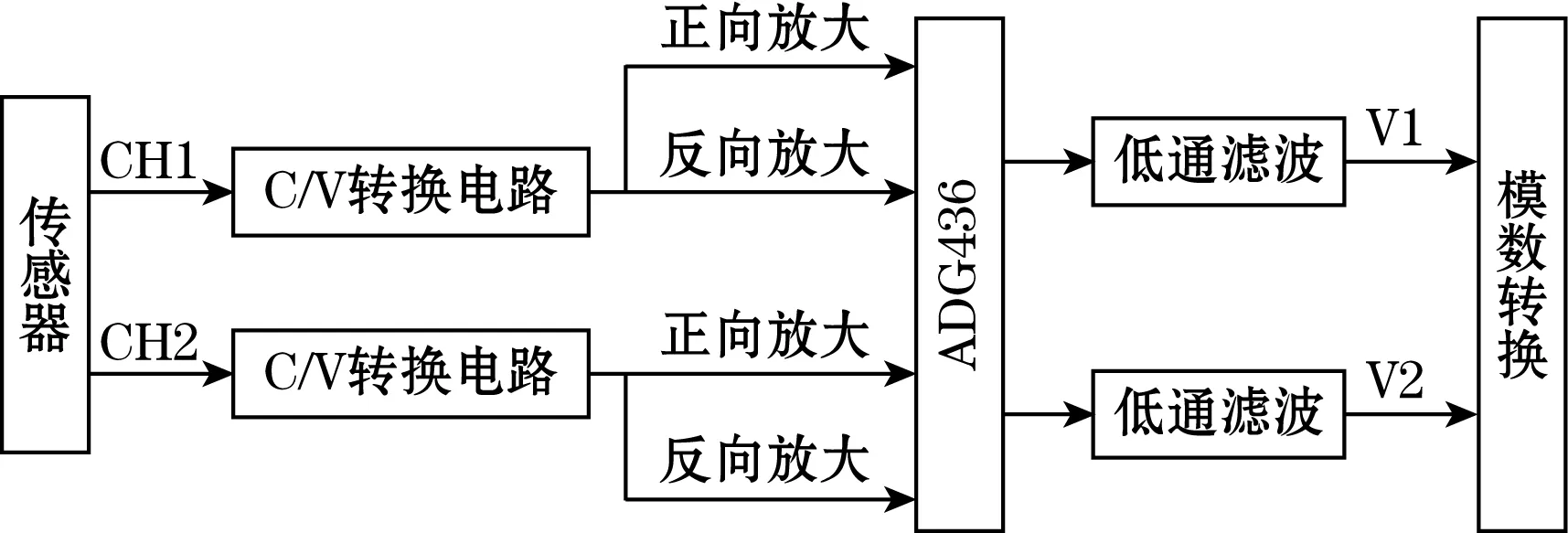
(b)测速系统的框架图图1 挡板式流化床检测系统
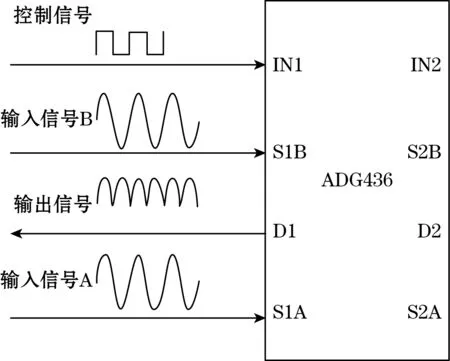
图2 测速信号原理图
2 流化床中相关参数测量的理论基础
2.1 流速的测量原理
本文设计的ECT系统同时检测上、下游电极的电容值,当固相介质流过上、下游电极时,其在时间上会有一个滞后性,从而可以将流速的计算转化为渡越时间的计算[8]。图3给出了互相关测速系统的结构框图。本系统中由于传感器的尺寸大小已固定,所以上下游之间的距离L是已知值。
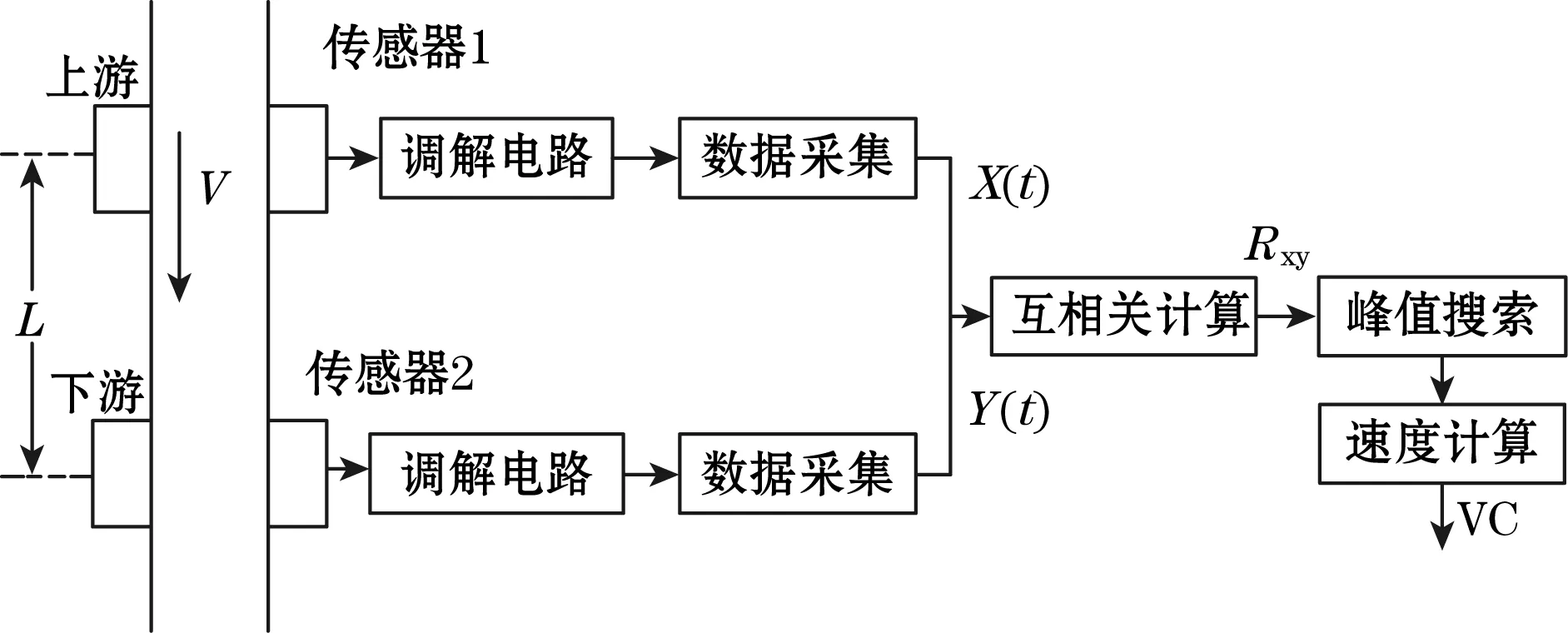
图3 互相关测速系统原理图
图3中x(t)表示上游传感器输出的信号,y(t)表示下游传感器输出的信号,x(t)和y(t)极为相似,它们只是在时间上有一个 的延时,又称2个信号的渡越时间,所以表示为
x(t)=y(t+τ0)
(1)
2个信号x(t)和y(t)的互相关函数Rxy为
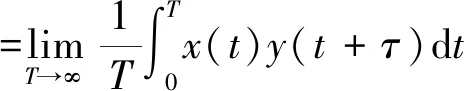
(2)
将式(1)代入式(2)中化简得:

(3)
由自相关函数的特性[9]可以知道,当τ=τ0时,Rxy能够取到最大值,所以要求介质的流速就必须求Rxy函数峰值对应的τ值。
2.2 相浓度的测量原理
固相介质和气相介质在流化床中具有不同的介电常数,所以当两相流通过上下游检测区域时,由于浓度分布的不同,对应的电容值也将发生变化[10]。所以可以用电容值的大小来衡量流化床中固相介质的浓度。如式4所示:
(4)
式中:βsolid为固相浓度;Vsolid为固相体积;V为气相和固相的总体积;εeff为气固混合的等效介电常数;εgas为固相介电常数,εgas为空气介电常数。
2.3 质量流量的测量原理
固相介质在流化床中运动时瞬时的质量流量M(t)可以用式(5)表示:
M(t)=k·S·ρ·veq·βsolid
(5)
式中:k为常数;S为固相流过的截面积;ρ为固相介质的密度;veq为流体的运动速度。
对于已设计好的传感器和介质,S和ρ都是已知量,所以式(5)又可以表示为
M(t)=K·veq·βsolid
(6)
K值可以通过实验标定测得,所以可以用veq和βsolid的乘积来衡量质量的大小。
3 内循环流化床实验的分析
实验以平均粒径为1 mm的石英玻璃圆珠为检测对象,所通气体为事先经空压机存储到储气罐的室内空气。气体从储气罐出来经三通阀流入两个分别接有流量计和压力表的管道,通过改变管道气体流速实现流化。数据采集系统将采集到的离散数据送到上位机处理,如图4所示。

图4 实验装置
3.1 上下游区域一致性实验
根据互相关算法的测量原理,当介质流过上、下游电极的检测区域时,会产生两路相关系性很强的电容信号,需要获取采集信号中最相似的两个点[11]。所以这两个点在对颗粒流速的计算中起到决定性作用,这两路信号的相关性就直接影响流速测量的准确性。所以实验需要验证系统两路信号的一致性,采样率设置为10 kHz。
向流化床内加入2 000 mL的玻璃颗粒,对左侧气室通入流量为10 m3/h、右侧气体流量为20 m3/h时,采集颗粒流过传感器2个电极的电压值,如图5所示。由图5可知,上、下游的电容噪声信号极为相似,且曲线在时间上存在一定的延时,另一方面也反映出传感器的合理性以及系统具有较高灵敏度。
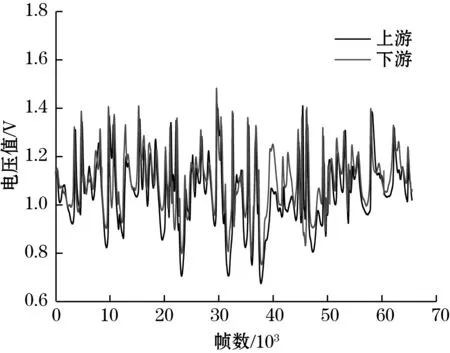
图5 上/下游电压值
3.2 相浓度的数据分析
已测得满管状态下的电压值1.389 V,空管状态下的电压值为0.254 V。给定传感器入口气体流速为uf=1.254 m/s、um=0.44 m/s,图6给出了实际采集的电压值。所以由式(4)可以算得介质浓度的相对分布,如图7所示。由图7可知,浓度的分布随着介质在两气室中的循环流动且不断变化。由图6可知,测得的电压值变小,是由于流化床床底产生的气泡导致的,气泡越大测得电容值越小,浓度也越小。对比图6和和图7可知,曲线的走势基本相同,由此可以用归一化的电压值衡量介质在流化床中的浓度。
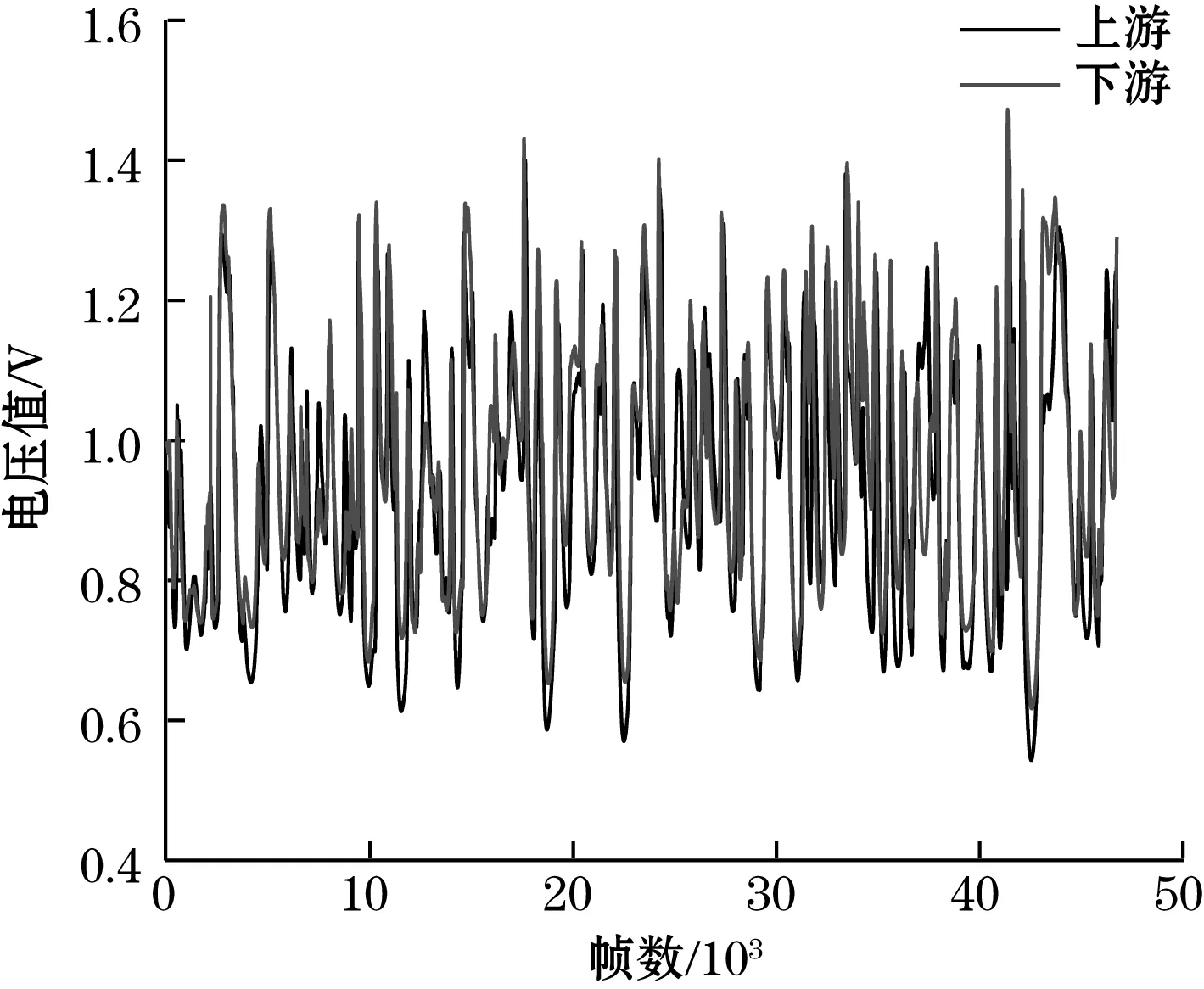
图6 uf=1.24 m/s、um=0.44 m/s时的上/下游电压
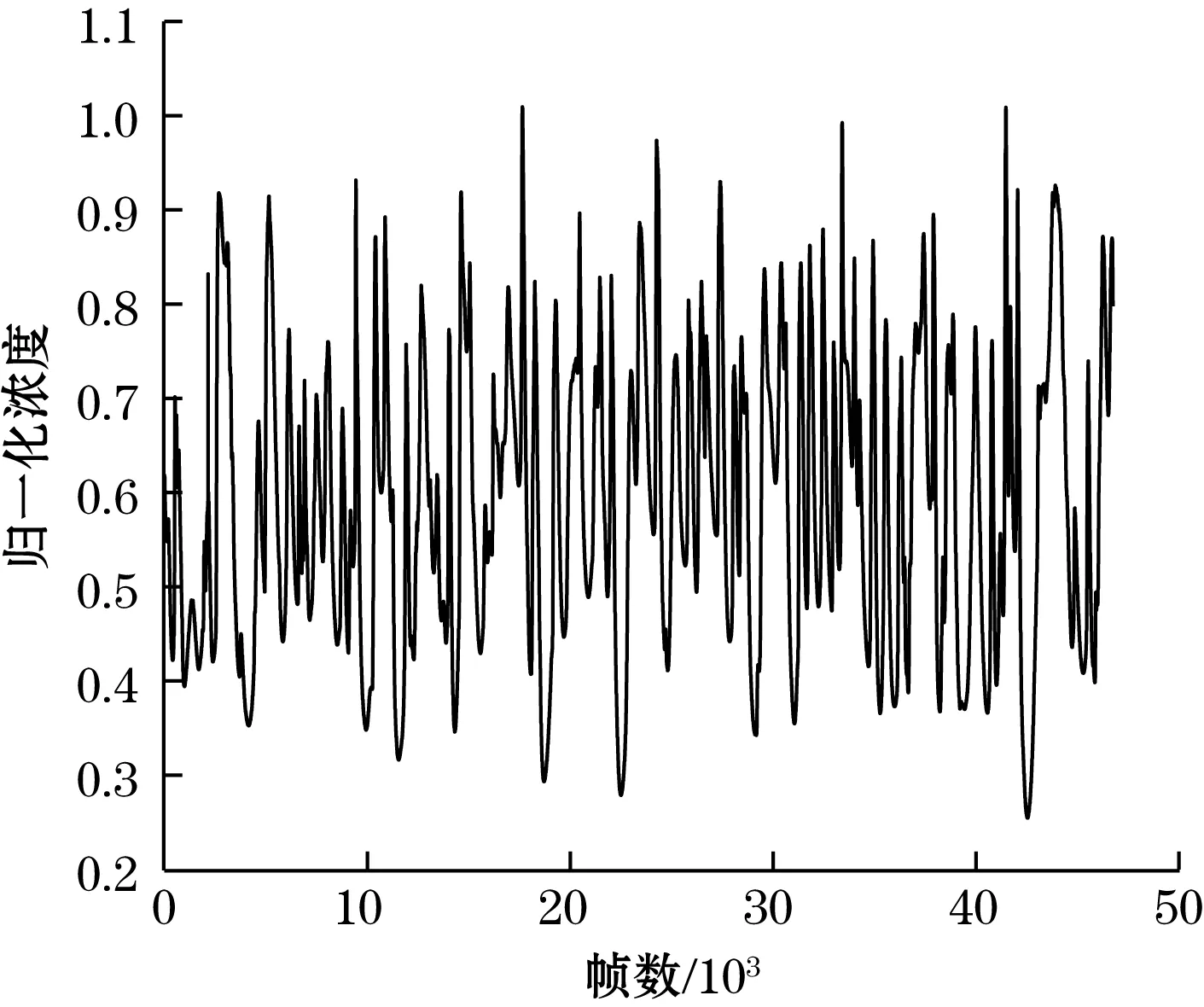
图7 uf=1.24 m/s、um=0.44 m/s时的相对浓度
3.3 流速的数据分析
3.3.1 第1组工况(uf=0.89 m/s、um=0.44 m/s )
根据之前的实验,气流流量小于9 m3/h时不能起到流化的效果。所以给定右侧气室气流流量为10 m3/h(气流流速为0.44 m/s),左侧为20 m3/h(气流流速为0.89 m/s)。由于内循环流化床结构的不规则性,所以其运动速度也比较复杂,在这种情况下抽样了102 400个数据进行分析,由互相关算法,可以计算出该工况下的颗粒的流速。选择的采样频率为10 kHz,上、下游电极间的距离L=6 mm,N=1 024,当N=1 024时将数据分成了100组,运用相关算法在MATLAB中可以计算出流体的速度,从100组中随机抽取了一组数据。图8(a)为1 024个上下游数据绘制的曲线,图8(b)是运用相关算法计算得出的相关性曲线。由图8可以看出,相关性最大时对应的延时帧数为150帧,所以τ=0.015 s,v=0.4 m/s。
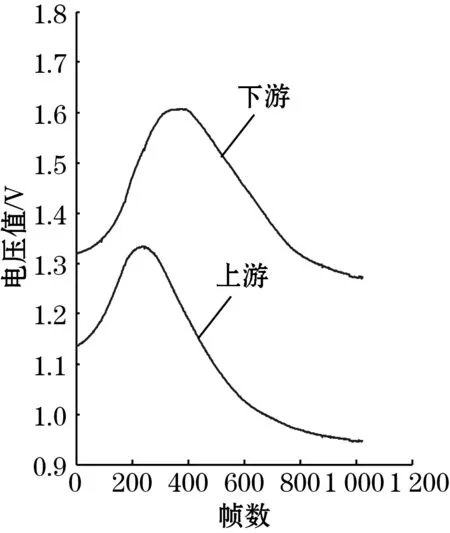
(a)上下游数据图
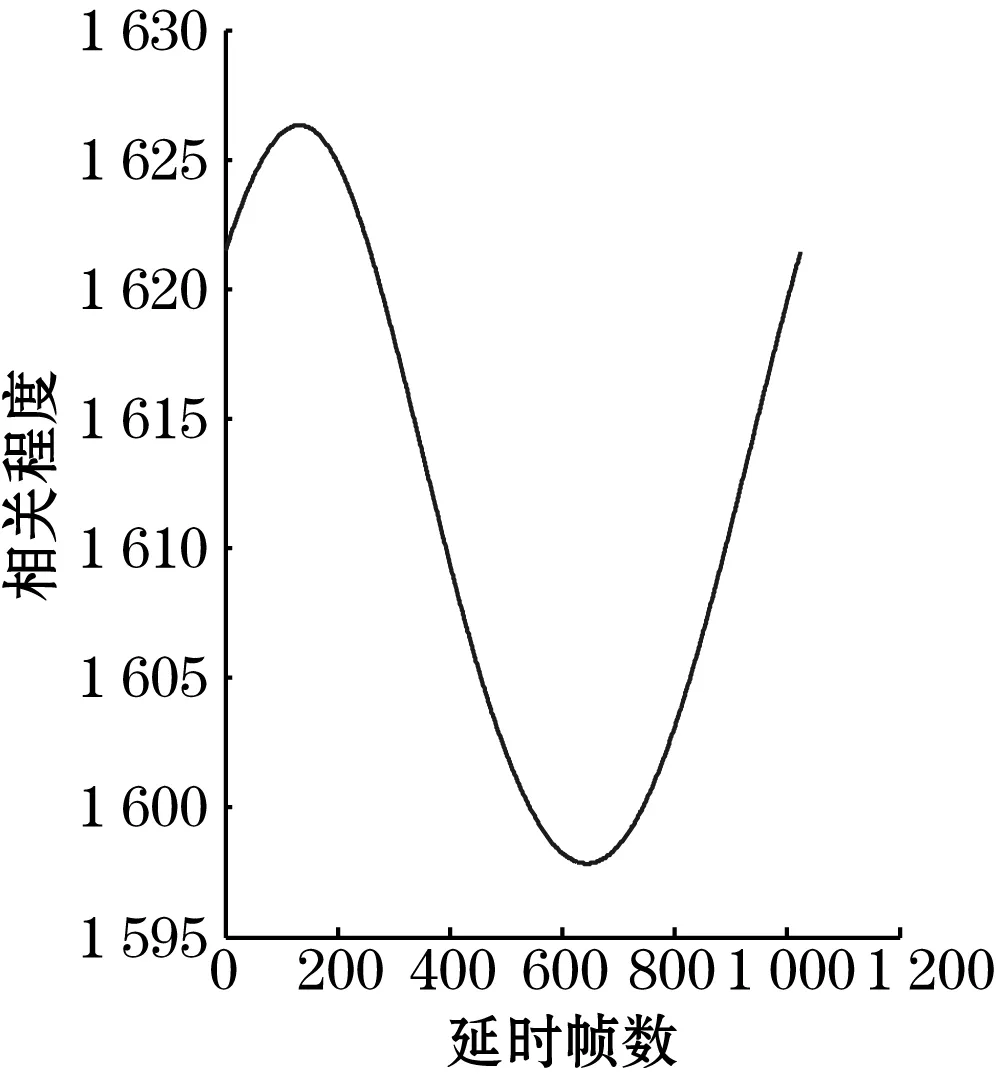
(b)相关曲线
图9给出了100组数据的流体速度,由图9可以看出:颗粒在挡板式内循环流化床中运动的速度是不规则的;介质流动过程中某一时间内颗粒速度是保持恒定的;在这种工况下颗粒的速度基本都小于0.5 m/s。
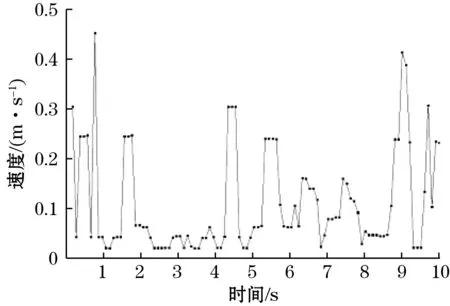
图9 第1组工况下流速—时间变化曲线
3.3.2 第2组工况(uf=1.24 m/s、um=0.44 m/s )
图10为给定右侧气室流量为14 m3/h(气体流速为0.44 m/s),左侧流量为28 m3/h(流速为1.24 m/s)时,颗粒在挡板式流化床中的运动情况。同样抽样102 400帧数据,可以看出:颗粒的最大速度相比于工况1增大,但是颗粒的速度基本都小于0.9 m/s;一段时间内,颗粒速度也是恒定的。
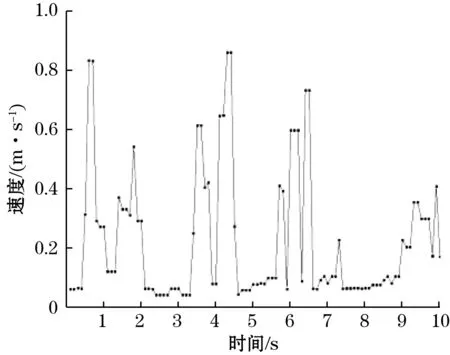
图10 第2组工况下流速-时间变化曲线
由工况1(图9)和工况2(图10)的分析可知,提高流化床中气体的流速可以提高介质运动速度,且在某一时间段内颗粒是流速维持恒定,但是介质最大速度比气体的最大速度要小,同时也反应了能量在不断地转移。
3.4 内循环流化床内质量流量的分析
在工况2的情况下对介质运动过程中的质量流量进行研究分析。由于传感器中挡板下方介质流过截面是50 mm×25 mm通道,介质的密度为1 640 kg/m3,所以由式6可以算出介质的瞬时M(t),如图11所示。
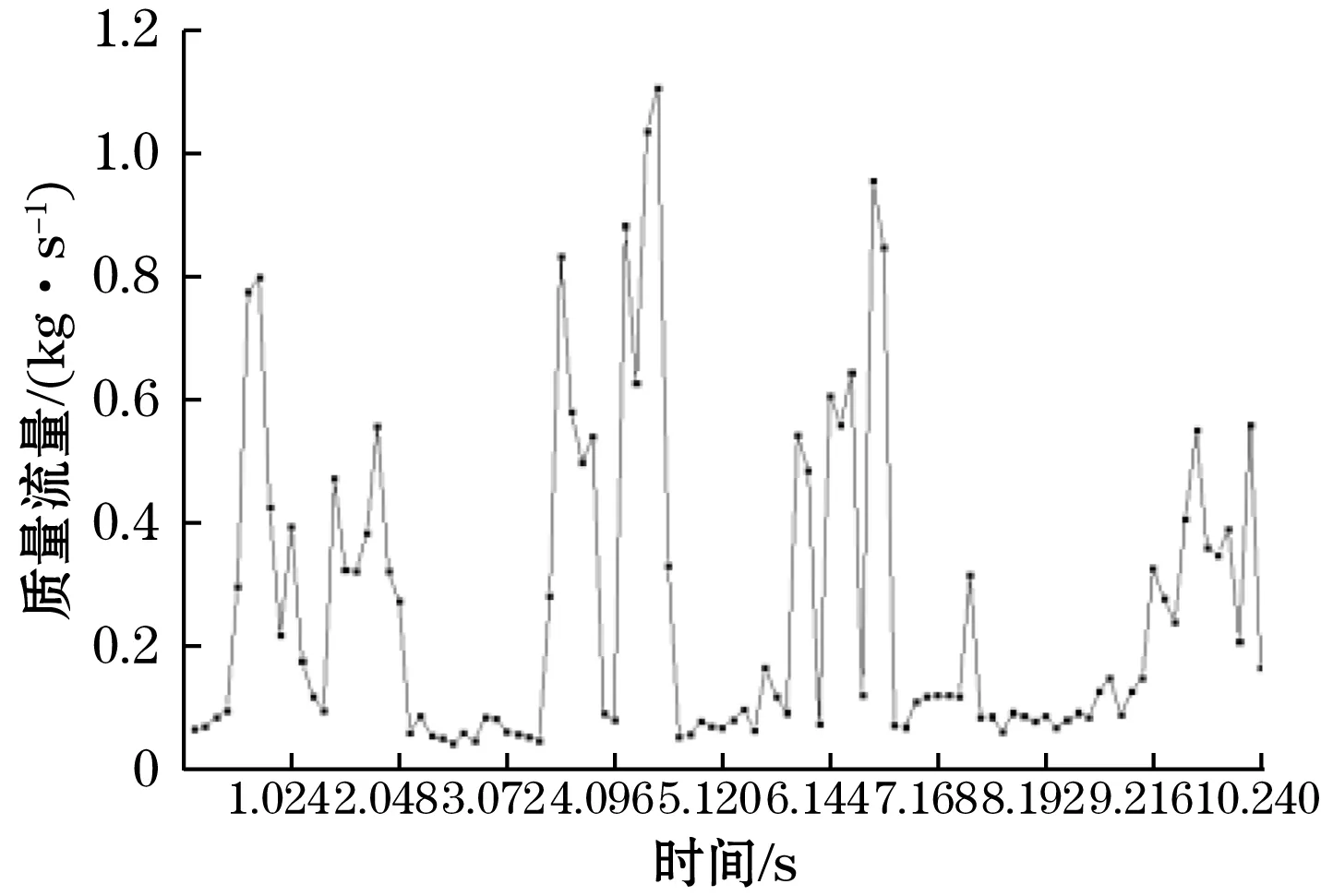
图11 瞬时质量流量
由图11可知,曲线走势与介质的流速曲线相似,但质量流量没有出现恒定的现象。因为当流化床中不断有气泡产生时,质量流量会随着鼓泡的大小和频率的变化而变化[12],所以后期仍需通过大量的实验分析,探索其中的具体规律。
4 结束
本文针对挡板式内循环流化床中气固两相流的流动参数检测设计了一套三电极的ECT系统,基于互相关算法,通过检测电容值实现了对床内介质参数的检测分析。对上、下游电极所采集的数据进行了一致性验证,并由上、下游的数据,算出了床内固相浓度情况;对比了2种情况下介质流速的规律,并计算出介质的瞬时的质量流量。实验结果表明,该系统可以准确地检测到床内动态参数的变化,为挡板式内循环流化床内动态变化研究提供又一有效途径。

