两类两招破系数

王苏文

(浙江省诸暨市浬浦中学 311824)

在二项式定理的考查中以二项展开式的系数问题为重点，根据所求系数可归为两类：单一型系数与多个型系数.单一型系数涉及含某项的系数、系数最大项、常数项等类型；多个型系数涉及每项系数、奇(偶)项系数、变式系数的运算等类型.一般而言，单一型系数用公式法可破解；多个型系数用赋值法可破解.

一、单一型系数问题

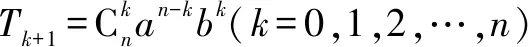
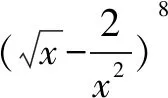
(1)含x3/2项的系数；

(2)最大的二项式系数为第几项；

(3)展开式中系数最大的项.

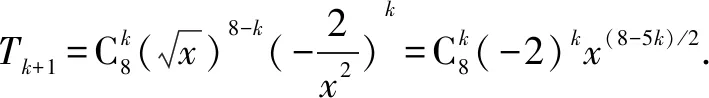
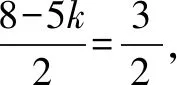
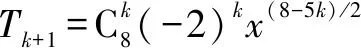
反思：①区别：项、第几项、项的系数、二项式系数等易混淆的概念，防止出错；②掌握系数最大与二项式系数最大的求解方法，尤其是系数有正负时可用绝对值优先处理；③掌握指数幂运算是二项展开式计算准确的关键.

例2已知x10+x2=a0+a1(x-1)+…+a10(x-1)10，求a8的值.

解将原式中的x→x+1，整理得：(x+1)10+(x+1)2=a0+a1x+a2x2+…+a10x10.

反思通过换元，巧妙地将问题转化为标准的二项式问题，换元可将问题进行归一，学会变通才能减少题海.

二、多个型系数问题

赋值法：根据所求系数的特征，合理进行赋值实现问题的解答.

例3已知(1-2x)8=a0+a1x+a2x2+…+a8x8，求:

(1)a1+a2+…+a8的值；

(2)|a0|+|a1|+|a2|+…+|a8|的值；

(3)a0+a2+a4+a6+a8的值.

解(1)根据条件，令x=1，得(1-2)8=a0+a1+a2+…+a8；令x=0，得a0=1.故a1+a2+…+a8=0.

(2)根据题意可知：a1,a3,…为负值，a0,a2,…为正值，可令x=-1，得|a0|+|a1|+|a2|+…+|a8|=a0-a1+…+a8=38.

反思通过所求系数的特征，常用x=±1,0等特殊值进行赋值，避免运用通项逐一求解的繁琐，实现问题的简捷化处理.

例4已知(x2+2x+2)5=a0+a1(x+1)+…+a10(x+1)10，求:

(2)a1+2a2+…+10a10的值；

(3)a0-a2+a4-a6+a8-a10的值.

解(1)令x=-1得：a0=1；

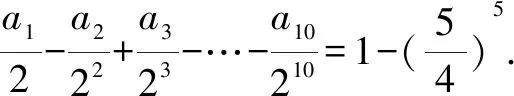
(2)结合系数，将原式两边分别求导得：

5(x2+2x+2)4(2x+2)=a1+2a2(x+1)+3a3(x+1)2+…+10a10(x+1)9.

令x=0得：a1+2a2+…+10a10=160.

(3)根据条件，令x=-1+i(i为虚数单位)得：

0=a0+a1i+a2i2+a3i3+…+a10i10=a0-a2+a4-a6+a8-a10+(a1-a3+a5-a7+a9)i.结合复数相等，可得：a0-a2+a4-a6+a8-a10=0.

反思通过对系数的特征分析找出适当的处理方法(如求导、复数)，探秘有效的赋值，为求解系数寻找一条完美捷径，让问题柳暗花明又一村.

二项展开式有关的系数问题，要抓住通项公式为重点与通法，巧妙运用赋值，可简捷有效地解决某些系数问题.