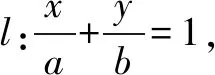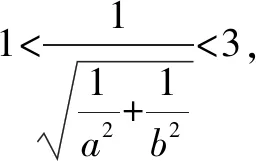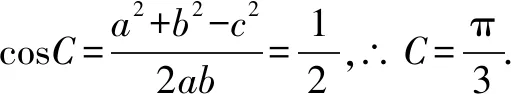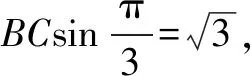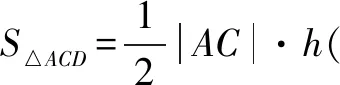试谈圆的穹顶性质及其应用

张俊畅

(广东省梅州市大埔县虎山中学 514299)

一、关于圆的穹顶

如图，过圆内一点作一条直线l，直线l交圆于A,B两点，直线l将圆分成两部分，其中一段为优弧，另一段为劣弧，过圆心作与AB垂直的直线l′，l′交圆于M,N两点，我们把点M,N称为圆的两个穹顶.

二、关于圆的穹顶的性质

在同类圆弧上的所有点P中，穹顶到切割弦的距离最大.记P到弦AB的距离为d，圆心C到直线l的距离为d0，圆的半径为r，则有：

①若在优弧AMB上任取一点P，则d≤d0+r，当点P在点M处时，d取得最大值；

②若在劣弧ANB上任取一点P，则d≤r-d0，当点P在点N处时，d取得最大值.

三、应用举例

1.判断圆弧上到定直线的距离等于定值的点的个数

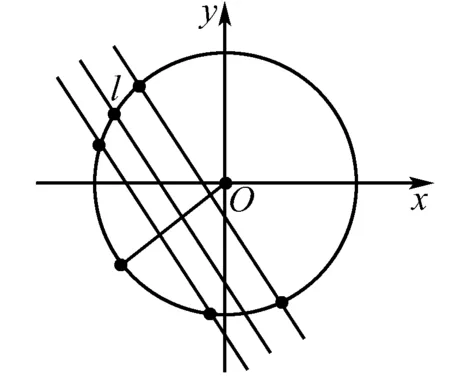
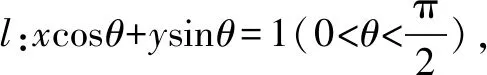
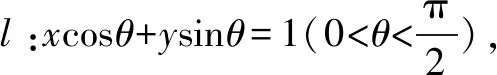
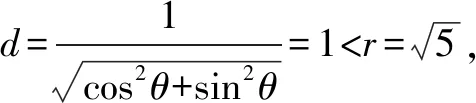
∴圆O上到直线l的距离等于1的点有4个.

解法提炼设⊙C:(x-a)2+(y-b)2=r2上一点到直线l:Ax+By+m=0的距离为d的点的个数为n，记圆C心到直线的距离为d0，则有：

① 当l与⊙C相离时，d0-r

若d>d0+r或d

②当l与⊙C相切时，0≤d≤2r.

若d>2r，则n=0；若d=2r或d=0，则n=1； 若0

③当l与⊙C相交时，0≤d≤d0+r或0≤d≤r-d0.

若d>d0+r,则n=0；若d=d0+r,则n=1；若r-d0

2.利用圆的穹顶性质求最值

例2已知△ABC的内角A,B,C的对边分别为a,b,c，且sin2A+sin2B-sin2C=sinAsinB，a=2,b=3,点D与点B位于直线AC的两侧，且BD=BC，求四边形ABCD面积的最大值.

∴(S四边形ABCD)max=S△ABC+(S△ACD)max

在教育实践中，我们要善于运用形式化原则进行恰当的数学建模，培养学生的抽象概括能力和数学表达能力.正如张奠宙教授所说：要重点培养如下三大意识：将数学关系、数学问题用符号恰当地加以形式化的意识；在形式系统中按操作规则推演时，随时注意关键处字母取值范围的变化，牢固把握符号的本真理解的意识；为形式关系、形式结构寻求对应的模型意识.对有疑惑的问题，我们抱着刨根问底的精神，努力探求问题的实质，总结其中的规律，我们就能对这类问题有一个比较清晰全面的认识，使我们的认识水平提升一个层次，领略到别人看不到的风景，许多困惑也能瞬间烟消云散.正如王安石的一首名诗所说的一样，“不畏浮云遮望眼，自缘身在最高层”.