小波自回归模型在天顶对流层延迟预测中的应用

李伟捷 ，刘根友

（1. 中科院测量与地球物理研究所 大地测量与地球动力学国家重点实验室，武汉 430077；2. 中国科学院大学，北京 100049）

0 引言

全球卫星导航系统（global navigation satellite system， GNSS）信号在对流层的传播过程中，会发生路径弯曲以及传播速率改变，导致信号接收端测距误差，即对流层延迟。对流层延迟误差与水汽、温度等因素密切相关，随卫星信号入射高度角减小而增大，在天顶方向约2.3 m，当卫星高度角降低到10°时，可达15～20 m[1-2]。对流层延迟是 GNSS卫星定位重要误差之一，提高对流层改正精度有助于模糊度固定和定位精度的提高。一般情况下，对流层误差可以用模型公式计算，传统的 Hopfield模型及Saastamonien模型需要实测气象参数的支持才能满足实际需求[3-4]，为摆脱对实测气象参数依赖，许多经验模型被相继提出[5-8]。其中，GPT2w 、IGGtrop_SH和GZTDS这 3种对流层延迟经验模型精度较高，内符合精度分别为3.6、3.8、3.7 cm[9-11]。由于天顶对流层延迟（zenith tropospheric delay，ZTD）及相关气象因子显著的年及半年周期特性，这几种模型的参数均是由频率f1=1/365.25和f2=2/365.25的谐波函数表示，这种表示的方法简单有效，有利于全球格网的建立。同时，文献[12]基于小波分析发现，对流层延迟的噪声主要集中在低阶高频部分，而通过小波提取的低频部分能较好地保留有用信息。为了提高单站对流层误差预测精度，本文在考虑周年和半年谐波项的同时，还将利用小波分析提取剩余残差的低频部分，并对相对平稳的低频信号建立自回归模型。

1 基本理论

1.1 谐波函数拟合

由于单站 ZTD序列具有显著的年周期及半年周期，通常通过频率为f1=1/365.25和f2=2/365.25的谐波函数对单站进行拟合[8]，其计算方法为

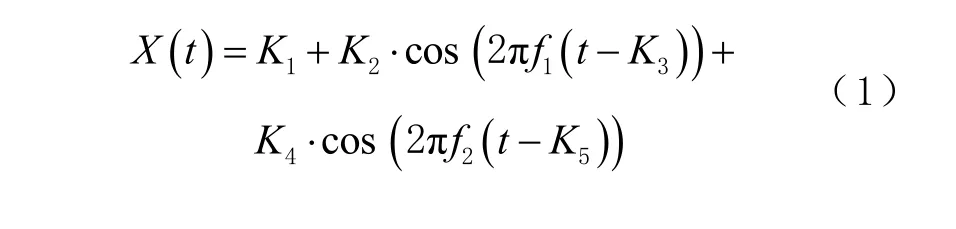
式中：t为简化儒略日，即与1980-01-06零时即全球定位系统（global positioning system，GPS)时零点对应儒略日（2 444 244.5）的差值；X(t)为t时刻的对应ZTD的值；系数Ki通过最小二乘法确定。

1.2 离散小波变换

离散小波变换是通过低通和高通2个互补的滤波器将信号分解成a和d2个部分，a为信号的近似值（approximations），d为信号的细节值（detail）[13]。在地球物理邻域，该法常用于分析含有多尺度特征、奇异值检测以及瞬态现象的非平稳信号[14]。本文采用小波分解树形式，只对低频信号进行继续分解，对应公式为原始信号，j为分解阶数。其中，图1为3阶分解，则有S=a3+d3+ d2+d1。

图1 离散小波变换原理

1.3 自回归模型

自回归模型（auto regressive model，AR）模型是将t时刻输出表达成过去时刻输出序列的线性组合[15]，是一种利用序列自相关特性建立的线性预测模型，模型阶数n根据贝叶斯信息准则BIC及系数显著性确定[16]，其计算方法为

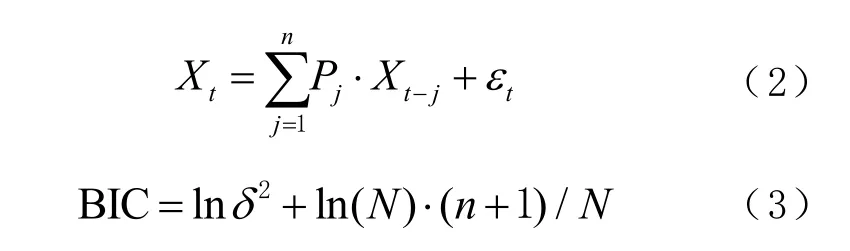
式中：Xt为t时刻的值；ɛt为拟合残差；系数Pj通过最小二乘估计；BIC为贝叶斯信息值；n为模型阶数；б2为拟合残差方差；N为样本数。

1.4 小波及自回归组合模型（wavelet-autoregressive model, WAMIX）实施流程

本文结合谐波函数拟合、离散小波变换以及自回归模型3种手段，通过对已知数据的建模，实现对流层延迟的预测。具体步骤如下：

采用谐波式（1）拟合，提取ZTD的主要趋势项（年周期及半年周期信号）；通过小波把上一步残差结果分解成低频及高频分量，挖掘各分量的变化特性，选择合适阶数，将高频分量作为噪声剔除并保留低频分量；对保留的低频信号建立适宜的 AR模型，实现时序预测。具体流程如图2所示。

图2 WAMIX建模流程

2 实验与结果分析

2.1 数据来源

对流层延迟数据采自国际 GNSS服务组织（International GNSS Service，IGS）数据共享平台ftp：//cddis.gsfc.nasa.gov/，该平台提供了高精度的天顶对流层延迟ZTD，采样间隔为300 s。本文选取了2013年1月1日至2016年12月31日数据完整率达90 %的ARTU、BJNM、DRAO、GODE、LHAZ、 KOUR、YELL等7个测站作为研究对象。选用每天中午12时的数值为当日值，并通过样条插值得到等间隔为1 d的数据，测站分布如图3所示。

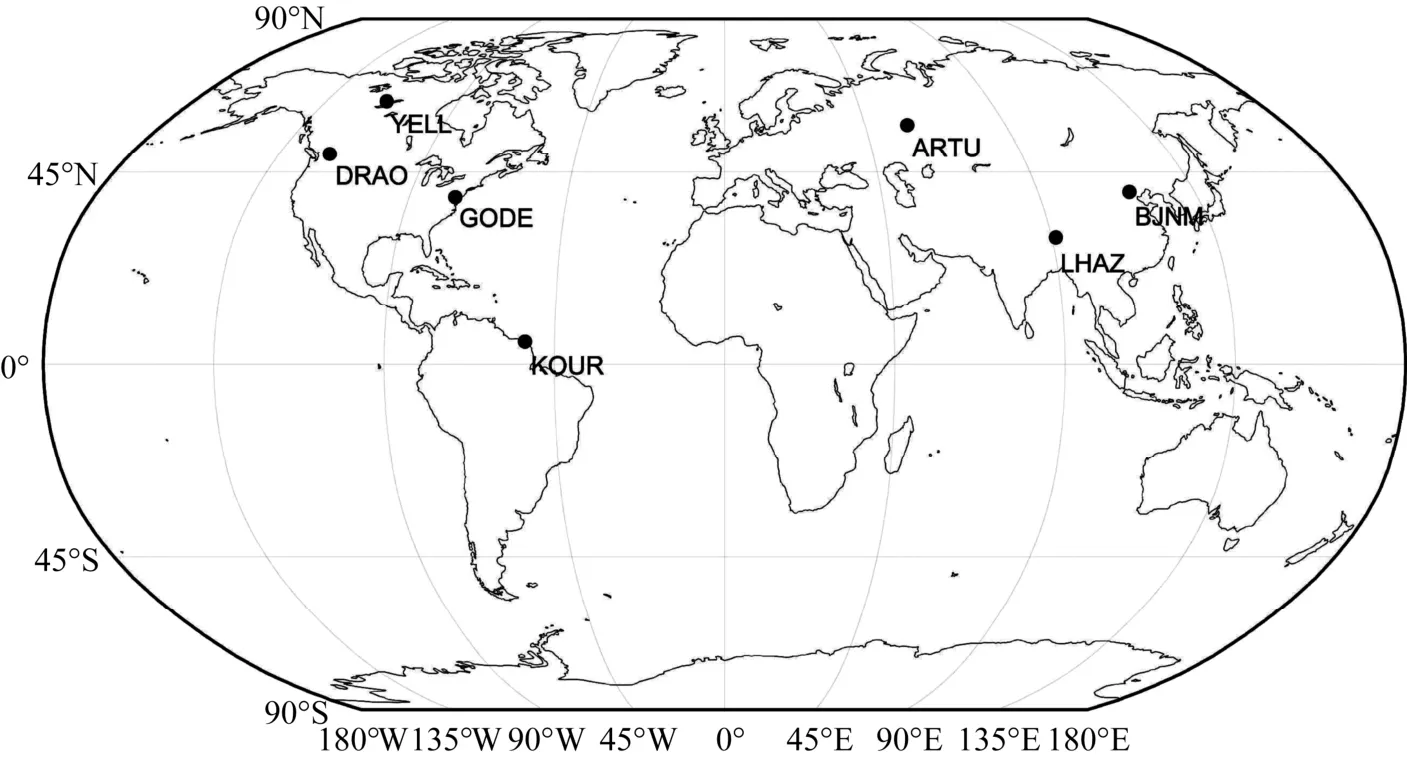
图3 选用测站分布

2.2 方法与结果

首先利用2013—2016年全时段数据，通过快速傅里叶变换(fast Fourier transform，FFT)分析存在明显的周年项和半年项，因此可以根据式（1）提取出各站ZTD序列中主要趋势项年周期及半年周期，如图4（鉴于篇幅，仅列出ARTU和BJNM站）所示。然后对观测值减去谐波拟合后的残差进行 db45小波 10阶分解。文献[12]中提到，ZTD小波变换前几层高频分量主要是由测量、仪器、天气或人为原因等引起的误差，因此，本文参考图5的小波信号分解，保留相对平稳的a4分量进行AR建模，其中a1～a10表示 10 阶分解得到的低频分量，d1～d10对应的是高频分量，a4中包含的为 16 d及更长时段对应低频信号。建模对象为4组150 d连续样本（2014和 2015年年积日第 1～150天及年积日第 51～200天），根据 BIC准则及系数显著性，AR模型定阶为11。最后，对样本区数据进行一步预测检验并采用通过检验的AR[11]模型预测后30 d的结果，与观测值进行比较，统计其精度，其结果见图5至图7。

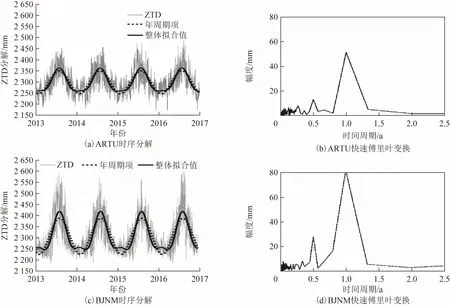
图4 ARTU及BJNM站ZTD时间序列及其谐波函数拟合图

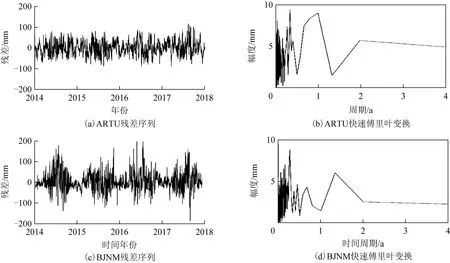
图6 ARTU及BJNM站谐波拟合残差及其傅里叶变换频谱分析结果

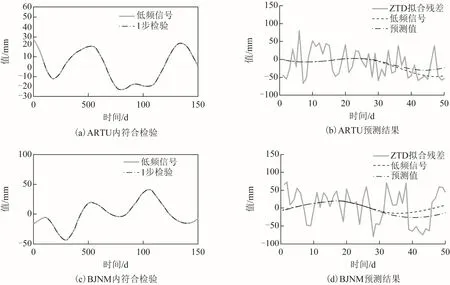
图7 ARTU及BJNM站低频分量AR模型预测结果

图 5 至图 7 的（a）、（b）和(c)、(d)分别对应 ARTU和BJNM 2014年第1～150天a4低频分量预测结果，（a）、（c）为样本区内一步预测检验，（b）、（d）为样本区外预测结果。

为验证模型预测精度，本文将 WAMIX模型与目前认可精度较高的GPT2w(1°×1°)和IGGtrop_SH进行精度对比，以IGS站提供的ZTD为真值，计算各模型序列残差，统计其均方根误差(root mean square， RMS)和平均相对中误差（average absolute relative error， AARD）。据预测结果统计（表 1至表4），GPT2w 的 RMS 为 36.7 mm， AARD 为 1.3 %；IGGtrop_SH的RMS为 36.6 mm， AARD为 1.3 %；WAMIX的 RMS为 30.5 mm， AARD为 1.1 %。前二者精度相当，WAXMIX较之精度有所提高，RMS平均改善6 mm，AARD改善0.2 %。4组预测数据中，最佳结果是2016年8月LHAZ预测，较 GPT2w模型 RMS改善 28.7 mm，AARD改善1.5 %，较 IGGtrop_SH模型RMS改善20.2 mm，AARD改善1.1 %。

对比 2014年及 2015年的预测结果时发现，2014年 WAMIX预测精度低于 2015年，尤其是在2014年6月，GODE站及KOUR站的RMS较GPT2w及IGGtrop_SH分别大了7和2 mm。为分析误差来源，本文还纳入了式（1）谐波拟合的精度结果，发现这2站WAMIX预测结果不及谐波，同时，在ARTU及BJNM站出现类似问题，但在图6（b）、图6（d）中预测值和样本低频分量a4基本吻合。因此，本文推测这不是 AR模型本身拟合的问题，而是由于建模时未考虑高频分量造成的。

表1 2014年6月预测精度统计

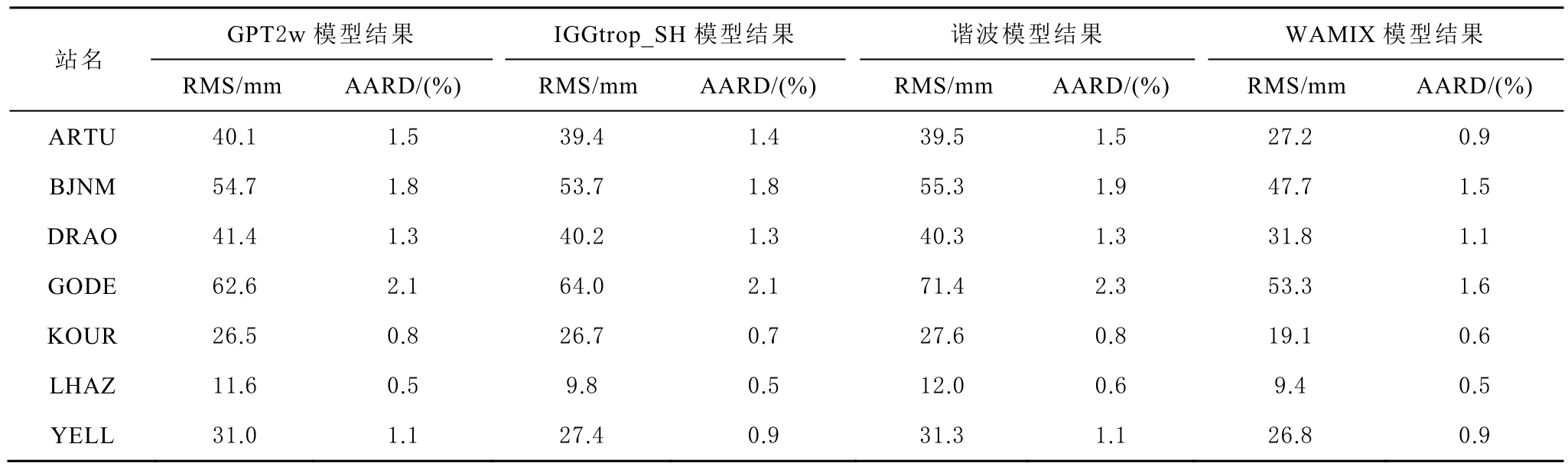
表2 2014年8月预测精度统计

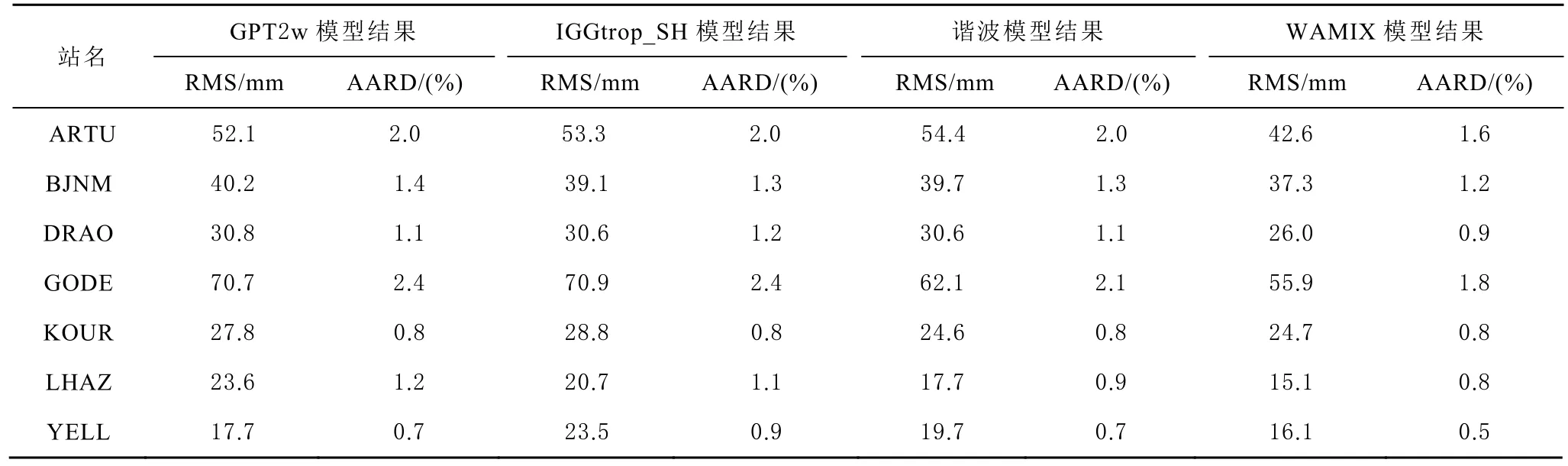
表3 2015年6月预测精度统计

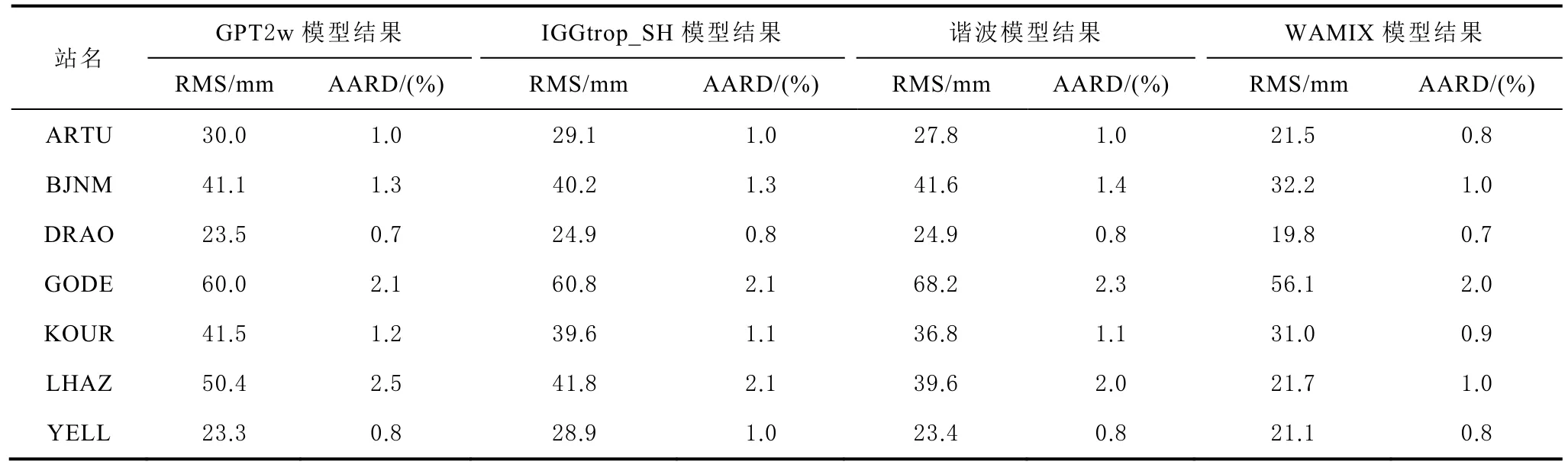
表4 2015年8月预测精度统计

高频信号中除噪声外，还包含 ZTD真实信号受气象影响产生的高频分量，其主要影响因素是水汽，温度以及气压[8]。据本文获取的气象资料记载，北京2014年6月气候多变且昼夜温差较大，陆续出现了16 d降雨，其中含15 d雷阵雨。由此产生的水汽和温度的强烈变化会直接导致ZTD不稳定，产生大量高频信号，对前文的推测予以佐证。相反，精度效果改善最佳的 LHAZ站，地处中国西部降雨偏少且海拔较高，高频信号相对稳定。由于缺乏其他站的气象数据，具体的产生原因还有待进一步验证。

3 结束语

本文基于IGS 7个测站4 a（2013—2016年）的ZTD数据，采用一种小波-AR组合模型WAMIX实现单站建模预测，采用全时段数据进行谐波拟合和小波分析，在此基础上利用150 d的低频分量预测后 30 d的数据。WAMIX的预测精度为：RMS：3 cm， AARD：1.1 %，较 GPT2w和IGGtrop_SH模型整体精度为好，RMS平均改善6 mm，AARD改善0.2 %，RMS最优改善2 cm，AARD最优改善1 %。在气象稳定区域，ZTD真实高频分量较小，模型效果较好；在天气多端甚至异常区域，高频分量不能完全作为噪声处理，模型效果可能不佳，需要综合其他气象资料进一步研究。