亚波长纳米金属光栅偏振聚光器设计*

关 乐， 王忠旭， 李世奇， 刘 胜， 崔 岩， 褚金奎

(1.大连理工大学 精密与特种加工教育部重点实验室，辽宁 大连 116023;2.辽宁省微纳米技术及系统重点实验室，辽宁 大连 116023)

0 引 言

导航技术在人类活动中具有重要的作用，近年来，基于天空光偏振分布模式图并以太阳子午线为基准来获取方向信息的新型偏振导航方法成为了研究热点[1～6]，偏振光导航定位功能在军事和民用领域具有广泛的应用价值。

目前,国内外已有的偏振导航器件大多都是以Cataglyphis的沙蚁[1]作为仿生学设计原理，采用基于偏振对立(polarization opponent，POL)神经元模型算法[8]，通过计算反正切函数求解偏振相位角，得到传感器参考轴与太阳子午线夹角，再与太阳方位角“求和”来进行导航应用。根据沙蚁利用视网膜神经感杆对天空中偏振光敏感的原理，本文提出了仿生视觉光电传感器，针对传感器中最为重要的偏振器件，采用了亚波长金属偏振光栅，克服了利用传统天然晶体双折射效应制作的偏振器件体积过大，价格昂贵的局限性，其偏振性能的偏振性优于二色性薄膜偏振片，且与微系统(micro-electro-mechanical system,MEMS)工艺有着良好的兼容性。目前使用了金属光栅偏振器的偏振光导航传感器的室内精度达到了±0.1°[9]。已研制的原理样机仅能应用于日光环境下，为提高系统使用范围，尤其是夜间等微光环境下，以达到全天候使用的要求，面向夜晚微弱光环境应用的仿生偏振微纳导航传感器亟待设计。

对昆虫复眼的结构和功能的研究表明，蜣螂等夜行性昆虫通过其复眼结构实现光的聚焦增强作用[10，11]。国防科技大学张军等人总结了昆虫复眼的仿生研究进展，指出了目前通过光刻玻璃对昆虫复眼进行仿制存在的优缺点，威斯康辛大学的Beebe D J等人[12]利用对光敏感的水溶胶材料制作了可以自主调焦的微透镜，上述两种结构的仿昆虫复眼透镜属于传统光学透镜范畴，分辨率低，且难以满足偏振导航传感器中的集成制作。为突破衍射极限、实现超分辨成像与聚焦，基于表面等离子的平面金属透镜提供了一种新的技术实现手段，其可使作为倏逝波的表面等离子体参与成像，因此,基于纳米圆环或圆孔等金属纳米结构的平面金属透镜得到了广泛研究[13～29]。亚波长圆孔式平面金属透镜[29]、蝴蝶结型平面金属透镜[30～33]都拥有良好的聚焦性能，但其工作距离仅有10 nm，难以完全达到偏振光导航传感器的应用需求。中科院罗先刚等人利用变宽度的纳米狭缝阵列使光通过纳米狭缝后产生相位延迟，进而实现聚焦的功能[34]，哈佛大学 Federico Capasso团队利用纳米纤维结构设计了可以消除色差，在可见光范围内实现全波段聚焦的超透镜，其通过优化纳米纤维的形状、宽度、间距及高度，就可以聚焦不同波长的光[35]。

为实现原有偏振光传感器在微光环境下的应用，本文在本课题组对纳米金属光栅的研究基础上，结合纳米狭缝式平面金属透镜，设计了一种可以实现聚焦功能的纳米金属光栅偏振聚光器，该偏振聚光器由6个结构相同，方向不同的偏振聚光器件组成，采用时域有限差分(finite-difference time domain,FDTD)方法对不同结构参数下的偏振聚光器件进行了数值模拟，对结构参数的影响规律进行了系统的分析，对偏振聚光器件的透射率及消光比进行了计算。

1 基本原理

1.1 六方向亚波纳米金属光栅偏振器原理

如图1(a)所示为沙蚁偏振视觉系统中的偏振敏感神经感杆结构，由1～7共7个细胞组成，每组细胞中均含有微绒毛结构，其通过正交的微绒毛结构采集偏振光信息[36]，图1(b)为本文设计的偏振光导航传感器的偏振信息采集模块结构示意[9]，其相当于对昆虫的微绒毛结构进行了仿生设计，该传感器由3组正交偏振传感部件组成，3组部件位于同一个平面上，6块偏振器件具有完全相同的结构参数，仅安装角度不同，为此本文只对一块偏振器进行仿真分析即可。每组部件的2个单元产生2组电流信号，将这2组电流信号通过对数放大器得到电压信号，最终将使用2组电压信号解算出偏振度和偏振角，而采用3组部件则可以通过增加冗余的电压通道提高传感器灵敏度。

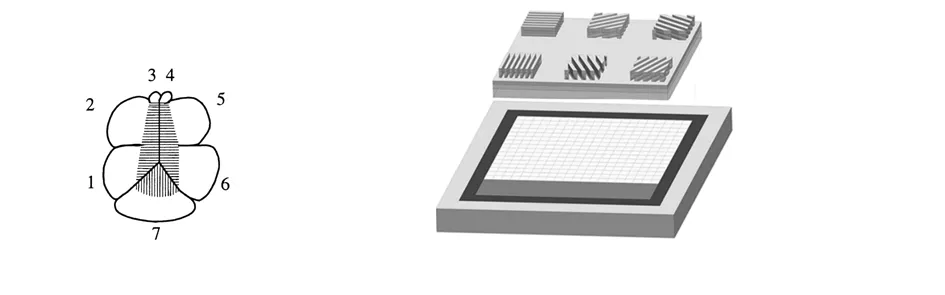
图1 基本结构

目前安装了此偏振器的偏振导航传感器的室内精度可以达到±0.1°，室外精度可以达到±1°，但室外实验表明，在夜间20∶00之后的微光环境下，传感器无法输出准确的信息,本文在保留原有六方向光栅结构优势的基础上，设计了聚焦亚波纳米金属光栅偏振器。

1.2 聚焦平面金属透镜原理

聚焦平面金属透镜利用特殊结构调控光的相位，控制不同位置出射光的相位延迟，即可使出射光的方向产生一定的偏转来实现聚焦的目的。其原理如图2所示，图中d为金属层的厚度，相邻金属的距离w记为狭缝的宽度。

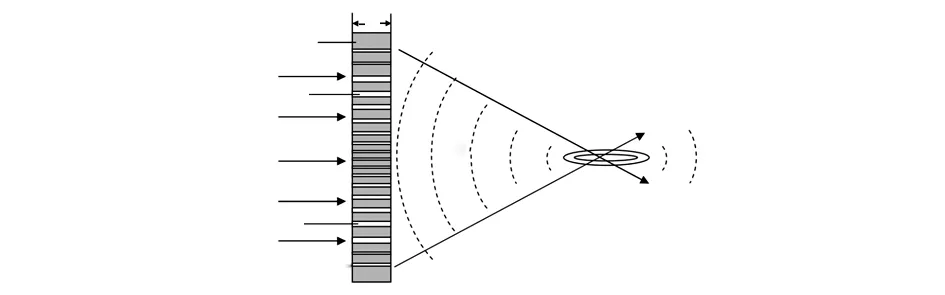
图2 聚焦平面金属透镜原理示意[34]

光线通过平面金属透镜后的相位Φ(x)的计算公式为

(1)

式中Φ(0)为在x=0处的光栅出射界面处的出射光的相位，Φ(x)为在x处的光栅出射界面处的出射光的相位，n为整数，λ为光在真空中的波长，θ为出射光线的偏转角度(越大出射光的聚焦位置离光栅越近)。

假设到达光栅入射界面处的光的相位相同，出射界面处的出射光的相位

(2)

式中 ΔΦ1为入射界面处的相位延迟，ΔΦ2为出射界面处的相位延迟，Φ为入射光的相位，kspp为狭缝中传播的等离子波的波矢(其值与光栅缝宽和狭缝内介质的折射率有关)，d为狭缝的厚度

ΔΦ1=arg(r1),ΔΦ2=arg(r2)

(3)

(4)

根据罗先刚团队的研究[9],当狭缝的宽度大于10 nm时，式(2)中参数Φ的影响比参数ksppd的1 %还要小，而当光栅上下表面的介质的折射率相同时r1和r2大小相同,方向相反，则ΔΦ1+ΔΦ2，式(2)简化为[35]

ΔΦ=ksppd+Φ

(5)

根据式(4)、式(5)可知，通过改变纳米金属狭缝的高度d、宽度w，可以对光透过结构后的相位角进行调控，为此本文将针对金属高度d和狭缝宽度w，设计相应的结构参数及参数变化方式，以探究其对光场聚焦的规律。

2 参数设计与仿真分析

2.1 纳米金属光栅偏振聚光器金属层高度d的仿真

为提高仿真效率，考虑到6块偏振器件除分布角度外完全相同，可将单块偏振器件结构简化为二维结构进行分析。对纳米金属光栅偏振聚光器金属层高度d的探究中，本文设计了如下3个参数：金属层的高度起始值即最小值d、两个相邻金属层高度按照线性规律变化时的一次项系数dd以及高度按照抛物线规律变化时的二次项系数da。将具有不同参数的偏振聚光器采用FDTD方法进行数值模拟，将光透过偏振聚光器后的场强数据进行导出处理可得到图3。

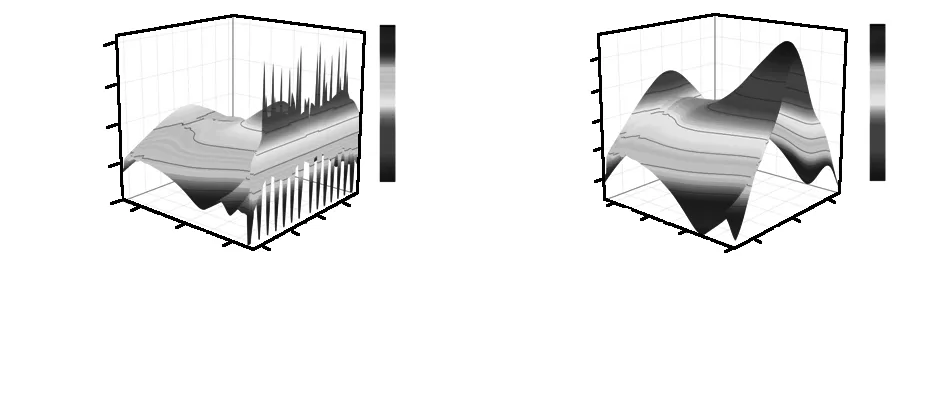
图3 仿真结果

图3(a)是对仿真后光场分布图电矢量E进行数据提取和分析，其中的“毛刺点”由表面等离子体激元现象导致的近场聚焦点，这些数值峰值点会干扰后续对峰值点的坐标及数值的查找和再处理，故需要将这些峰值数据过滤，得到如图3(b)。

对过滤后的数据进行处理，得到各结构下焦点位置坐标及相对电场强度值，如图4。其中，不同的金属层起始高度中，一次项系数对聚焦位置和聚焦效果的影响为光栅存在最佳金属层高度范围100～400 nm，在此范围内的光栅结构具有聚焦功能，并有一定的变化规律；在最佳变化范围内，随着一次项系数数值的减小，聚焦效果逐渐增强且焦点位置逐渐向光栅位置偏移。

图4 一次线性规律不同高度起始值中一次项系数数值对聚焦位置

图3和图4的数据结果证明了本文设计的偏振聚光器能够有效地实现光的聚焦功能，在此基础上，本文将偏振聚光器对可见光中不同波段的透射率及消光比在FDTD Solutions 中进行了解算，如图5。

图5 一次线性规律中不同结构参数下的透射率

从图5中可以看出，设计的偏振聚光器在450 nm左右的蓝色光波段具有较好的TM光透射率，符合本课题所设计的对450 nm左右波段敏感偏振光导航传感器。在此基础上，本文又计算了TE偏振光的透射率和消光比，不同参数下的消光比如图6所示。

图6 一次线性规律中不同结构参数下的消光比

对于金属层高度按照二次线性抛物线规律变化的情况，进行了同样的分析并得到如下结论：

在不同的起始金属层高度中，二次项系数对聚焦位置和聚焦效果的影响：光栅存在最佳金属层高度范围100～400 nm，在此范围内的光栅结构具有聚焦功能，并有一定的变化规律；在最佳变化范围内，随着二次项系数数值的减小，聚焦效果逐渐增强,并且焦点位置会逐渐向光栅方向偏移。

同样，本文分析了二次抛物线规律中不同结构参数下的TM透射率，如图7。由于能产生聚焦效应的金属层高度上限约为400 nm，故部分起始值较大的结构中，二次项系数da不能过大。

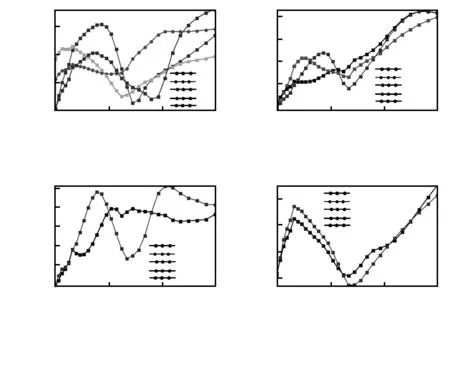
图7 二次抛物线规律中不同结构参数下的透射率

图8(a)和图8(b)分别是等差规律变化和抛物线规律变化中最佳结构的E矢量仿真结果，数据显示其焦点处的电场强度分别增加到了约为3倍和4倍，根据光强值与电场值的平方成正比的关系，通过计算可以得出焦点处的光强增加到了9倍和16 倍，其焦点位置约为2 964 nm和2 798 nm。

图8 2种规律变化中最佳结构的仿真结果

2.2 纳米金属光栅偏振聚光器金属狭缝宽度w

与上述对金属光栅偏振聚光器金属层厚度d的设计分析类似，在对纳米金属光栅偏振聚光器金属狭缝宽度w的仿真分析中，对如下3个参数进行了对比仿真：相邻狭缝间的距离w、两个相邻狭缝的高度按等差规律变化中的等差值wd以及抛物线变化中的二次项系数wa。仿真结果表明，缝宽太小或太大，都无法实现聚焦功能，存在最优的缝宽范围，其数值为200～400 nm；在缝宽不同的变化方式中，若缝宽线性变化，当一次项系数wd的数值增大时，其聚焦效果越强；若缝宽按照抛物线规律变化，则随着二次项系数的增加，其聚焦效果越强。图9(a)和图9(b)分别是等差规律变化和抛物线规律变化中最佳结构的E矢量仿真结果图，数据显示其焦点处的电场强度分别增加到了约为1.2倍和1.3倍，根据光强值与电场值的平方成正比的关系，可以计算得出焦点处的光强增加到了1.44倍和1.69倍。

3 结 论

本文设计了聚焦亚波长纳米金属光栅偏振聚光器，在偏振聚光器变狭缝宽度和变金属高度两种形式下，采用FDTD方法对其结构参数进行了数值模拟，并给出了各设计参数对聚光器焦点位置及聚焦效果的影响，分析结果表明:纳米金属光栅偏振聚光器的狭缝宽度和金属层高度存在一个合理范围，分别为100～400 nm和200～400 nm；金属层高度增加的越慢，即一次线性变化中dd和二次抛物线规律变化中da越小，聚焦效果越强，焦点位置越靠近金属光栅偏振聚光器；狭缝宽度增加的越块，即一次线性变化中wd和二次抛物线规律变化中wa越大，聚焦效果越强，焦点位置越靠近金属光栅偏振聚光器；最优结构参数下，焦点位置位于偏振聚光器光出口2 798 nm，光强值提高到了16倍，450 nm的导航器敏感波段透射率约为63 %。本文为未来集成光路中的纳米结构器件的设计以及解决偏振光导航系统全天候尤其是在微光等环境下应用的问题提供了新的思路。