压电测力仪的联立标定方法研究*

张 军， 宋 鹏， 任宗金， 李明昱

(大连理工大学 机械工程学院，辽宁 大连 116023)

0 引 言

压电测力仪具有高固有频率、高灵敏度、线性度好、滞后和重复误差小等优点[1]，广泛应用于切削力监测[2]、设备操作载荷测试[3]以及航空、航天装备研制[4]和推力检测[5,6]等领域。这些领域一般采用四点及以上布置方式的压电测力仪作为核心测试环节，来实现力矢量的高精度测量。标定作为测试前的重要环节，直接影响测试精度，因此提高标定精度十分重要。对于四点及以上布置方式的压电测力仪，由于过定位约束，力解耦困难，造成了测力仪标定困难。而静态标定方法的选择决定了测力仪的标定精度。

文献[3]通过标定解耦矩阵，实现对一种新型轴用并联压电式六维大力传感器的标定。陈修平[7]通过正交加载并调整电荷放大器灵敏度，完成测试系统的归一化标定。Wright A M 等人[8]对每个测力臂单独进行标定，实现了六分力测力平台的标定。齐亚洲等人[9]提出输出比例归一化法的静态标定，降低了偏载对压电传感器多维力测试精度的影响。这些标定方法解决了力解耦困难，但局限于保证单个标定点处的高测试精度，并没有研究在非标定点处的测试精度。在实际测试中，力实际作用点往往远离标定点，造成测力仪受力状态与标定时不一致。尤其是主向力测试中，作用点变动范围更大，主向刚度较小，采用这些标定方法呈现出测试误差随测试点到标定点的距离增大而增大的现象，甚至出现误差超差[10]。

本文以四支点压电测力仪的主向标定为例，提出联立标定法，解决了力解耦难题。基于测力仪测试模型，构建主向力电关系方程组，求解主向力电转换系数。对标定方法进行扰动分析和误差分析，建立力电转换系数的误差界限模型。同时在测力仪上表面远离标定点的位置，进行了加载实验，计算并分析测试力值及其误差，研究误差在测力仪上表面的分布情况。

1 测力仪测试模型

四支点压电测力仪结构如图1所示，由4个同一型号的三向压电力传感器(3)、上板(2)、下板(4)、预紧螺栓(1)以及绝缘电缆等组成。四支点压电测力仪主向受力模型如图2所示。O′x′y′z′为矢量力坐标系，位于测力仪的上板上表面。Oxyz为测力仪坐标系，经过力传感器物理中心1,2,3,4。当力Fz作用在测力仪上板O′x′y′时，4个压电三向力传感器处主向受力为Fzi，产生输出Ui，满足力电关系式

Fzi=ciUi(i=1,2,3,4)

(1)

Fz=c1U1+c2U2+c3U3+c4U4

(2)

式中ci为第i号压电三向力传感器的主向力电转换系数；力电转换系数由力传感器自身决定，选定电荷放大器参数后，其值不再发生变化。

图1 压电测力仪爆炸图

图2 压电测力仪受力模型

2 标定方法与扰动分析

四支点约束属于超静定，测力仪受到标定力作用时，各个力传感器的受力难以解耦，给标定带来了困难。

标定点位置不同，力的分配比例不同，通过选取4个不同标定点处的力电关系式，组成四元一次方程组，就可求解出主向力电转系数。这种方法就是联立标定法。由式(2)得到算子方程

Uc=F

(3)

即

式中Fjz为第j点标定时，测力仪受到的主向力值，单位N；Uji为第j点标定时，第i号压电三向力传感器的主向输出电压值，单位V。

当|U|≠0时，算子方程有唯一解；当|U|=0时，算子方程无解。

另外，在实际测量中，由于标准测力环误差、加载力偏斜和加载误差等因素会产生ΔF。当右端阵有各种扰动ΔF时，则

c+Δc=U-1F+U-1ΔF

(4)

(5)

若U存在U-1，则算子U的条件数为

k(U)=‖U‖*‖U-1‖

(6)

有以下条件数不等式

(7)

在实际测量中，由于电荷泄露、电荷放大器误差和采集卡误差等因素会产生ΔU，当系数矩阵U有各种扰动ΔU时，则

c+Δc=(U+ΔU)-1F

(8)

有以下条件数不等式

(9)

当ΔF，ΔU均扰动时，则

c+Δc=(U+ΔU)-1F+(U+ΔU)-1ΔF

(10)

当‖U+ΔU‖<1时，有以下条件数不等式

(11)

从式(7)、式(9)和式(11)可以估算出算子方程(3)的近似解与真解的相对误差的上下界。当算子的条件数越小时，估计误差范围越小，近似解更能反映真解的情况。因此,标定点的选取原则是算子的行列式不为零且构成算子的条件数小。由经验，联立标定法选取4只力传感器轴线通过的点作为标定点时，条件数最小。

对于联立标定法，由于标准力偏差和数据采集误差以及电荷泄露等问题，导致主向力电转换系数的求解存在误差，从而使解得的主向力存在测试误差，误差传递函数为

ΔFz=U1Δc1+U2Δc2+U3Δc3+U4Δc4

(12)

式(12)表明:测试误差是连续函数，只受力电转换系数求解误差影响，若算子条件数小，则测试误差在测试面域内都很小。

3 加载实验

3.1 实验系统

如图3所示，通过多维力/力矩加载设备和标准测力环，完成对四支点式压电测力仪的主向加载。4只力传感器的主向输出，分别连接Kistler电荷放大器5018，经美国DataTranslation9804高速数据采集卡和Dewesoft 6标定软件显示输出信号。

图3 多维力/力矩加载设备

采用间隔采样方式对4路主向输入信号进行“并行”采样。各部分设备仪器参数如下：百分表式测力仪93618，量程6 kN，重复性误差0.07 %，温度修正系数0.00027/℃；Kistler电荷放大器5018，电荷灵敏度系数设为4.00 pC/N，量程5 000 N。数据采集卡DT9804，采样频率≥10 kHz。Dewesoft 6采样频率1 kHz。

等力值下，压电测力仪输出是关于作用点位置坐标的连续函数。可以选取均匀分布的加载点作为特征点，评估主向力在测力仪上表面内的测试精度。从对角线和对边中点连线上，共选取21个加载点，相对位置如图4所示。分别在21个加载点处施加主向(Z向)载荷，加载采用“逐级加/卸载法”，加载梯度是1 000,1 500,2 000,3 000,4 000,5 000 N，重复加载5次。

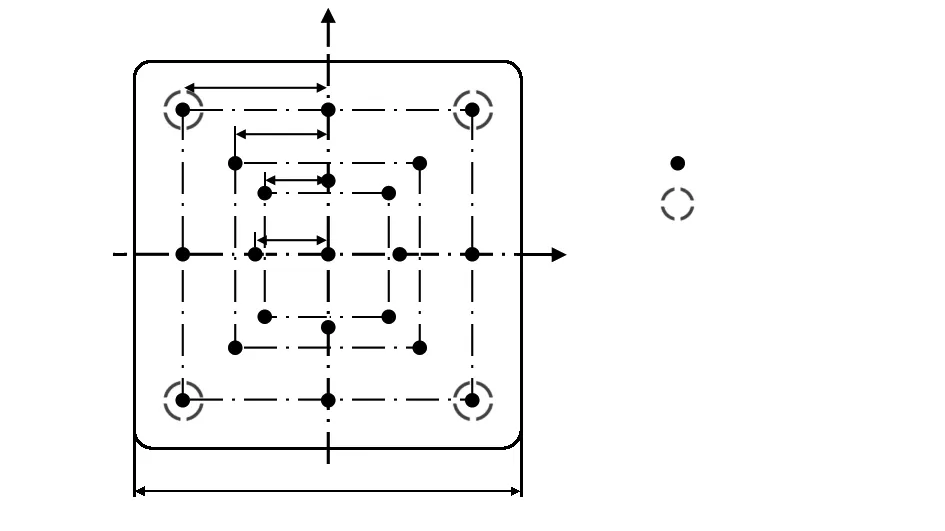
图4 加载点位置

3.2 试验结果分析

以4个支点(a1,a2,a3,a4)处5 000 N加载力下的力电关系式构成方程组，相应的算子条件数为1.4938，求解出力电转换系数c为(1.043,1.044 4,1.077 5,1.077 9)。

在21个加载点处，分别将4路主向输出电压和c代入公式(3)，得到各加载点主向合力测试值，并与理论值做差，得到误差范围，结果见表1。

表1 21个加载点处的主向力测试值及误差范围

从表1可以看出，在测力仪上表面，5 000 N量程范围内，联立标定法的主向力测试误差很小，其中最大绝对误差为18.8 N，对应的相对误差是0.376%。另外，压电测力仪的线性度和重复性由标定原始数据决定，不受主向力电转换系数的取值影响，本次实验中，压电测力仪的最大非线性误差为0.33 %，最大重复性误差为0.26 %。

如图5所示，加载力为5 000 N时，取21个加载点处的测试误差，拟合出测试误差在全面域内的分布图。可见，测试误差几乎不受加载点位置的影响。

图5 测试误差分布

4 结 论

基于测力仪测试模型和力的分配规律，提出了联立标

定法。构建力电关系方程组，求解力电转换系数，并进行了扰动分析和误差分析。同时在测力仪上表面，选取了21个均匀分布的加载点，进行阶梯力加载实验。对比分析了21个加载点处主向力测试值和误差分布。实验表明:在测力仪上表面，联立标定法的主向力测试误差都很小，最大误差只有0.376 %，说明联立标定法具有很高的测试精度，证明了该方法的可行性。