高空飞行环境中液体运载火箭底部热环境研究
周志坛,丁逸夫,乐贵高,梁晓扬,孙培杰,盛英华
(1.南京理工大学机械工程学院,南京 210094;2.上海宇航系统工程研究所,上海 201109)
0 引 言
近年来,随着载人登月、空间站组建、深空探测等一系列重大航天活动相继开展,我国加大了对重型运载火箭及其动力系统的研究工作,确定了液氧煤油发动机和液氢液氧发动机是运载火箭动力系统的最佳选择[1-3]。液体运载火箭发动机在工作时,由于外界环境压力过低,燃气流进入外界环境后急剧膨胀,在火箭底部形成回流,并对箭体底部形成对流加热效应,同时,高温燃气中喷射炽热的CO2和H2O等混合气流对火箭底部形成辐射加热效应[4]。火箭底部相当于背风面,容易受发动机喷流回流造成的对流加热与辐射加热耦合作用,导致温度迅速升高。对火箭底部热环境估计过低会给火箭整体的安全性带来极大威胁,甚至诱发爆炸等重大事故造成飞行失败,而估计过高又会导致热防护设备保守设计,增加发射成本[5-7],因此,对液体运载火箭底部进行热环境分析研究成为当前的重中之重。
国外已有大量学者对火箭底部热环境开展研究工作。1970年,Kramer[8]对泰坦III底部热环境进行试验测试,结果显示在刚起飞1 s内辐射热流是总热流的主要来源,随着飞行高度上升,辐射热流减少,对流热流升高;1994年,Reijasse等[9]对阿里安5进行数值模拟和缩比试验对比研究,得出影响对流热流的主要因素是飞行高度和喷管数量以及喷管排列方式;2007年,Negishi等[10]对H-IIA底部热环境进行数值模拟,结果显示底部热流峰值在30 km 高空附近。
近年来国内也有部分学者开展了喷流试验以及数值仿真方面的工作。史亚男[11]采用有限体积法求解RANS方程,湍流模型选取RNGk-ε两方程模型对火箭底部热环境进行仿真;周一鹏等[12]利用反向蒙特卡罗法计算火箭发动机喷管内的辐射热流;戴欣怡[13]采用标准k-ε两方程模型分析了液体发动机喷流对底部热环境的影响。
相比于国外对火箭底部热环境研究程度,国内目前还处于早期阶段,尤其是我国液体运载火箭飞行试验数据极少,国内学者对火箭底部热环境多为数值模拟方面的研究,缺乏对比分析导致仿真方法的有效性难以得到检验。并且由于计算资源有限,所以大多数学者对数值模型进行了不同程度简化,如几何模型只考虑四分之一、网格无边界层、热辐射计算中采用了精度较低的P-1模型等,这些都在很大程度上影响了计算精度。
随着计算机运算速度和内存规模飞速发展,为开展含边界层网格的结构化全箭三维流动数值模拟创造了有利条件。本文对液体运载火箭底部热环境进行数值模拟研究,在与试验测试完成对比验证基础上,通过大量研究分析不同飞行高度环境下,火箭底部热流的变化规律。
1 飞行试验
试验测试对象为某三级液体运载火箭,火箭共分为三个子级,由于液氧煤油发动机密度比冲高,因此一子级推进剂选择为液氧和煤油。在火箭底部放置两个热流传感器,传感器位置如图1所示。
测试结果为该火箭按照实际轨道飞行过程中,箭体底部两个热流传感器反馈的数据。

图1 火箭底部热流传感器位置Fig.1 The heat flux sensor of rocket tail compartment
2 计算模型
2.1 计算网格
采用多重网格方法对三维模型进行网格划分,该方法通过在不同疏密网格下求解原方程组,平顺高、低频误差,加速收敛过程。
为确保激波能够完整描述,对喷管及喷流区域网格进行加密处理,整个计算域均采用结构网格以保证网格的正交性及光顺性。在数值计算同时,为防止边界处的温度、压力等物理量变化剧烈,本文对边界层计算域的网格进一步加密,确保壁面附近网格Y+值小于3,具体如图2所示。
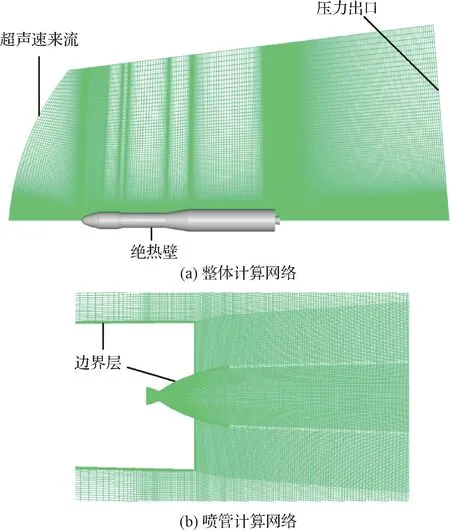
图2 计算网格Fig.2 Computational mesh
2.2 数值方法
2.2.1控制方程
基于液体运载火箭多组分燃气满足连续介质假设和理想气体状态方程的特点,建立三维多组分可压缩Navier-Stokes方程,包括质量、动量与能量输运的控制方程,形式如下。
多组分输运方程为:
(1)
式中:Yl为组分l的质量分数,Rl为组分l在化学反应后的净生成率,Sl为自定义源项的离散相引起的生成率。
组分扩散通量Jl可表示为:
(2)
式中:Dl,m为组份l的质量耗散系数,DT,l为组份l的热扩散系数。
在直角坐标系中,单一组分l的可压缩N-S方程的守恒形式为:
(3)
(4)
(5)
(6)
式(3)~(6)中:U为流动变量;F,G,H为气流通量矢量;Fv,Gv,Hv为黏性通量矢量;K为热传导系数;T为环境温度;p,ρ,e,τ,μ分别为压力、密度、比动能、应力、黏性系数;u,v,w分别为速度在x,y,z方向上的分量。
2.2.2空间离散格式
本运载火箭采用了大推力发动机设计方案,燃烧室总压、总温高,喷流速度为典型超声速,高空阶段箭体以超声速飞行,来流与喷流强烈干扰而形成复杂的发动机喷流效应,二阶迎风TVD格式收敛速度快,数值稳定性高,由于设计了鲁棒性强的通量限制器,不仅能求得高分辨率的复杂波系结构,而且抑制强间断解的非物理震荡,拟选用二阶迎风TVD格式计算全箭这类大型喷流模型。
将含箭体的整个计算域划分为六面体的结构化网格,采用有限体积法对每个体网格单元进行数值积分,流动变量U在体单元中心的体积平均为:

(7)
式中:Vi,j,k为计算体网格单元,采用二阶迎风TVD格式对对流通量进行离散。
(8)
其中,数值流通量分别为:
(9)
式中:λk,μk,νk为线性化替换矩阵的特征值;αk,βk,γk为线性化替换矩阵的展开项系数;ek(A),ek(B),ek(C)为线性化替换矩阵的特征向量,黏性通量采用二阶中心差分离散。
2.2.3湍流模型
湍流模型采用Realizablek-ε两方程模型,与标准k-ε两方程模型相比较,湍动耗散率ε方程中的产生项不再包含有湍动能k方程中的产生项Gk,并且湍动黏度μt中的系数Cμ不是常数,而是与应变速率相关,这样的形式能更好地表示能量转换。
湍动能k方程为:
(10)
式中:μ为混合物黏性,Gk为平均速度梯度引起的湍动能k的产生项,常数系数σk=1.0。
湍动耗散率ε方程为:
(11)
式中:常数系数σε=1.2;C1=1.44,C2=1.9,E为平均特征应变率。
2.2.4辐射模型
对辐射热流采用离散坐标法(DOM)进行求解,该方法具有易于处理散射问题,易于和流动方程联立求解以及计算精度较高的特点。该方法最早由Chandrasekhar[14]提出,由辐射传递方程沿着s方向进行离散得到:
在r位置沿着s方向的辐射传递方程为:
(12)
由式(12)可得光谱强度Iλ(r,s)的辐射传递方程为:
(13)
式中:r为位置矢量,s为方向矢量,s′为散射方向矢量,δ为气体层厚度,a为吸收系数,n为折射率,σ为黑体辐射常数,σs为散射系数,I为光谱辐射强度,T为黑体的热力学温度,Φ为散射相函数,Ω′为立体角,λ为波长,Ibλ为普朗克方程给定的黑体强度。
气体的折射率n会受环境温度Tδ以及波长λ影响,具体如下:
(14)
式中:T0为标准温度,n0为气体在标准温度下的折射率,Tδ表示环境温度,η为线胀系数,可由文献[15]查得。
吸收系数a及散射系数σδ可表示为:
(15)
式中:kλ为光谱减弱系数,βλ为散射衰减系数,ρ为气体密度。
对散射角为θ的散射相函数定义为Φ(θ),离散坐标法求解散射光强正是利用勒让德多项式展开,对Φ(θ)做近似处理,展开如下:
(16)
式中:Φg是第g阶勒让德函数,cg是第g阶展开项的系数,可表示如下:
(17)
由式(14)可知,要获得精确的散射相函数需要无穷多阶勒让德多项式展开,在实际计算时,由于只在前向周围很窄的区域内存在显著的前向峰,因此,将散射相函数近似表示为前向部分和截断相函数之和,即:
(18)
式中:f为截断因子,代表前向散射所占比例,M为近似的阶数,cg*为第g阶近似展开项系数。
3 数值结果
液体运载火箭从地面发射后,高度不断提升,随海拔变化的主要参数包括环境压强、环境温度以及飞行马赫数。
为研究液体运载火箭底部热环境变化趋势,本文选取8个典型高度的工况进行数值模拟,表1为这8个工况的自由流条件参数,喷管喉部总温为3800 K,总压为18.66 MPa,气体组分包括H2O,CO2,CO,H2以及空气等。
3.1 不同高度下的马赫数场分布
由图3可知,在5 km~25 km高度,喷管尾焰中马赫波系结构较为明显,特别是在5 km和10 km 时,燃气流场中可见多个喷流波节。由于发动机总压远大于外部环境压强,因此燃气在喷管出口附近形成桶形压缩波,在马赫数云图中可观察到清晰的尾焰喷流核心区、发展段以及射流边界。

表1 自由流条件参数Table 1 Parametric free stream conditions

图3 不同高度下的马赫数云图Fig.3 Contour of Mach number at different altitudes
随着高度逐渐爬升,大气环境压强降低,喷流对外界环境的扰动区域变大,喷流马赫数峰值增大,喷流波节数减少,桶形激波与喷管轴线的交点坐标向下游移动。在35 km~40 km,喷流膨胀半径及膨胀距离剧增,桶形激波与喷管轴线不相交。
燃气在拉瓦尔喷管中处于超临界工作状态,在扩张段形成超声速膨胀波并进一步加速,该膨胀波在喷管尾部由于受到大气压缩作用呈桶形,在喷流激波和喷流边界下游与喷管轴线相交。随着高度上升,环境压强和温度呈下降趋势,外部伴随气流对喷流的压缩作用逐渐减弱,喷流的膨胀程度继续加强,这与图3情况一致。
3.2 不同高度下的底部温度场分布
选取4个典型工况的底部温度场进行对比展示,图4为10 km,20 km,30 km和40 km这4个工况的箭体底部及喷管附近温度场等值线分布图。

图4 不同高度下的温度等值线图Fig.4 Contour of temperature at different altitudes
从图4中火箭底部温度等值线的颜色及疏密程度可以看出,随着飞行高度提升,火箭底部温度整体为逐渐上升的趋势。随着海拔增加,喷管尾部喷流膨胀加强,膨胀后的喷流边界与超声速来流相互作用形成剪切层,喷管喷出的高温燃气在剪切层流动作用下回流至火箭底部,形成对流热流,自由来流、发动机喷流激波与箭体底部及喷管壁面构成一个封闭区域,对流热流在封闭的剪切层区域内形成再循环系统,对箭体底部持续进行对流传热,造成底部对流热流值在前期随着海拔上升逐渐升高。但随着海拔继续上升,尾部喷流激波膨胀剧烈,致使所构成的封闭区域减小,回流至箭体底部的高温燃气量减小,这也是后期箭体底部对流热流下降的原因。
3.3 不同高度下的底部对流热流分布
选取4个典型工况的底部热流云图进行对比展示,从图5可以看出,20 km处对流热流大于10 km处及30 km处,而40 km处对流热流值最小。

图5 不同高度下的对流热流云图Fig.5 Contour of convection heatflux at different altitudes
随着海拔增加,环境压力下降,喷流膨胀加强,引起更多回流,火箭底部的对流换热增加,另一方面,海拔升高时,前方来流马赫数(飞行速度)增加,对箭体底部回流的阻滞效果加强,因而减弱了火箭底部的对流加热。在低海拔时,环境压强对对流热流的影响大于来流速度,所以随着海拔提升对流热流表现为增加的趋势;在高海拔地区,环境压强对对流热流的影响小于来流速度,所以随着海拔提升对流热流表现为降低的趋势。
4 数值模拟与飞行试验对比
在对某三级液体运载火箭数值模拟过程中,选择了与热流传感器相同的位置布置两个监测点,通过数值计算得到了监测点的热流参数,图6显示了两个监测点的数值计算总热流值与飞行实际测量总热流值变化曲线,可以看出两者趋势以及数值大小吻合度都较高。总热流出现了两次峰值,分别是72 s 和99 s,对应的正是10 km附近和20 km附近。
图6中显示的计算总热流值可分解为图7中的对流热流和辐射热流。图7表明,72 s附近的总热流峰值主要来源于辐射加热,99 s附近的总热流峰值主要来源于对流加热。对流热流在50~99 s逐渐增加,并在99 s达到最大值,然后在99~133 s逐渐减小,辐射热流在刚开始达到最大值,然后开始降低。

图6 总热流对比Fig.6 Comparison of total heating rate

图7 数值计算的对流热流以及辐射热流Fig.7 Computed convection and radiation heating rate
从图7还能看出,在较低飞行高度时,辐射热流占总热流的比重较大,而在更高的海拔时,辐射热流逐渐减小,对流热流在火箭底部热环境中扮演更加重要的角色。因为液体运载火箭辐射传热介质主要为H2O和CO2,随着飞行高度上升,环境含气量降低,只能由燃气排放的H2O和CO2作为介质进行辐射传热,所以辐射热流逐渐减小,同时,随着海拔升高,火箭燃气喷流转变为高度膨胀,来自喷管附近的高温气体回流至火箭底部,对底部产生对流加热,因而对流热流增加,当海拔继续爬升时,外界来流马赫数增加,来流对回流的阻滞效果加强,削弱了火箭底部的对流换热,致使对流热流下降。
5 结 论
本文对液体运载火箭的高空底部热流问题进行了数值模拟,并与实际飞行数据进行了对比分析,主要得出以下结论:
1)基于合理假设,建立含燃气-空气多组分Navier-Stokes方程、Realizablek-ε两方程模型和热辐射模型的火箭燃气喷流模型,采用高效的二阶TVD格式离散对流通量,离散坐标法求解热辐射方程,中心差分求解黏性引起的耗散项。对液体运载火箭高空底部热流进行数值研究,仿真结果与测试数据吻合良好,校验了本文所采用的数值方法的精度和有效性。
2)本文的三级液体运载火箭底部总热流出现了两次峰值,第一次峰值在10 km附近,主要受到辐射热流影响所致;第二次峰值在20 km附近,主要由对流热流所致。
3)分别对8个典型飞行高度的工况的热流变化规律进行研究,火箭底部的辐射热流在刚起飞阶段达到最大值,然后随着海拔上升逐渐降低,对流热流表现为先上升后下降的趋势,并在20 km附近达到最大值。
4)在分析液体运载火箭底部的热环境时,需要考虑到对流/辐射耦合换热的影响,本文所形成的火箭高空喷流模型和热流数值模拟方法对液体运载火箭底部热防护安全性设计具有一定的参考价值。

