速度信息缺失的平动点轨道交会预设性能控制
郑丹丹,罗建军,殷泽阳,袁建平
(1.西北工业大学航天学院,西安 710072;2.航天飞行动力技术重点实验室,西安 710072)
0 引 言
近年来,随着平动点动力学性质研究的不断深入,平动点轨道展现出巨大的应用前景[1-2]。世界各国已经发射和正在构想多个平动点观测平台和载人空间站,例如ISEE-3[3]、Wind、SOHO、ACE、MAP、Genesis[4-6]。这些大型航天器的费用高昂,如果发生故障就直接废弃则代价过大,因此需要在轨进行交会对接、维护等操作;更为重要的是,由于平动点轨道非常不稳定,在平动点轨道的不稳定流形方向稍加扰动,处于平动点轨道的高速旋转故障航天器便会在较短时间内偏离轨道,到达地球附近并高速进入大气层,将严重威胁近地空间航天器的安全。因此,研究平动点轨道航天器的交会对接,对于平动点轨道附近航天器的拦截、修复、营救是至关重要的,并且平动点空间飞行器维护系统的成功,将带动深空航天器的重复使用,降低航天成本。
由于平动点轨道重要的应用前景,一些学者对平动点轨道的交会问题进行了研究。Jones[7]对圆型限制性三体问题(CRTBP)中的末段交会问题进行了研究。所提出的制导律实际上是一种两冲量转移策略,仅适用于小幅值的Halo轨道和较近距离交会问题。Marinescu等[8-9]研究了燃料最优小推力交会问题,但交会目标是平动点本身,且仅研究了二维情形。Volle[10]采用变脉冲策略研究了Halo轨道间的交会轨迹规划问题,并在扰动情况下考虑了交会时间和参数之间的影响。Yuri[11]利用拟脉冲集方法实现了地月L2Halo轨道的交会。这些平动点轨道交会采用的方法是开环最优控制方法,也没有充分考虑导航误差、其他行星的引力、测量误差、推力约束等因素。由于平动点轨道自身的不稳定性,在交会过程中有必要考虑这些因素对平动点轨道交会的影响。Lian等[12]利用滑模控制理论研究了地月平动点轨道的交会问题;Peng等[13]利用最优线性反馈控制方法研究了平动点之间的小推力交会问题。通过与开环最优控制方法的仿真结果进行对比,证明了闭环反馈控制在平动点轨道交会中的潜在优势。上述工作均是在相对运动全状态已知的情况下开展的。
国际深空互操作标准草案C-2018组合草案文件[14]指出深空航天器交会出现的突发性状况包括光学敏感器出现故障。因此如果测量敏感器出现故障不能提供速度测量信息,如何实现平动点轨道航天器的安全精确交会是值得深入研究的问题。传统方法一般采用数字差分来近似地估计相对位置的导数,从而得到相对速度状态,但是平动点轨道相对运动存在扰动和测量噪声,而差分方法具有放大噪声的特性,难以正确地估计出高精度的相对速度状态。针对近地轨道缺乏相对速度信息的交会问题,He等[15]采用了有限时间收敛的状态观测器对相对速度信息进行观测,并设计控制律实现了近地轨道航天器的自主交会。但是这种微分器,噪声存在于每一层微分方程中,且不能被充分抑制。而平动点轨道航天器对相对速度状态的精度要求比较高。Wang等[16]提出一种三阶积分链微分器(TICD),该微分器不仅能够高精度地估计原系统的未知状态,而且在对不确定项进行逼近的同时还能抑制噪声。本文拟采用TICD对平动点周期轨道相对运动的速度状态进行估计。
低复杂度预设性能控制(LPPC)[17]方法是近年来发展起来的一种现代控制方法,从提高系统性能的角度进行控制器设计,可确保跟踪误差收敛到一个预设的任意小区域内,同时使收敛速度和超调量都满足预设的条件。该控制方法可以针对模型具有强不确定性的情形,且控制器的设计仅依赖系统的状态反馈,不需要进行大量的迭代计算。国内外学者采用该方法对轨迹和姿态跟踪控制问题进行了探索和研究,均取得了良好的效果。Karayiannidis等[18]采用预设性能控制方法研究了机器人关节的位置跟踪问题,文献[19-20]利用LPPC方法研究了高超声速飞行器参考轨迹跟踪问题,殷泽阳等[21]利用LPPC方法研究了非合作航天器的视线跟踪问题。传统的LPPC方法设计稳态变量的约束条件时,需要事先知道初始误差的符号,因此当改变初始值误差时,一旦初始误差的符号发生改变,就需要改变控制参数,实际操作过程繁琐。
考虑到平动点轨道相对运动动力学的强非线性和强不确定性等特点,以及相对速度难以精确测量或传感器故障造成相对速度测量信息缺失的工况,本文结合TICD和LPPC方法,研究无需相对速度测量信息的平动点轨道航天器交会的自主控制问题。①给出CRTBP的动力学模型和平动点附近的相对运动方程,并将其转化成与控制方法相匹配的形式;②利用TICD估计相对运动速度;③根据初始误差的不确定性提出,一种新的预设性能函数,取消了初始误差符号要求已知的限制;④设计输入状态反馈控制器,并利用李雅普诺夫函数证明其稳定性;⑤通过仿真验证本文所提方法的有效性和鲁棒性。
1 动力学模型和约束条件
平动点周期轨道相对运动模型是航天器交会控制的基础,而应用LPPC方法求取控制力需要具有直接反馈形式的模型。本节建立圆型限制性三体问题的平动点周期轨道相对运动模型,并将其转化成非线性仿射直接反馈形式。
1.1 平动点轨道相对动力学模型


(1)
其中:
(2)
式中:Ωx、Ωy、Ωz分别表示势函数Ω对x、y、z的偏导;Ω为航天器与两主天体P1、P2的距离;r1、r2的表达式分别为:
(3)

(4)
式中:g=-I3×3;f=[F1F2F3]T;具体表达形式为:
(5)

(6)
设aper=[aΔxaΔyaΔz]T∈R3为时变扰动加速度,包含直接、间接引力以及外部干扰等,uC=[uCxuCyuCz]T∈R3为控制输入。本文假设扰动加速度aper是有界未知的,这种假设是合理的:地月系统受太阳引力和太阳光压的量级大约在10-7和10-9[22],即扰动加速度满足不等式
|di|≤Di,i=Δx,Δy,Δz
(7)
1.2 约束条件和参数
本文考虑如下的约束条件:
1)未知扰动的形式。本文考虑的是深空平动点轨道附近的相对运动问题,空间中的外部扰动一般呈现周期性变化,因此可以表示成周期函数的形式[23]
aper=[a1sin(ω1t),a2cos(ω2t),
a3(sin(ω3t)+cos(ω4t))]T
(8)
式中:a1、a2、a3和ω1、ω2、ω3分别是x、y、z方向的扰动幅值及扰动频率。
2)相对导航不确定性。两航天器相对运动过程中需要不断获取相对运动状态,而光学敏感器测量出的相对信息本身存在一定的误差。这种误差直接影响所需控制量的精度。假设相对导航误差满足均值为零的标准正态分布,则带有导航不确定性的追踪航天器的状态可以表示为[23]
(9)

3)推力器故障。由于航天器特殊的运行环境和复杂的结构,推力器很容易出现失效的情况,直接表现形式就是控制加速度的变化,控制加速度的不确定性可以建模为[24]
uC=lCuC+δuC
(10)
式中:lC=[lC1,lC2,lC3]T表示乘性故障,lCi=1,lCi=0,0 当考虑式(8)至(10)的不确定性时,平动点轨道交会轨迹跟踪控制对控制方法的鲁棒性要求比较高。 本节首先给出相对速度信息的估计方法,然后基于TICD估计出的相对速度信息和提出了新的预设性能函数设计航天器自主交会的控制器,在给出控制器设计之前,先给出分析控制器稳定所需的引理。 本文利用TICD来估计两个航天器的相对速度。相对运动方程式(4)的TICD的形式为 (11) (12) 即使存在模型不确定、噪声及外界扰动,TICD仍能有效地估计航天器的相对速度和相对加速度[16],由于高精度的要求,τ取的越小越好,但是过小的τ会使得由式(11)所得到的相对速度很容易会出现很大的超调。如果将由式(11)得到的相对速度用于系统的反馈控制,由于强烈的震荡,会使整个闭环系统发散。因此本文设计如下变摄动参数 (13) 式中:m,1、2为大于零的常数;tmax为最大变化时刻。这样能够保证当0≤t≤tmax时,摄动参数τ的值比较大,从而使得相对运动方程的积分链微分器在初始阶段由于摄动参数比较大,峰值现象可以得到抑制。随着时间的推移,经过初始阶段,τ值变得比较小,从而达到最小值,满足相对运动状态的高精度估计要求。 本文中相对导航的误差满足正态分布函数,因此初始误差的正负号未知,而低复杂度预设性能控制方法要求已知初始误差的符号。为避免频繁调参,本文提出一种新的无需初始误差的预设性能函数。 图1所示的预设性能函数具有两个性质:1)单调递减的正函数;2)当时间趋于无穷时,函数趋于一个任意小的正数。定义如下所示的函数α(t):R+→R+ 图1 预设性能示意图Fig.1 Illustration of prescribed performance (14) 式中:α0、β、ω5>0为预设性能函数的需要设计的参数;ω5是足够小的数;α∞>0为预设性能函数的终值,能够保证状态量Λ最终收敛于稳定域中。 ΓΛ={Λ∈R:|Λ|<α∞} (15) 显然式(14)满足预设性能函数的两条性质,因此可以作为预设性能函数。 针对跟踪误差,利用式(14)定义的预设性能函数,可得不等式约束 -δLα(t)<Λ(t)<δUα(t) (16) 式中:0≤δL,δU≤1是为防止状态量超调而定义的常量,由式(14)看出当ω1→0时α(0)→+∞。 -δLα(0)<Λ(0)<δUα(0) (17) 因此无论初始误差正负都能保证式(17)成立。从而当预设性能函数具有式(14)的形式时,放宽了对初始误差已知的限制。 定义广义状态误差量为 (18) (19) 令δL=[δL1,δL2,δL3]T,δU=[δU1,δU2,δU3]T,由于预设性能函数α(t)=[α1(t),α2(t),α3(t)]T是正函数,式(19)也可写成如下形式 (20) ψi()=ln((i+δLi)/(δUi-i))/2 (21) 令 (22) ψ=[ψ1,ψ2,ψ3]T存在逆映射η(ϑ)=ψ-1(ϑ(t)),其表达形式为 (23) 则转化后状态量的导数如下 λR-1(f-g(d+a))- (24) 式中:χ=diag(α1(t),α2(t),α3(t)),R=diag(r1,r2,r3),其分量ri(i=1,2,3)为ri(ϑi,t)=αi(t)/(∂ηi(ϑi)/∂ϑi)。 针对平动点相对轨道方程式(4),设计预设性能控制器 u=-sgn(G)ζR-1Qϑ/(1-ϑTQϑ) (25) 式中:ζ为可调正常量;Q=diag(Q1,Q2,Q3),其参数应满足下述不等式 (26) 由于g=-I3×3,因此矩阵G=(gT+g)/2为负单位矩阵,因此控制器式(25)可以重新写为 u=ζR-1Qϑ/(1-ϑTQϑ) (27) 下面证明系统的稳定性。 在非空区域[0,tm]内选取如下李雅普诺夫函数 Vϑ=(1/4)(ϑTQϑ)2 (28) 对式(28)的两边求关于时间的导数,得 (29) 将式(24)代入到式(29),得到 (d+a)TgT+uTgT)λR-1Qϑ (30) 而由范数的性质、预设性能函数的定义、平动点相对运动方程以及约束条件可知存在正常数κ1、κ2、κ3、κ4、κ5使得以下不等式成立 (31) 则 (κ1+κ2+κ3+κ4)κ5:κ (32) 将式(25)代入式(30),并结合不等式(32)和g为负单位阵可得 (1-ϑTQϑ))=(ϑTQϑ)(κ-ζλQ(R-1)2 ϑTQϑ/(1-ϑTQϑ))=φ(κ-ζλQ(R-1)2 φ(κ+ρm)((κ/(κ+ρm)-φ)/(1-φ)) (33) 考虑到0<φ/(φ+ρm)<1,因此可以得到 (34) 因此φ(t)在[0,tm]内始终满足不等式0<φ(t)<φm=max(φ(0),κ/(κ+ρm))<1。 进一步可以得到 (35) 结合式(22)以及其单调递增的逆映射ψi可知 即对任意的t∈[0,+∞),李雅普诺夫函数Vϑ=(1/4)(ϑTQϑ)2≤0成立。 以平动点轨道逼近段的交会任务为例对本文所提方法的有效性及鲁棒性进行验证。本文所有仿真利用Matlab R2014a软件,计算机为Windows 7系统,配置Intel(R)Core (TM)2 Duo CPU E7500处理器,主频2.93 GHz,内存2.00 GB,32位操作系统,求解器采用的是固定积分步长的4阶Runge-Kutta方法。值得注意的是仿真过程中,所有的初始条件必须进行无量纲化(具体方法见1.1节)。仿真参数对应的是无量纲化后的动力学模型。 幅值较小的地-月Halo轨道在深空探测任务中是一个非常重要的中转站[25],本文取振幅Az=10000 km的地-月L1Halo轨道为目标航天器所在轨道,其质量参数μ=0.01215。假设追踪航天器和目标航天器的初始相对位置和速度状态分别为[50;0;0] km和[-10;5;6] m/s,最终期望的两航天器相对位置和速度状态为[1;0;0] km及[0;0;0] m/s。外部扰动参数设计为a1=a2=10-7,a3=0,即外部扰动的幅值选取的是太阳引力和太阳光压的最大值,ω1=ω2=π/900。两航天器相对位置导航精度如表1所示[26]。失效推力器所提供的控制加速度的形式如式(36)所示。积分链微分器的设计参数为c1=1;c1=2;c1=3;m=2000;1=0.05;2=8000。控制器设计参数如表2所示。 表1 两航天器相对导航误差Table 1 Relative navigation error of two spacecraft (36) 表2 预设性能函数和控制器参数Table 2 Parameters of prescribed performance 由第2部分的稳定性证明可知,本文所提出的交会控制方法对不确定性和外部干扰具有鲁棒性。下文通过5种工况进行数值仿真验证,工况一(Case 1):假设扰动为零,也不存在导航和制导误差,这是一种理想状态,用来验证本文所提方法的有效性;工况二(Case 2):只考虑扰动;工况三(Case 3):只考虑导航误差;工况四(Case 4):制导不确定性;工况五(Case 5)同时考虑导航误差、扰动以及制导不确定性。后4种工况用来验证本文方法的鲁棒性。 图2和图3分别为两个航天器在三阶积分链微分器-预设性能控制器下的相对位置和相对速度的变化曲线,从图中可以看出,相对位置和相对速度可以分别收敛到期望交会状态的5×10-3km和10-3m/s 邻域内。即表明,可以实现追踪航天器与目标航天器的近程交会任务。相对于理想状态,当推力器存在故障时,系统状态收敛速度比较慢,而扰动和相对导航误差对其收敛速度几乎没有影响。不论哪种不确定性,交会状态的末端误差的量级都为10-3。 图4和图5是5种情况由TICD得到的相对位置和相对速度的估计值。从图中可以看出,即使存在各种不确定性,观测系统的状态仍能以很快的速度高精度地收敛到实际系统的状态,相对速度状态估计值的精度达到10-3m/s,并且由图4可知TICD具有抑制干扰和噪声性能。(注:RV(Real Value)表示实际值;EV(Estimate Value)表示估计值) 图2 相对位置状态变化示意图Fig.2 Relative position response 图6是五种情况追踪航天器所需的控制加速度,在收敛初始阶段,控制加速度会出现一些波动,但波动峰值非常小,都小于3×10-3m/s2,随着控制加速度收敛,对于理想情况(Case 1),控制加速度光滑趋于平稳,对于两航天器相对运动中存在不确定性的情况,其加速度会出现轻微的震荡,但是量级非常小,为10-6m/s2。 300次蒙特-卡洛打靶得到的交会位置和速度误差如表3所示。可以看出,扰动误差对末端相对位置误差影响较大,对末端相对速度误差影响较小,当存在相对导航误差和推力器故障时,相比理想情况相对状态误差都显著增加。 图3 相对速度状态变化示意图Fig.3 Relative velocity response 图4 两航天器相对位置估计图Fig.4 Relative distance estimations 图5 两航天器相对速度估计图Fig.5 Relative velocity estimations 本文针对平动点轨道两航天器交会过程中相对速度测量敏感器发生故障的问题进行了研究。基于三阶积分链微分器设计了仅需相对位置状态的预设性能控制器,并通过理论分析证明了平动点轨道两航天器的相对位置状态和相对速度状态都能在预设性能函数的边界内收敛。最后利用所设计的鲁棒控制器对带有扰动、相对导航误差以及推力器存在故障的情况进行了仿真分析。仿真结果表明,利用TICD可以精确地估计相对速度状态,所提控制方法能够保证系统状态满足实际的预设性能。即使在交会过程中存在各种不确定性,仍然可以实现追踪航天器与目标航天器的安全精确交会,从而验证了本文所提方法具有很强的鲁棒性和高精度的特性。 图6 控制加速度变化图Fig.6 Control accelerations2 基于TICD和LPPC的交会控制策略
2.1 三阶积分链微分器

2.2 预设性能函数的设计

2.3 广义状态量及其转化函数
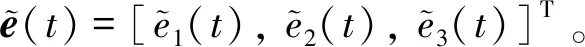




2.4 控制器设计

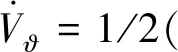





3 数学仿真与结果分析
3.1 仿真初始条件与参数设置


3.2 仿真结果与分析




4 结 论


