中学生成绩的影响因素分析及预测

秦钰娟

（西南大学，重庆 400715）

1 研究目的及背景介绍

1.1 研究目的

通过对葡萄牙两所学校的学生数学成绩分析，了解可能影响学生成绩的因素并建立模型，试图为预测其他具有相似背景学生的成绩提供依据。

1.2 背景介绍

随着社会竞争增大，对学生来说成绩愈发重要，有大量的文章研究过影响学生成绩的因素，主观幸福感对学生数学成绩有积极的影响作用，性格特征对学生不同学科有不同影响，除了这些主观心理因素，生源省份，任课教师，所在学院等客观因素对学生成绩也有影响。本文探讨的指标更客观也更容易推广。

本论文使用的数据是由葡萄牙米尼奥大学的Paulo Cortez 和Alice Silva收集的。表格包含395名葡萄牙中学生的数学成绩以及可能影响学生成绩的30个指标。

2 数据介绍

该数据利用学校报告和问卷调查收集了两所葡萄牙中学学生各方面信息，变量都被整理成为有两个或五个分类的的数字，如表1。

3 模型分析

该文采用方差分析模型。为简明阐述模型，假设自变量有母亲教育程度，学校，更高的教育，恋爱与否。其相应的数学模型为：

其中母亲教育水平的5个程度依次为0,1,2,3,4，以教育水平为4为基准。其他变量以此类推。

方差分析模型的整体显著性，统计学上用以下的方法检验该假设。考虑两个不同的模型：

模型A：G3=母亲教育程度+学校+更高的教育+恋爱与否+随机扰动

模型B：G3=学校+更高的教育+恋爱与否+随机扰动

这两个模型所产生的残差平方和分别记为RSS和RSS，构造如下F-统计量：

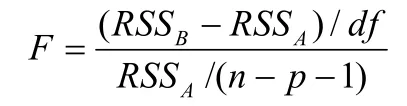
在原假设成立的条件下，该F统计量服从一个自由度为(df,n-p-1)的F分布。若拒绝原假设，则母亲教育程度这个因素是重要的。类似可检验其他因素的显著性。

随机选取数据的80%建立学生第三学年数学成绩G3关于各个因素的回归模型。方差分析结果表明学校，性别等一些因素不显著（假设5%的显著水平），将其剔除后再做方差回归分析结果如表2。

精密量取供试品溶液1 mL，置于100 mL量瓶中，用溶剂稀释至刻度，摇匀，精密量取5 mL稀释液置于100 mL量瓶中，用溶剂稀释至刻度，摇匀，作为灵敏度溶液。

模型的F检验拒绝原假设，说明建立的模型是显著的；调整判决系数为0.15，因为所有的变量中能直接影响G3的很少，但这同时也是我们能将这个模型应用到每个学生的原因，如果有可以很直接影响G3的变量，可能模型的判决系数会很高，可这同时也影响了模型的推广。

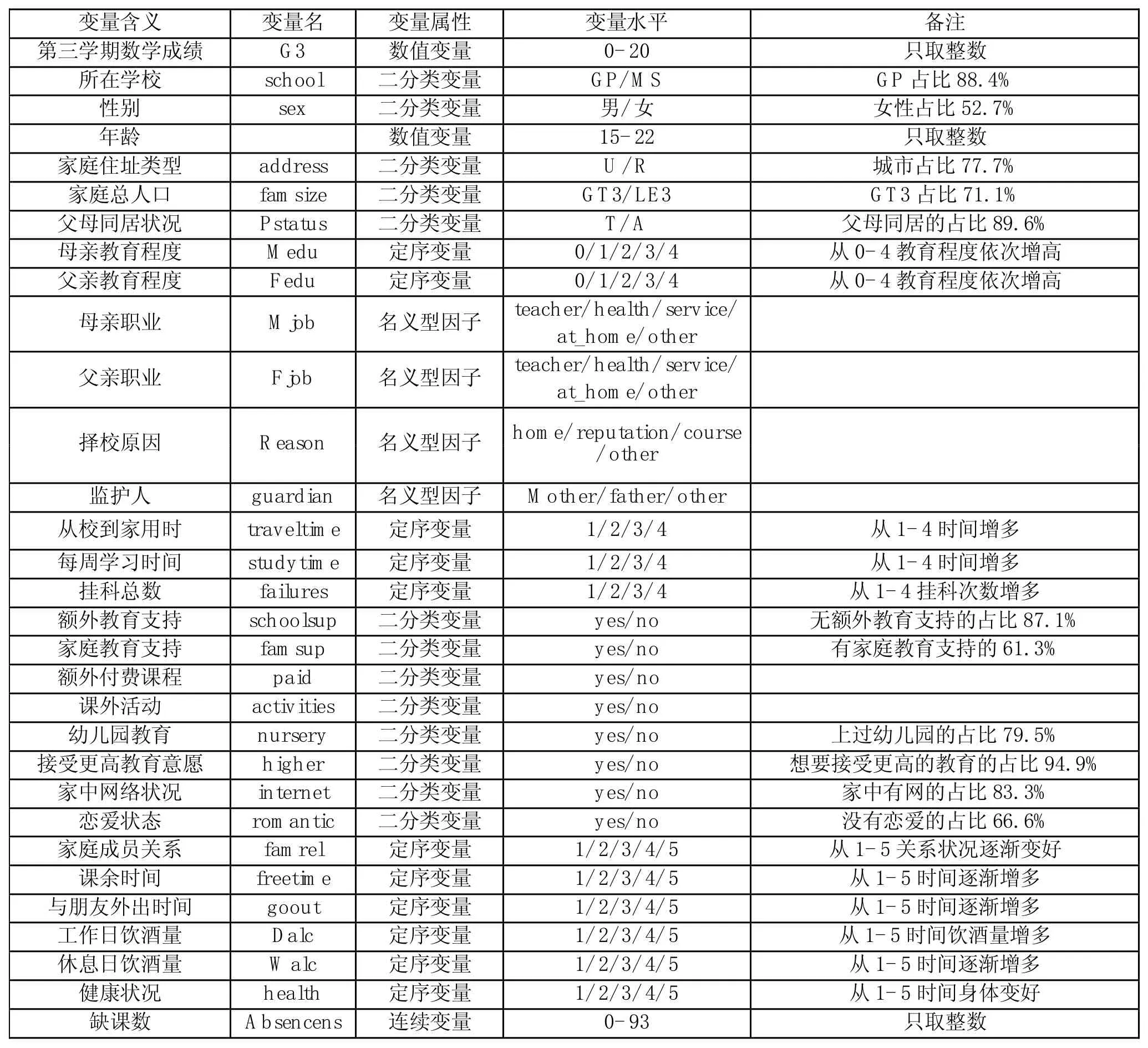
表1 数据介绍

4 对模型中显著因素分析

接下来我们形依次分析各个通过模型检验的变量对G3的影响。

家庭地址在城市和乡村的学生分别有307人和88人，城市学生成绩明显高于农村。

母亲教育程度为0的学生成绩反而要好，这是因为该分类下学生只有3人，样本数量太少不具代表性。随着母亲教育程度的提高，学生的成绩有些许上升的趋势。

每周学习时间小于2小时和2-5小时的学生分别有105人和198人，占总人数的78%。随着学习时间的增加，学生成绩有上升的幅度。

学生挂科数目为0，1，2，3的人数分别为312，50，17和16。随着挂科次数的增加，学生成绩明显呈下降趋势。

随着学生外出时间由非常少到非常多，学生成绩有先上升后下降的趋势。

学生年龄从15到22岁人数依次为82，104，98，82，24，3，1，1。排除样本量小的分类，在前四个年龄中学生成绩随年龄增加稍有下滑。

5 预测评估

选取剩下20%数据应用到模型中并采用相对预测误差预测和检验模型。即

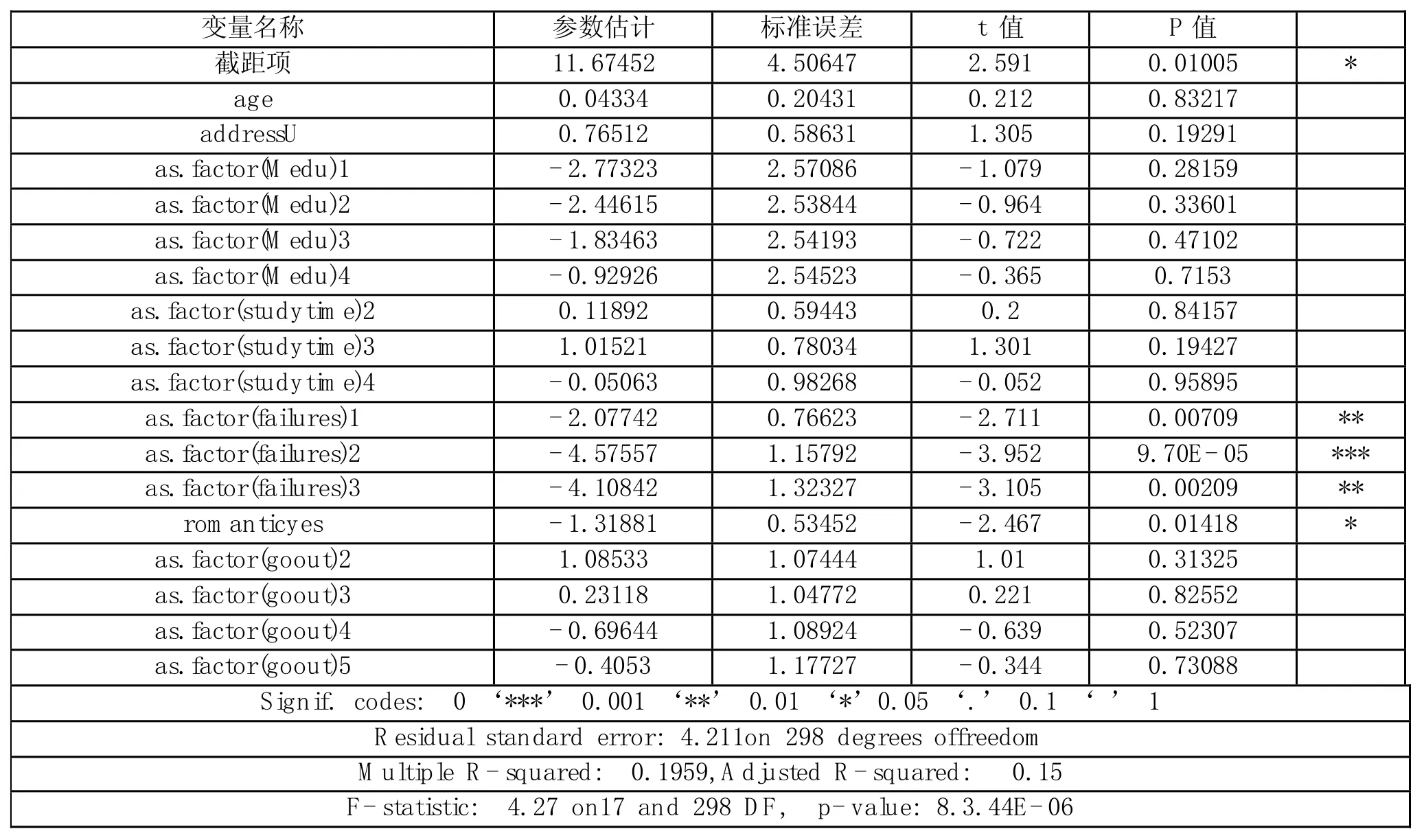
表2 对训练集的第二次方差分析

但是学生成绩预测出来有可能为0，因此在分母上加上0.1。用R求得该相对误差大约为33%。

6 结论及相关建议

由我们建立的统计模型可以得出以下结论：在控制其他因素不变时，可以得到如下结论：

（1）年龄的增加会带来数学成绩的增加，平均年龄增加一岁，数学成绩增加0.04分；

（2）位于城市的学生的数学成绩比农村的平均高出0.77分；

（3）随着母亲教育程度的增加，学生的数学成绩呈上升趋势。这与家庭环境影响学生学习成绩调查研究结论一致，母亲受教育程度是家庭环境的一部分；

（4）学生成绩随着学习时间的增加而增加；

（5）随着挂科次数的增多，学生成绩呈下降趋势；

（6）不谈恋爱的学生比谈恋爱的平均成绩高出1.3分；

（7）适度的外出可以增加学生的成绩。

7 总结讨论

这篇文章探究了学生的数学成绩同学生自身的一些指标的关系。模型的判决系数为15%，相对预测误差为0.33。虽然模型的判决系数并非十分理想，但是鉴于实际情况如：样本量的大小、某些重要的决定性变量未收集等条件等的限制，依旧选择接受该结果。在未来后续的研究中可以从如下方面进行改进：第一，收集一些直接决定学生成绩的因素如：学生的智商水平，学生自身对课程的喜爱程度等。第二，增大样本量收集更多的学生成绩样本。