结合测度整合和AWCBA算法的个人信用评估研究

赵 凯，黄全生，张 玥

(安徽工程大学 数理学院，安徽 芜湖 241000)

近年来，我国信用卡业务快速发展。截至2017年底，我国信用卡累计发行7.9亿张，当年新增1.6亿张，同比增长25.9%，活卡率(180天)达73.1%，未偿信贷余额为5.56万亿元，同比增长了36.8%。个人信用消费行为日趋增多，个人信用评估问题成为信贷行业的研究热点。最初进行的个人信用评估主要采用经验判别法[1]，具有较大的主观性。为了解决这些问题，个人信用评估模型应运而生。最先被用于个人信用评估模型的是统计学和运筹学的方法[2-3]。随着计算机的发展，机器学习方法[4-7]、深度学习方法[8]、数据挖掘方法[9]被不断地运用到个人评估领域。关联规则的概念于1993年被Agrawal[10]等提出，他们同时给出了相应的挖掘算法AIS，但是性能较差。1994年，他们建立了项目集格空间理论，并依据上述两个定理，提出了著名的Apriori算法。在Apriori算法的基础上，学者们不断地对其进行了改进，CBA算法[11]、WCBA算法[12]、CMAR算法[13]等被开发出来。CBA算法作为最早出现的数据挖掘算法之一，是以支持度和置信度作为测度，并视所有属性对规则的重要性一致的算法。WCBA算法是在CBA算法的基础上对属性权重进行了专家打分分析，CMAR算法则是在CBA算法的基础上改进了测度，引入了卡方测度作为新的测度。文中AWCBA算法在属性规则加权上利用支持度、置信度以及卡方测度进行标准化处理并取最大值作为权重，抛弃了传统的专家打分等主观方法；在规则剪枝上采用了利用规则权重自动化剪枝的方法，避免了传统的最小支持度、最小置信度阈值设定不精确的问题；在分类预测上采用了支持度、置信度以及卡方测度的调和均值作为新的测度，解决了单一测度造成的误差影响。在研究中，为了检验所提出算法的准确性，与其他算法进行了比较，最后使用了某商业银行信用卡业务客户的个人信息中的数据来测试所提出的AWCBA算法。

1 AWCBA算法

自1998年出现第一个基于关联的分类算法(CBA)以来,关联分类算法的设计及应用研究一直非常活跃。关联分类算法除了在个人信用评估方面有着广泛的应用，在煤炭安全[14]、文本分类[15]、医学图像数据挖掘[16]的研究中，也起到了显著的效果。在关联分类算法中，人们最关心的问题便是分类结果的准确性，而算法的测度选择则直接影响分类结果。在最开始的研究中，关联分类算法是将支持度和置信度作为测度[17]。当规则的支持度和置信度满足最小阈值时，此规则被收录为强关联规则。

关联分类是数据挖掘中一种新的分类方法，它将关联规则挖掘和分类进行了算法集成，然而，在关联规则的分类算法中，分类器的准确率受到支持度和置信度阈值的影响。以往的关联分类算法都是根据经验人为地设置支持度和置信度的阈值，很难保证分类器总能达到较好的分类效果[18]。另外，在实际应用中，数据库中不同的项目对规则起到不同的重要性[19]。在此基础上进行了改进，提出了AWCBA算法，流程如图1所示。

图1 AWCBA算法流程图

1.1 自适应加权

在传统的挖掘规则中，属性是否重要取决于它在事务集中的计数，并且假定所有属性都具有同等的重要性。但是近年来，研究人员发现，属性是否重要不能单纯依赖于数量方面，事务集中不同的属性对规则起到不同的重要性。因此有必要加强重要属性对规则的影响,同时减弱不重要的属性对规则的影响。

Jaber Alwidian[12]等提出了加权关联规则挖掘，在数据集内，通过一个权重生成算法使用领域知识为项目分配权重，然后将权重输入到算法，将权重应用到项目中，并使用加权支持度生成强关联规则列表。它通过对数据库中的项目赋权来进行规则挖掘，权重用于反映数据库中项的重要性。它的优点是可以在挖掘过程中使用加权支持度发现那些具有高权重的强关联规则。然而大多数数据项不带有预先分配的权重，权重需要受领域内的专家的调整。其中专家可以分配不同的权重，从而生成不同的规则。

对于大多数分类器来说,特征加权一直是分类的瓶颈,特征加权的效果直接影响分类器的分类性能。当数据集有大量项目时，使用领域知识确定所有项目的精确权重可能是不切实际的，并且在不同的类别中，同样的属性可能起到的重要程度也可能是不同的。在这种情况下，文中的AWCBA算法使用了一种新的方法来加权，这种加权方法不再依赖于主观的专家打分加权，同时还可以把不同属性对于不同类别的影响区分开来。

例如，属性a对n类的权重为：

weight(a→n)=

其中，sup(a→n)代表属性a→n的支持度，

式中，δ(a→n)是在类标签为n的所有事物中a的出现频次，T为数据总数。

conf(ra→n)代表属性a→n的置信度，

ka(a→n)代表a→n的卡方测度：

它在权重生成的过程中，通过属性到类的支持度、置信度以及卡方测度的标准化处理，选择3种测度标准化之后的最大正值来生成这种属性对类的权重。这样不需要预先给属性分配权重，而是根据不同属性对类的影响程度不同，自适应地进行加权。

1.2 生成关键项集和重要规则

在传统的关联分类算法中，规则的挖掘分为两个阶段：第一阶段是先从数据样本中利用支持度找出所有的大于最小支持度阈值的项集，叫做频繁项集；第二阶段是在这些频繁项集中挖掘出所有置信度大于最小置信度的规则，叫做强关联规则。例如，在CBA和CMAR算法中都有一个共同的步骤:寻找频繁项集，生成强关联规则。此外，最小支持度、最小置信度在他们的规则挖掘过程中起着关键的作用。在这个过程中研究人员需要根据经验来设置支持度和置信度的阈值，利用阈值进行规则剪枝，支持度和置信度比最小支持度和最小置信度小的规则在剪枝之后会被忽略。例如，如果最小置信度为0.6，最小支持度为0.2，那么如果有一个重要规则的置信度为0.59，则不会生成此规则。采用这种方法很难保证分类器能达到较好的分类效果。

AWCBA算法的理念是取代传统的支持度、置信度构成的关联规则挖掘模型的加权模型，与CBA、CMAR算法相比，AWCB算法的不同之处在于不需要寻找频繁项集，也不需要去从频繁项集中挖掘强关联规则。在第一个阶段，即便在不确定最小支持度、最小置信度阈值的情况下，也可以用数据样本的自身属性去挖掘任何一个对规则产生关键作用的项集，把它称作关键项集。第二阶段，同样利用关键项集中的每一个子集的自身属性来挖掘对类标签产生重要作用的规则，称之为重要规则。

对于一个规则来说，它可能包含若干属性，例如规则r:ab→n。传统的CBA算法中，如果sup(ab→n)≥minsup，则此规则放入频繁项集中；如果conf(ab→n)≥minconf，则此规则为强关联规则。在AWCBA算法里，在给属性加权后，对于规则r:ab→n来说，如果它的属性中有任何权重大于0的属性，则此规则纳入关键项集中；如果它的每项属性彼岸准化之后的带权支持度、带权置信度、带权卡方测度的最大值之和大于0，则此规则为重要规则。接下来，给出一个具体的示例,示例1如表1所示。

表1示例1

事务项属性类标签1ace12bd23bc24abcd15ab1事务项属性类标签6bc27ab18abce19abc210ace1

在示例1中，分别按照传统的关联算法和研究中所述AWCBA算法进行了规则剪枝，其中的强关联规则和重要规则对比如表2所示。

表2 强关联规则与重要规则对照

从示例中可以看出，关键项集不会遗漏任何一个包含关键信息的非频繁项集，重要规则包含的重要信息远大于强关联规则。在如今的信用评估领域，信用良好的客户市场已经趋于稳定，面对大量信用中等的客户，如何从中挖掘属于我们的客户，AWCBA算法中的关键项集与重要规则能产生非凡的影响。

1.3 AWCBA算法

算法分为2个部分，分别是：寻找规则和预测。

算法1：寻找规则

步骤1：输入训练数据，在训练数据中，设置S，令S为空集；

步骤2：令k=1，Sk为每个项目k生成的候选集，r为Sk的子集；

步骤3：对训练数据中的r计算支持度、置信度、卡方测度，进行标准化处理，取三者最大值作为权重，若最大值大于0，则将r加入S′；若最大值小于0，则对规则剪枝；

步骤4：输出S′。

算法2：预测

步骤1：输入测试数据；

步骤2：用S′中的规则对测试数据进行测试，根据类值分组；

步骤3：计算每组的HM值之和；

步骤4：比较两组的HM之和，取较大的一组的类值对数据进行归类。

2 测度整合

在传统算法的预测阶段，对于任何给定的实例，首先检查规则集中的强关联规则。但是，使用支持度和置信度作为度量，支持度和置信度的值都倾向于支持度较大的规则。而使用卡方测度作为度量，卡方测度的值又倾向于支持度较小的规则[20]。尹辉[19]等为了解决此问题，提出了改进的CMAR算法，引入了带权卡方测度作为新的测度。这种测度将支持度和置信度相结合，构造统一度量。Jaber Alwidian[12]等也尝试了结合支持度和置信度的调和均值作为统一度量。所研究AWCBA算法在此基础上将支持度、置信度和卡方测度进行测度整合，构建了整合支持度、置信度和卡方测度的调和均值(即HM)来作为统一的度量。其中，HM值的计算如下：

下面针对示例1比较了各种测度的预测准确度。在示例1中剪枝之后的关键项集中规则的各种测度属性如表3所示。

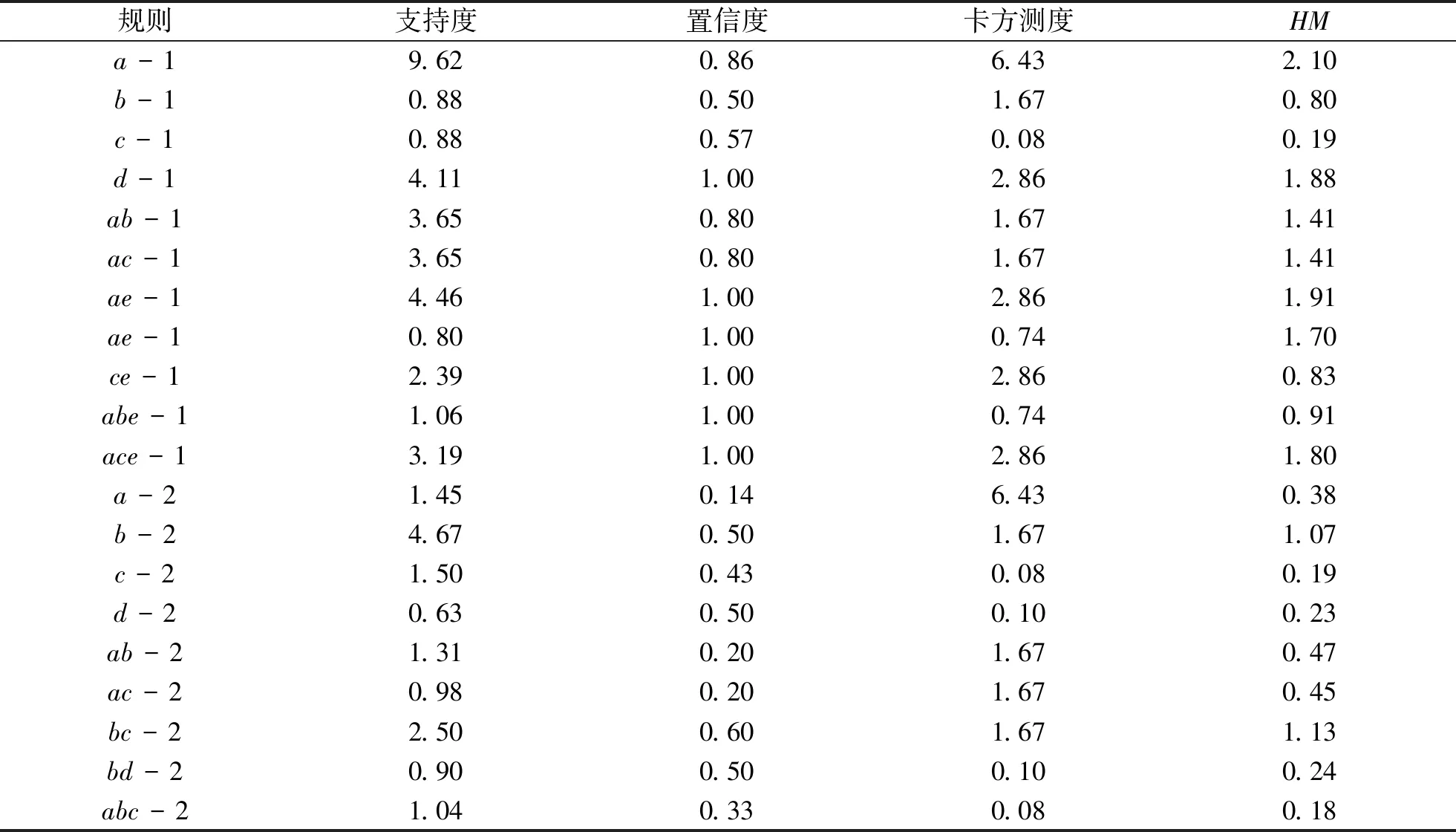
表3 重要规则的支持度、置信度、卡方测度以及HM值

分别选择支持度、置信度、卡方测度以及HM值作为预测测度，预测结果如表4所示。

表4 示例1的4种测度预测准确度

从上面的例子可以看出，构造的统一度量HM值作为预测测度效果优于使用支持度、置信度以及卡方测度的效果。

3 实验

3.1 数据预处理

数据来源于某商业银行的客户信息,总共有1 000条客户记录，每条记录有21个属性项,首先对其进行概化处理，如表5所示。

表5 数据的21项属性以及概化处理结果

3.2 实验结果

实验是在Matlab 2016a上实现的，结果如图2所示。图2中采用了随机抽样的方法，分别抽取10次，每次递增总样本的10%作为训练样本。用4种算法对其进行了实验。从图2中可以看出,AWCBA算法在对某商业银行的客户信用信息数据集上的实验中获得了比CMAR算法、WCBA算法和CBA算法更高的预测准确率。随着测试样本取样数量的递增， AWCBA算法的预测准确率也在提升，并且它的准确率相较于其他3种算法随折变化的波动相对平稳。

采用5次交叉验证的方法对4种算法的预测准确率的实验结果如表6所示。由表6可知， AWCBA算法5次交叉验证的预测准确率均值最高，高达73.25%，WCBA算法的平均准确率次之，而CMAR算法和CBA算法的平均准确度比较低，其中CBA算法的平均准确度才66.32%；并且AWCBA算法的标准差也是这4种算法中最小的，CMAR算法和CBA算法的标准差甚至高达8.72%和8.89%。从这些数据中不难发现，给属性加权了的算法不管是准确率还是稳定性都会有明显的提升。其中AWCBA算法不但是分类效果最好的，而且是稳定性最高的。这说明自适应加权起到了显著的效果。

表65次交叉验证准确率

算法名称均值标准差AWCBA73.253.75CMAR68.688.72算法名称均值标准差WCBA70.525.48CBA66.328.89

至于测度对分类效果的影响，对数据分别随机抽样25%、50%、75%作为测试样本，在AWCBA算法剪枝之后用不同测度(即支持度、置信度、卡方测度、HM值)对它们进行了实验，结果如图3所示。从图3中可以看出，进行过测度整合之后的HM值的预测效果要比其他3种测度好得多。而且随着随机抽样数据的增多，测度预测准确率也越来越高。而其他的测度在面临大量数据时，效果显然比我们的测度要差。所以说，进行测度整合也是提高分类准确度的有效手段。

图2 4种算法实验结果图3 AWCBA算法中4种测度抽样准确度

从上面的3个实验可以得出，不管是测度整合还是属性加权，都可以提升算法的分类正确率。在规则的剪枝过程中，关键项集和重要规则随着数据量的增多，所包含的信息也越来越完善。相比于频繁项集和强关联规则，关键项集和重要规则具有稳定、高效、全面的特点。而且，关键项集和重要规则的筛选方法也至关重要。所以说，对属性进行加权的方法是否先进、对测度进行整合的方法是否科学，也是影响个人信用评估准确率的重要因素。

4 结论

研究提出了一种新的基于AWCBA算法的个人信用评估模型，通过对规则的支持度、置信度以及卡方测度的标准化处理，取规则的3种测度标准化之后的最大正值来生成新的规则权重，剪枝掉标准化处理之后的3种测度最大值仍为负值的规则，并且构建了整合支持度、置信度和卡方测度的调和均值(即HM)来作为统一的度量。在实际应用中，模型不需要主观的加权和人为的设置最小阈值就可以获得满意的分类结果。通过实际数据实验，获得了良好的分类结果，同时证明了AWCBA算法在信用评分系统中具有良好的性能。因此，基于AWCBA算法的个人信用评估模型确实可以帮助银行或贷款人做出正确的决策。当然，研究中的AWCBA算法还有着广阔的提升空间，学习更先进的理论知识来完成算法的升级，是接下来需要努力的方向。