一类无重置条件的机械臂加速抑制初态误差迭代学习控制方法

柴媛媛， 孙中波， 杨宏韬， 李 岩， 刘克平

(长春工业大学 电气与电子工程学院， 吉林 长春 130012)

0 引 言

迭代学习控制(Iterative Learning Control, ILC)最早由Arimoto提出，该控制策略利用前次操作时测得的误差信息和控制输出信号修正当前操作的控制输入，实现输出信号完全跟踪上目标轨迹[1]。因此，迭代学习控制适用于具有重复性质的机械臂系统。为了保证机械臂的收敛性，通常假定每次机械臂运行时的初始状态与期望轨迹的初始状态完全相同[2-4]。但在实际机械臂运行中，很难保证一致的初始值条件。

为了解决不确定性系统的初始值问题，Arimoto[5]分析了当初态误差较小时对迭代学习控制收敛性的影响，指出系统误差可以收敛于某一邻域内。Lee[6]提出了带有初始值修正的ILC算法，并讨论了具有固定初始值偏差的ILC算法在收敛性上优于具有随机初始值偏差的ILC算法。在Lee[6]分析的基础上，孙明轩[7]提出了带有初始值修正的ILC算法，但是该算法需保证初始偏差有界，不能应对具有随机初始值偏差系统的控制问题。对于具有随机初始值偏差的系统控制问题，吕庆[8]提出了带有一段修正区间的ILC算法，该修正区间随着迭代次数增加而减少，有效地抑制了初始值偏差对系统输出的影响。

机械臂系统在重复运行时，每次运行都需重置初始条件，这降低了实验结果的实用性[9-11]。目前，Kwang-HyunPark在传统的D型ILC中加入比例项和误差积分项，用来改善初始误差对控制结果的影响[12]。Chen[13]利用一种初始状态学习方案，结合传统的D型ILC控制律，不需要每次都重置初始条件，得到了跟踪误差的收敛边界，只根据系统的不确定性和外部扰动确定收敛边界，而不依赖初始误差。

文中提出一种无需重置条件下加速抑制随机初态误差的迭代学习控制方法。首先，针对任意初始状态偏差，在时间轴上设计随迭代次数增加而缩短的修正区间。其次，利用控制算法使每次迭代时的初始值无需重置，最后采用二自由度机械臂系统作为仿真验证对象，仿真结果证明文中提出的算法是可行、有效的。

1 问题的提出

考虑n自由度机械臂动力学模型：

(1)

式中：t----时间;

k----迭代学习次数，非负整数;

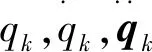
M(qk)----惯量矩阵，M(qk)∈Rn×n;

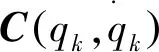
G(qk)----重力矩阵，G(qk)∈Rn;

τk(t)----输入力矩，τk(t)∈Rn。

机械臂动力学模型(1)具有以下性质：

性质1M(qk)正定且有界，满足

0<β1<‖M(qk)‖<β2

0<β1<β2

(2)

性质2M(qk)满足全局Lipschitz连续。

‖M(qk+1)-M(qk)‖≤lm‖qk+1-qk‖

(3)

式中：lm----正数。

性质3G(qk)满足全局Lipschitz连续

‖G(qk+1)-G(qk)‖≤gm‖qk+1-qk‖

(4)

式中:gm----正数。

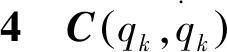
(5)

引理1考虑连续函数f(x,y)，x∈X，X={x∈Rp||x|≤ρi,1≤i≤p},ρi≥0，因此存在L(y)使得

‖f(σ(x1),y)-f(σ(x2),y)‖≤L(y)‖x1-x2‖

∀x1,x2∈Rp，y∈Rq

(6)

式中:‖σ(x1)-σ(x2)‖≤‖x1-x2‖。

证明 利用中值定理，存在z∈Rp，使得

因此

(7)

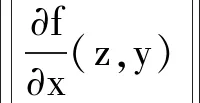
引理2[14]存在z(t)=[z1(t),z2(t),…,zn(t)]∈Rn,t∈[0,T]，使得

(8)

文中做如下基本假设：

假设1G(qk)有界：G(qk)≤lg，式中lg从系统的实际限制获得。

2 迭代学习控制器设计

对于具有随机初始值偏差的机械臂系统，设计迭代学习控制律为

(9)

式中：

(10)

Xk(0)=Dek(0)+xk(0)-xk+1(0)

(11)

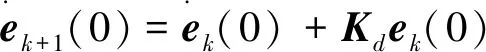
(12)

如果‖In-Kd‖<1,该闭环系统是稳定的，则

(13)

其中，ek=qd-qk，Kd，Kp是对称正定矩阵,D=‖In-Kd‖T，In∈Rn×n为单位矩阵。

证明 为了方便讨论，将使M(qk)≡Mk，G(qk)≡G。

根据式(1)，可得

(14)

使

(15)

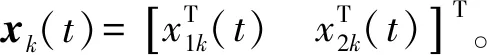
根据式(14)和式(15)，可得

(16)

因此

(17)

其中

对于任意τk(t),t∈[0,T],式(17)的一般解xk(t)如下

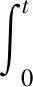
(18)

式中：eA(t-s)----系统的状态转移矩阵。

将式(9)代入式(18)，有

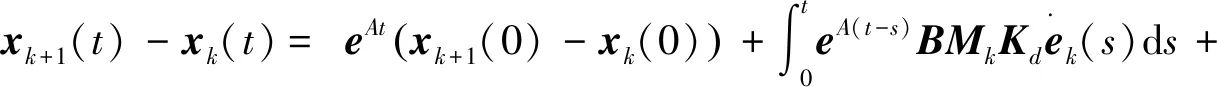
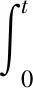
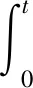
(19)

因此

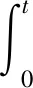
(20)

通过式(9)和式(20)，可得

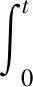
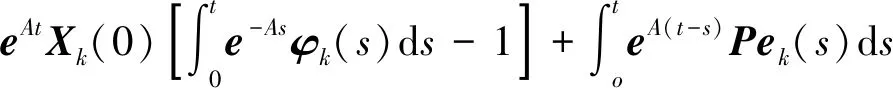
(21)

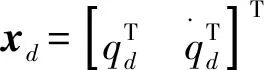
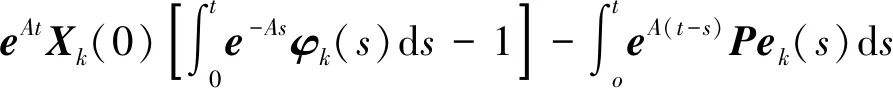
(22)

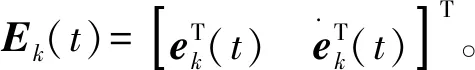
(23)

将式(23)代入式(22)，并在两边同时取范数

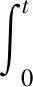
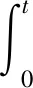
(24)

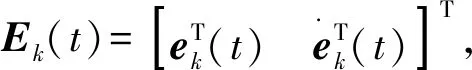
‖ek(t)‖≤‖Ek(t)‖，‖Ek(t)-Dek(s)‖≤‖I2-D‖‖Ek(t)‖

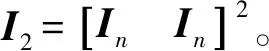
因此

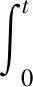
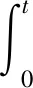
(25)

为了简化等式，令

(26)

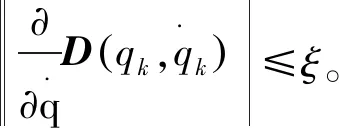
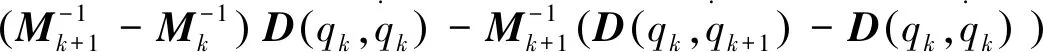
(27)

根据式(26)、式(27)、性质1～性质4、引理1和假设1～假设2，可得

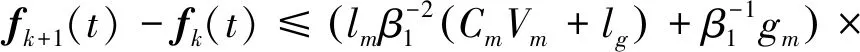
(28)

因此

fk+1(t)-fk(t)≤ω‖Ek+1(t)-Ek(t)‖

(29)

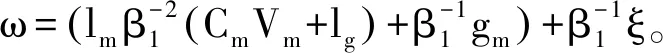
根据式(25)和式(29)可得

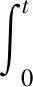
(30)

式中：α=supt·s∈[0,T]‖eA(t-s)‖;

η=‖AD+P‖。

式(30)两边乘e-λt，根据引理2可得

(31)

通过‖I2-D‖≤1，因此‖In-Kd‖<1，存在足够大λ，使得

(32)

因此，根据式(31)可得

‖Ek+1(t)‖λ≤ρ‖=Ek(t)‖λ

(33)

根据式(32)和式(33)可得

(34)

从而

(35)

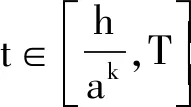
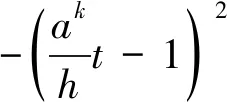
(36)

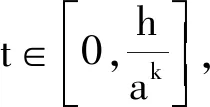
3 仿真结果及分析

为了验证文中控制算法的可行性和有效性，利用Matlab对二自由度机械臂系统轨迹跟踪问题进行仿真实验，机械臂模型如图1所示。

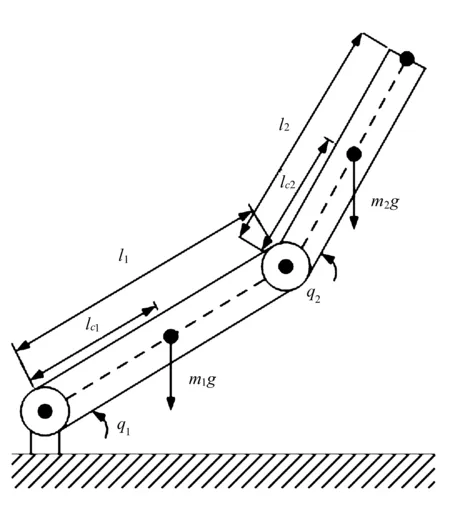
图1 二自由度机械臂系统

Matlab代码是在Matlab R2014a环境下运行实现，CPU为Intel(R)，3.30 GHz，4 GB内存，采用如下动力学模型进行仿真：

c22=0,

g1=m2lc2gsin(q1+q2)+(m1lc1+m2l1)gsin(q1),

g2=m2lc2gsin(q1+q2)。

仿真时各参数实际值为:

m1=2 kg,

m2=2 kg,

l1=0.6 m,

l2=0.6 m,

lc1=0.4,

lc2=0.4,

I1=0.1,

I2=0.1。

仿真参数：

Kd=diag{0.4,0.4}，

Kp=diag{3.5,3.5}，

a=1.003,

h=0.1。

系统的初始转态值由rand函数随机生成。

期望轨迹为：

qd1=sin(4πt)，

qd2=sin(4πt)。

由于定义机械臂每个期望轨迹相同，因此，将机械臂每个输出轨迹与期望轨迹置于一个图内，如图2所示。

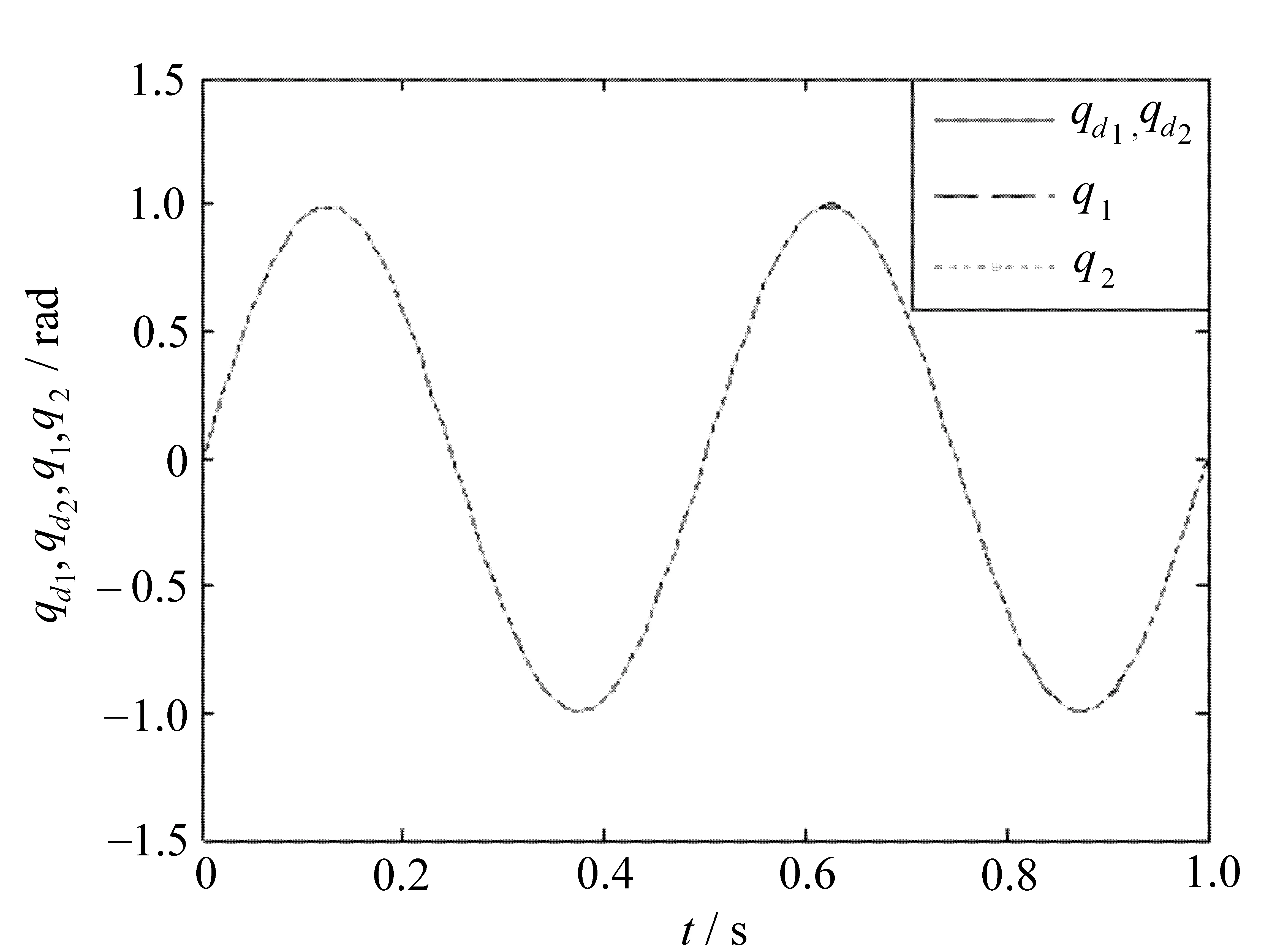
图2 q1，q2跟踪曲线

图中，qd1，qd2为期望轨迹，q1，q2为第20次迭代学习时实时跟踪轨迹。

从图2可以看出，文中所给出的控制律使机械臂的每个输出轨迹在经过20次迭代控制后能有效地跟踪其相应的参考轨迹。

系统跟踪误差随迭代学习次数变化的曲线如图3所示。

e1为机械臂连杆1的跟踪轨迹与期望轨迹之间的跟踪误差，e2为机械臂连杆2的跟踪轨迹与期望轨迹之间的跟踪误差。从图3可以看出，跟踪误差一直在减少，并且开始时误差减少速度较快，在经过10次迭代控制后跟踪误差已经足够小，表明了系统跟踪误差的收敛性。

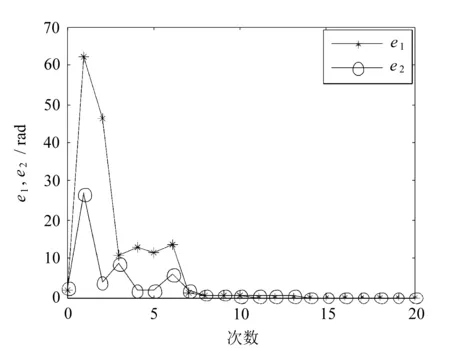
图3 跟踪误差随迭代学习次数变化曲线

为了说明文中提出的迭代学习控制算法对随机初态的加速抑制效果，在相同仿真条件下，二自由度机械臂系统在无加速抑制随机初态的ILC条件下，跟踪误差随迭代次数变化的曲线如图4所示。

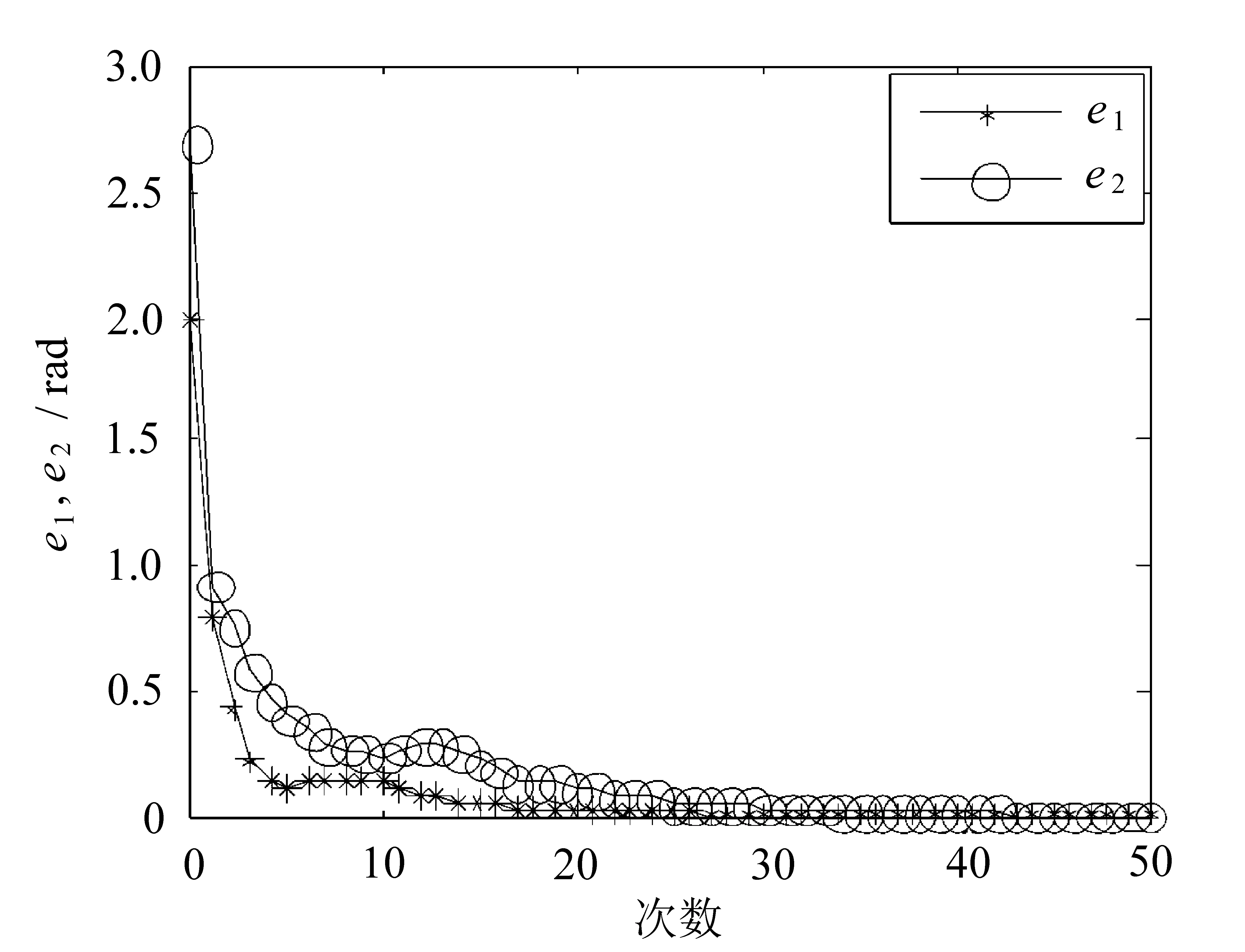
图4 在无加速抑制随机误差的条件下，跟踪误差随迭代学习次数变化的曲线

e1为机械臂连杆1的跟踪轨迹与期望轨迹之间的跟踪误差，e2为机械臂连杆2的跟踪轨迹与期望轨迹之间的跟踪误差。

对比图3和图4可以看出，在文中提出的加速抑制算法下，跟踪误差在第10次左右就可减少到零。而在无加速抑制算法下，跟踪误差在第25次左右减少到零。所以，文中提出的算法对加速抑制随机误差的效果十分明显。

4 结 语

在无需重置条件下研究存在不确定性的机械臂系统，结合PD型迭代学习控制算法提出了一种加速抑制初态误差的迭代学习控制方法。首先，在时间轴上设计了一段随迭代学习次数增加而减少的修正区间。迭代学习控制算法加速了对随机初态误差的抑制，并消除了随机初态误差对机械臂的影响。同时，文中提出的迭代学习控制算法使每次迭代时的初始值无需重置。其次，在λ范数意义下，证明了算法的收敛性。最后，数值结果表明，迭代学习控制算法能够有效加速随机初态误差的抑制。所以，文中提出的算法是可行、有效的。