基于贝叶斯网络的塔里木河流域丰枯遭遇分析*

陈长清1 查显能 严 冬

(1.塔里木河流域干流管理局，新疆 库尔勒 841000；2.华中科技大学水电与数字化工程学院，湖北 武汉 430074)

塔里木河流域位于新疆南部，在天山山脉和昆仑山脉之间，是中国第一大内陆河，主要由阿克苏河、和田河和叶尔羌河汇合而成。由于三源流区的水文特性受气候、下垫面及人类活动的影响，使得三源流年径流量的丰枯变化存在差异性和不确定性，这种不确定性导致了汇入塔里木河干流的年径流量不同丰枯遭遇，直接影响着塔里木河中下游的调水用水的风险。因此对汇入塔里木河干流年径流量的丰枯遭遇的预测需求变得十分迫切。

目前国内外对于贝叶斯网络用于风险分析也有许多研究和尝试，周建方等[1]将多个事件树凝练综合成一个贝叶斯网络，分析了沙河集水库大坝的安全风险；林鹏智等[2]建立了不同因素单独、综合作用下的单库、梯级系统漫坝贝叶斯网络风险分析模型，分析了漫顶风险的主导因素；康玲等[3]对南水北调中线水源区和受水区降雨丰枯遭遇建立贝叶斯网络，通过情景仿真和后验推理功能，模拟了不同丰枯组合对调水的影响；Daniel[4]利用并验证了非参数蒙特卡洛贝叶斯理论在洪水频率分析中的独特优势；H.VAN de Vyver[5]利用贝叶斯网络对降雨极值强度-持续时间频率相关关系进行了分析，并与传统方法进行对比，验证了贝叶斯方法的优越性。本文拟根据贝叶斯网络理论及节点条件概率，建立塔里木河流域年径流量风险遭遇贝叶斯网络结构，分析塔里木河流域三源流的不同年径流组合对干流年径流丰枯遭遇的影响。

1 贝叶斯网络

贝叶斯网络[6](Bayesian Network，BN)，又称信念网络，是由 Judea Pearl 于 1985年首先提出的一种模拟人类推理过程中因果关系的不确定性处理模型。贝叶斯网络是概率、统计与图论组合由有向无环图模型(DAG)和条件概率表(CPTs)组成的概率推理与诊断工具，它将风险管理中的风险因素用网络节点的先验概率表示，用有向边代表节点间的相互关系，由条件概率表达。

若令G=(I,E)表示一个有向无环图(DAG)，其中I代表图形中所有节点的集合，而E代表有向连接线的集合，且令X=xi,i∈I为其有向无环图中的某一节点i所代表的随机变量，若节点X的联合概率可以表示成下式：

(1)

则称X为相对于一有向无环图G的贝叶斯网络，其中，xpa(i)表示节点i之“因”，或称xpa(i)是i的“父节点”(parents)。根据全概率公式，对于任意的随机变量，其联合概率可由局部条件概率分布相乘而得出下式[7]：

p(x1,…,xk)=p(xk|x1,…xk-1)…p(x2|x1)p(x1)

(2)

贝叶斯网络可以用于分析和表达不确定事件和概率性事件。通过建立贝叶斯网络，用节点和连接这些结点的有向边将实际问题抽象化，节点变量可以表达不确定事件间的相互条件概率，有向边可以表示不确定事件间的“子、父节点”关系，由父节点指向子节点。把事件的先验知识通过概率和节点之间的联合概率分布来表示。通过调整节点的概率，实现对后验知识的学习和推理。

2 资料分析

2.1 设计值确定

本文收集了塔里木河流域阿克苏河、叶尔羌河、和田河及塔里木河干流上协合拉、沙里桂兰克、乌鲁瓦提、同古孜洛克、卡群、阿拉尔6个水文站1957—2016年的实测径流资料。其中，阿克苏河天然径流系列资料为库玛拉克河协合拉水文站监测数据和托什干河沙里桂兰克水文站监测数据之和；和田河天然径流采用喀拉喀什河乌鲁瓦提水文站监测数据和玉龙喀什河同古孜洛克水文站监测数据之和；叶尔羌河天然径流采用卡群水文站监测数据；塔里木河干流天然径流采用阿拉尔水文站监测数据。

以皮尔逊三型频率分布曲线得出逐年各频率的设计值。其中丰平枯年等级划分标准见表1。

表1 丰、平、枯等级划分标准

根据表1的丰、平、枯等级划分标准可以确定所求的设计值为X37.5%和X62.5%,这里通过绘制皮尔逊三型曲线得到所需频率的设计值，进而划分丰、平、枯年份，见表2。

表2 各河段年径流量特定频率设计值 单位：亿m3

2.2 丰枯遭遇组合

利用统计方法得到三源流年径流量 27 种丰枯遭遇组合状态，见表3。

表3 源流丰枯27种组合统计结果

3 贝叶斯网络丰枯遭遇风险管理模型

贝叶斯网络结构模型的建立主要有以下3个步骤：ⓐ确定网络结构；ⓑ获得网络参数；ⓒ利用后验知识仿真模拟。

3.1 确定网络结构

贝叶斯网络结构的确定方法有两种[8]：ⓐ通过大量实测数据的结构学习获得；ⓑ由专家知识获得，即根据专家对变量之间的因果依赖关系勾画出网络结构，这种方法对数据的多少要求不高，较为简便。本文采用第二种方法，通过分析各源流区丰枯组合对干流径流量组合的影响，建立丰枯遭遇风险管理模型，其模型结构见图1。

图1 贝叶斯网络结构

图1中是以阿克苏河、和田河和叶尔羌河的年径流量为父节点，以塔里木河的年径流量为子节点，考虑在三源流不同丰平枯组合下，塔里木河的年径流量丰枯遭遇。

3.2 网络参数获取

网络参数即根节点的先验概率和非根节点的条件概率。在建立了网络结构的基础上，结合样本统计数据，计算根节点的先验概率和中间节点的条件概率，输入并完成贝叶斯网络结构。

模型中父节点的先验概率[9]可以通过56年各河段年径流量丰平枯的分布计算获得，子节点的条件概率根据表3中各源流丰平枯27种组合情况下塔里木河的丰平枯概率分布计算获得：

(3)

式中：Ai为27种丰平枯组合中的第i种情况；Bj为塔里木河干流丰平枯情况，j取丰、平和枯3种情况。

将计算出的各种丰枯遭遇概率输入网络结构中得到贝叶斯网络初始模型，见图2。

图2 丰枯遭遇贝叶斯网络

图2中可以看出：阿克苏河与叶尔羌河的年径流量的丰平枯遭遇基本相似，丰水概率为39%，平水23%，枯水38%，丰水概率与枯水概率相差不大，平水概率较小。和田河的丰水概率为32%，平水30%，枯水38%，其中枯水更易发生。相比三源流可见，在枯水发生概率上基本近似，但在丰水发生概率上阿克苏河与叶尔羌河较高。由贝叶斯网络计算出的塔里木河干流年径流量的概率与实际先验知识基本相同，丰枯平水年的分布概率也基本接近。

3.3 仿真模拟

贝叶斯网络不仅可以通过实测数据计算塔里木河干流年径流量的丰枯遭遇概率，即先验概率，还可以通过预测某一节点或多个节点的丰枯遭遇情况，以此为后验信息输入到贝叶斯网络中，通过网络模型的方向推理功能，推测出此节点的变动情况对其他节点的概率影响，为决策者制定应急方案提供数据支撑。考虑塔里木河干流对下游输水的保证，故干流的年径流量的枯水年应值得关注，本文以阿克苏河为枯水，阿克苏河、叶尔羌河均为枯水以及三源流均为枯水这3种情境作为后验信息输入到贝叶斯网络结构中进行仿真研究。

a.情境模拟一：将阿克苏河年径流为枯水情况输入贝叶斯网络结构中得到仿真计算结果，见图3。

图3 阿克苏河为枯水贝叶斯网络

对比图2分析可知：当输入阿克苏河年径流为枯水这一后验信息后，塔里木河干流的丰平枯遭遇发生较大变化，其中丰水概率由33.413%降为21.633%，平水概率略微上升，枯水概率由34.930%上升为42.536%。由表2可知阿克苏河的径流是三源流中流量最多的，故阿克苏河为枯水时，对汇聚塔里木河干流流量影响较大，表现为下游径流量明显减小，枯水更易于发生，丰水难于发生。同时，研究表明：在1994—2003年阿克苏河为特丰水时，和田河和叶尔羌河也为偏丰水时段[10]，塔里木河干流流量更易为丰水。

b.情境模拟二：贝叶斯网络对于后验信息输入的节点个数没有限制，以两节点输入为例，将阿克苏河和叶尔羌河年径流为枯水情况输入贝叶斯网络结构中得到仿真计算结果，见图4。

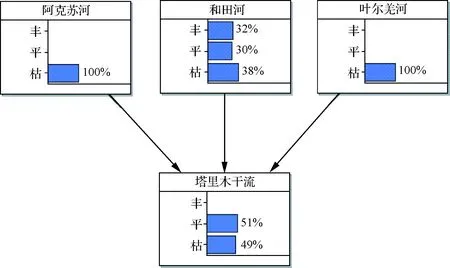
图4 阿克苏河、叶尔羌河为枯水的贝叶斯网络

相比于初始网络模型图2可知:当阿克苏河、叶尔羌河均为枯水时，塔里木河干流的丰枯遭遇发生大幅变化。丰水概率由33.413%下降为0，平水概率由31.657%上升为51%，枯水概率由34.930%上升为49%，并在图4的基础上塔里木河干流的枯水概率更为上升，年径流量减幅明显，可知，阿克苏河和叶尔羌河径流对塔里木河干流径流的丰枯遭遇影响较大，且占主导作用。对于图4的情况，相关部门应采取针对性的应急预案措施。

c.情境模拟三：以三源流均为枯水的后验信息输入贝叶斯网络，得到图5。

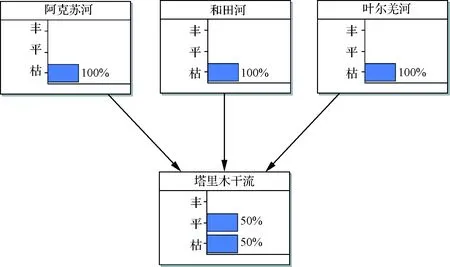
图5 三源流均为枯水的贝叶斯网络

当三源流均为枯水时，相比图4，塔里木河干流平水概率微降，枯水概率微升，这是由于和田河的流量在三源流中为最少，故汇聚在塔里木河干流的权重较小，引起塔里木河干流丰枯遭遇的变化幅度较其他两河源要小。但图5中整体表现的结果为三源流均枯的情况下，导致塔里木河干流的枯水概率较高，为50%，平水概率为50%，无丰水可能性。

4 结 论

本文针对塔里木河流域三源流和干流的不同丰枯遭遇组合情况，建立了基于贝叶斯网络的塔里木河流域三源一干的年径流丰枯遭遇分析模型，并以此得到以下结论：

a.通过先验知识输入模型，塔里木河干流的丰、平、枯水遭遇概率均接近于31%～35%，当输入后验知识阿克苏河为枯时，塔里木河干流的枯水概率上升为42.5%，丰水概率下降。

b.阿克苏河和叶尔羌河年径流量的丰枯对塔里木河干流年径流的影响占主导作用，三河源年径流量对干流影响权重由大到小为：阿克苏河、叶尔羌河、和田河。

c.当后验知识为河源均是枯水时，塔里木河干流枯水概率上升为50%，是水资源调配极其不利的情况，此时相关水利部门应采取相应的应对策略，保证合理可持续的用水调水。

d.该贝叶斯网络模型通过后验知识的不断更新和调整，反映了塔里木河干流丰枯遭遇受三源流的影响规律，进而为流域的水资源合理调配及可持续利用提供科学的决策支持。