液力透平几何参数对压头-流量曲线的影响

杨军虎 马琦航 罗钰铜 姬亚亚 林 彬 李之帆

(1.兰州理工大学能源与动力工程学院， 兰州 730050； 2.甘肃省流体机械及系统重点实验室， 兰州 730050)

0 引言

在化工过程工业中，存在具有高压能量的液体，利用液力透平可回收这部分高压液体的能量。然而在实际化工生产中，其产量是根据要求调节，这时生产的流量也会随之变化，但由于生产工艺的要求其压力一般保持不变。这就要求液力透平的进出口压头随流量的变化较小，即压头-流量曲线比较平坦，以保证生产工艺要求和液力透平机组稳定工作。文献[1-2]研究泵反转作液力透平时两者最优工况下的流量、扬程、压头等外特性参数之间的换算关系，以期指导泵作透平的选型问题。文献[3-4]针对泵反转作透平时，叶轮叶片的进出口角不符合透平工况，提出了液力透平叶轮叶片进出口角的设计方法，设计了专用的液力透平叶轮，数值模拟和试验结果表明，液力透平的效率有了一定提高。文献[5-6]针对叶片包角对液力透平效率的影响进行研究，得出对于每种比转数的液力透平存在一个最佳的叶片包角，蜗壳断面为梯形断面时，液力透平效率最高。文献[7-8]研究了叶轮几何参数对离心泵流量-扬程曲线的影响。

本文基于液力透平的理论分析，研究蜗壳、叶轮叶片几何参数对液力透平压头-流量曲线的影响，以期得到蜗壳叶轮几何参数的影响规律。

1 液力透平的理论分析

1.1 理论压头与流量的关系

液力透平中液体流动满足欧拉方程[9-12]

(1)

式中Hth——液力透平的理论压头

u——叶片圆周速度

cu——叶轮进出口圆周速度分量

下标2表示透平叶轮进口，下标1表示透平叶轮出口。叶轮进出口速度三角形如图1所示。由透平叶轮的进出口速度三角形可得到c2u、c1u，即[13-15]

c2u=c2mcotα2

(2)

c1u=u1-c1mcotβ1

(3)

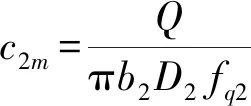
(4)

(5)

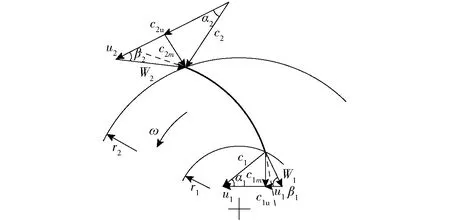
图1 叶轮进出口速度三角形Fig.1 Speed triangle of impeller inlet and outlet

式中c2m、c1m——叶轮进、出口处轴面速度

α2——叶轮进口绝对液流角

β1——叶轮出口相对液流角

Q——透平进口流量

D2、D1——叶轮进、出口边直径

b2、b1——叶轮进、出口边宽度

fq2、fq1——叶轮进、出口排挤系数

排挤系数计算公式为

(6)

式中Z——叶片数

Su——叶片圆周方向厚度

D——叶轮进、出口边直径

叶片圆周速度为

(7)

式中n——叶轮转速，r/min

将式(2)～(7)代入式(1)中可得

(8)

在液力透平中流体在蜗壳及进入叶轮前按等速度矩规律运动[10]，如图2所示，c2u计算公式为

c2ur2=K

(9)

式中K——蜗壳常数r2——叶轮进口半径

(10)

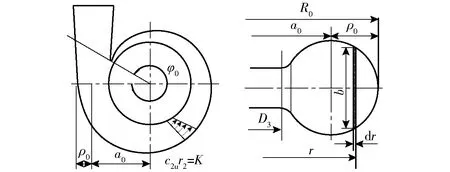
图2 蜗壳内水流的流动Fig.2 Flow of water in volute

蜗壳常数K的计算与蜗壳截面形状有关。离心泵蜗壳断面种类有梯形断面、圆形断面、矩形断面等。不同截面形状下蜗壳常数计算公式为[10]

(11)

式中φ0——蜗壳包角,(°)

r3——蜗壳基圆半径

为了方便，研究时取其蜗壳断面形状为圆形，圆形断面如图2所示。圆形断面的蜗壳宽度b可表示为所在圆半径r的函数关系，则蜗壳常数表示为[11]

(12)

式中a0——蜗壳进口断面与叶轮轴心线的距离

ρ0——蜗壳进口圆断面半径

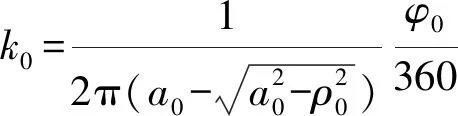
(13)

水流流经蜗壳在叶轮进口处的绝对水流角α2由蜗壳的形状及几何参数决定[9,11]，计算公式为

(14)

将式(4)、(13)代入式(14)则有

(15)

将式(6)、(13)、(15)代入式(8)得到液力透平的理论压头

(16)

式(16)即为液力透平的理论压头随流量的变化关系，可见透平压头随流量增大而增大，且与叶轮、蜗壳的几何参数有关。

1.2 透平压头-流量曲线的影响因素

为了获得平坦的透平压头-流量曲线，将理论压头对流量求导，得出压头-流量曲线斜率为

(17)

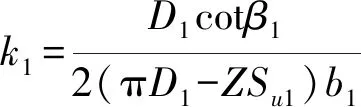
(18)

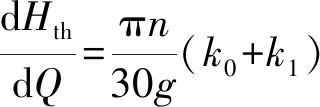
(19)

由式(19)可以看出，透平压头-流量曲线斜率变化主要由式(13)和式(18)中的k0、k1决定。由于透平压头随流量增大而增大，斜率大于零。为了使压头-流量曲线变平坦需减小k0、k1。k0主要由蜗壳参数确定。设理论压头-流量曲线的斜率为hth，即

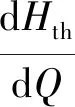
(20)

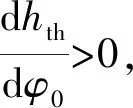
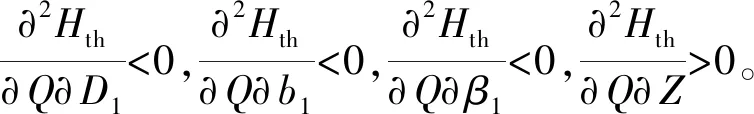
2 透平不同几何参数的研究方案

2.1 研究对象

选用一台比转数为48的单级单吸离心泵反转作为液力透平研究对象，该泵的设计流量Q=65 m3/h、扬程H=94.37 m、转速n=2 950 r/min。叶轮叶片为扭曲叶片，表1为该泵叶轮和蜗壳的几何参数[16-18]。

表1 研究对象主要几何参数Tab.1 Main parameters of study object

根据表1蜗壳和叶轮几何参数，用式(13)、(18)计算得到k0=183.1，k1=10.8，可见蜗壳参数对压头-流量曲线斜率的影响远大于叶轮出口处几何参数。

2.2 数值模拟方案

根据上述分析，在透平叶轮轴面及基本外尺寸和转速不变的情况下设计数值模拟方案。研究时采用控制变量的方法，在原型泵参数基础上，改变上述分析得出的几何参数，在原型泵附近取值，不超过离心泵设计参数取值范围，其他几何参数保持不变。将原型泵作透平命名为方案A；改变蜗壳包角为方案B；改变叶轮出口角为方案C；改变透平叶轮出口边位置和直径为方案D；改变叶片数为方案E。方案B、C、D、E分别取3个参数变量与方案A作对比，研究压头-流量曲线斜率的变化，各方案参数及取值如表2所示。

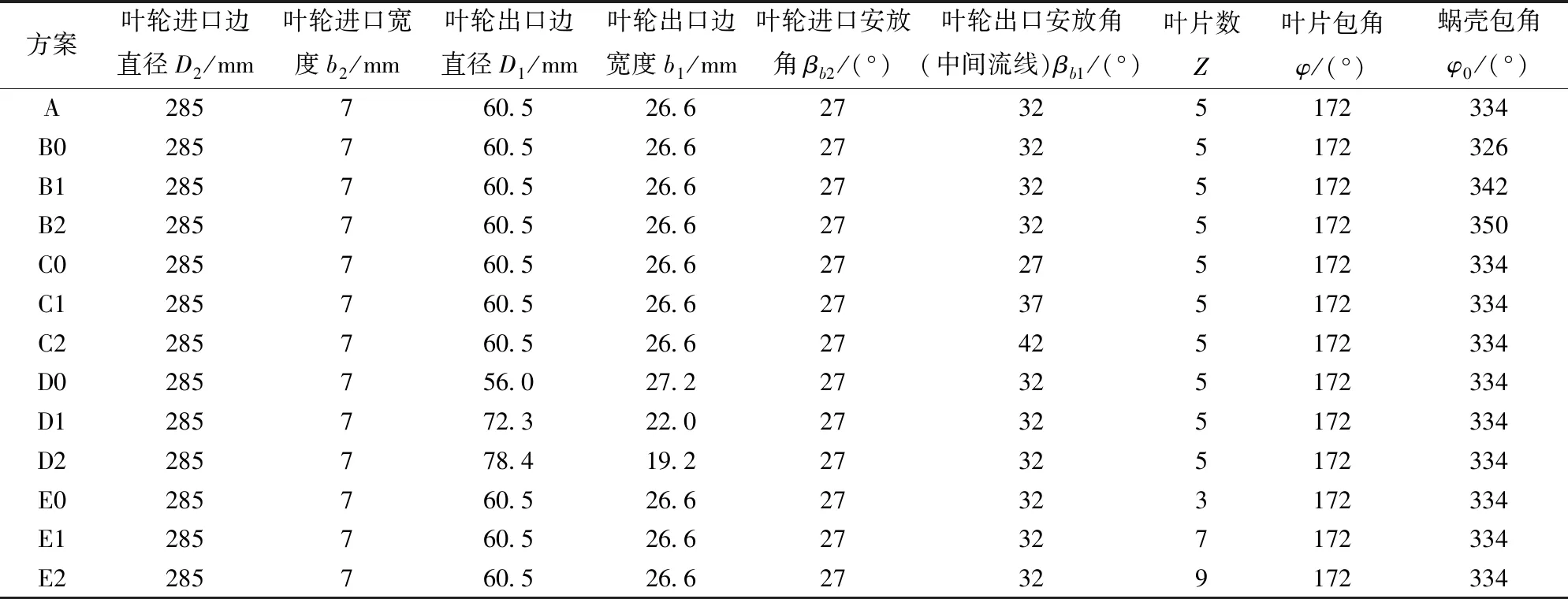
表2 各方案几何参数Tab.2 Geometric parameters of schemes

2.3 计算模型

按表2中几何参数建立了叶轮、蜗壳三维模型。方案A模型叶轮与蜗壳如图3所示。

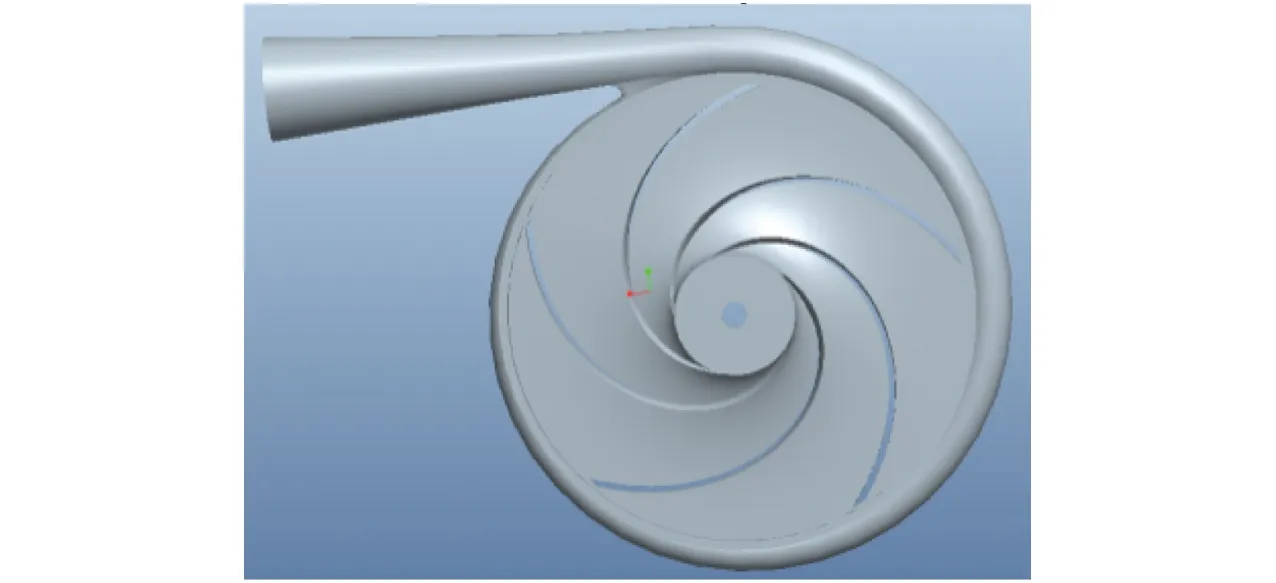
图3 液力透平三维模型Fig.3 3D model of hydraulic turbine

2.4 网格无关性检查

采用四面体进行网格划分并进行网格无关性检测，当网格数大于1.2×106时，求得的效率基本保持不变，则网格数量在1.2×106以上合适。A模型的总网格单元数1 254 342，节点数为212 416。其他模型网格数量与该数量相当。

2.5 边界条件

利用ANSYS-Fluent软件基于压力的求解器，透平进口条件为速度进口，出口设为压力出口，余压设为0.5 MPa。压力与速度的耦合方式为SIMPLE算法，计算收敛标准设为10-5，湍流模型采用RNGk-ε湍流模型，输送介质为常温清水。通过调节进口速度改变透平的运行工况，然后计算得到不同工况下的性能参数。

3 数值模拟试验验证

为了验证数值模拟的准确性，在液力透平试验台上对比转数为48的原型泵反转做透平进行试验，在0.8～2.2倍泵设计工况流量下的8个工况点进行试验[19-20]，试验台如图4所示。

图4 液力透平试验台Fig.4 Hydraulic turbine test bench

透平效率为输出功率与输入功率的比值，即

(21)

其中

Pin=ρgQH

(22)

(23)

式中Pin——透平输入功率

Pout——透平输出功率

M——输出的转矩

ρ——水密度

将试验和数值模拟得到的性能曲线绘出，如图5所示：透平最高效率点为91 m3/h；试验和数值模拟的压头-流量、效率-流量、功率-流量曲线在不同工况点吻合较好，由此可知本文采用数值模拟方法能够对该台泵反转作透平的内部流场进行比较准确的模拟。但试验得出压头略高于数值模拟结果；试验功率与数值模拟功率相差较小；数值模拟的效率略高于试验效率；这是由于数值模拟时忽略了轴承和轴封等引起的摩擦损失。

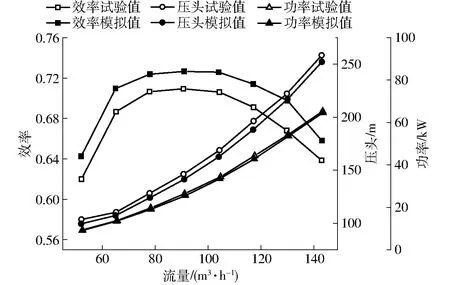
图5 透平性能数值模拟与试验对比Fig.5 Comparison between numerical simulation and test of turbine performance

4 结果与分析

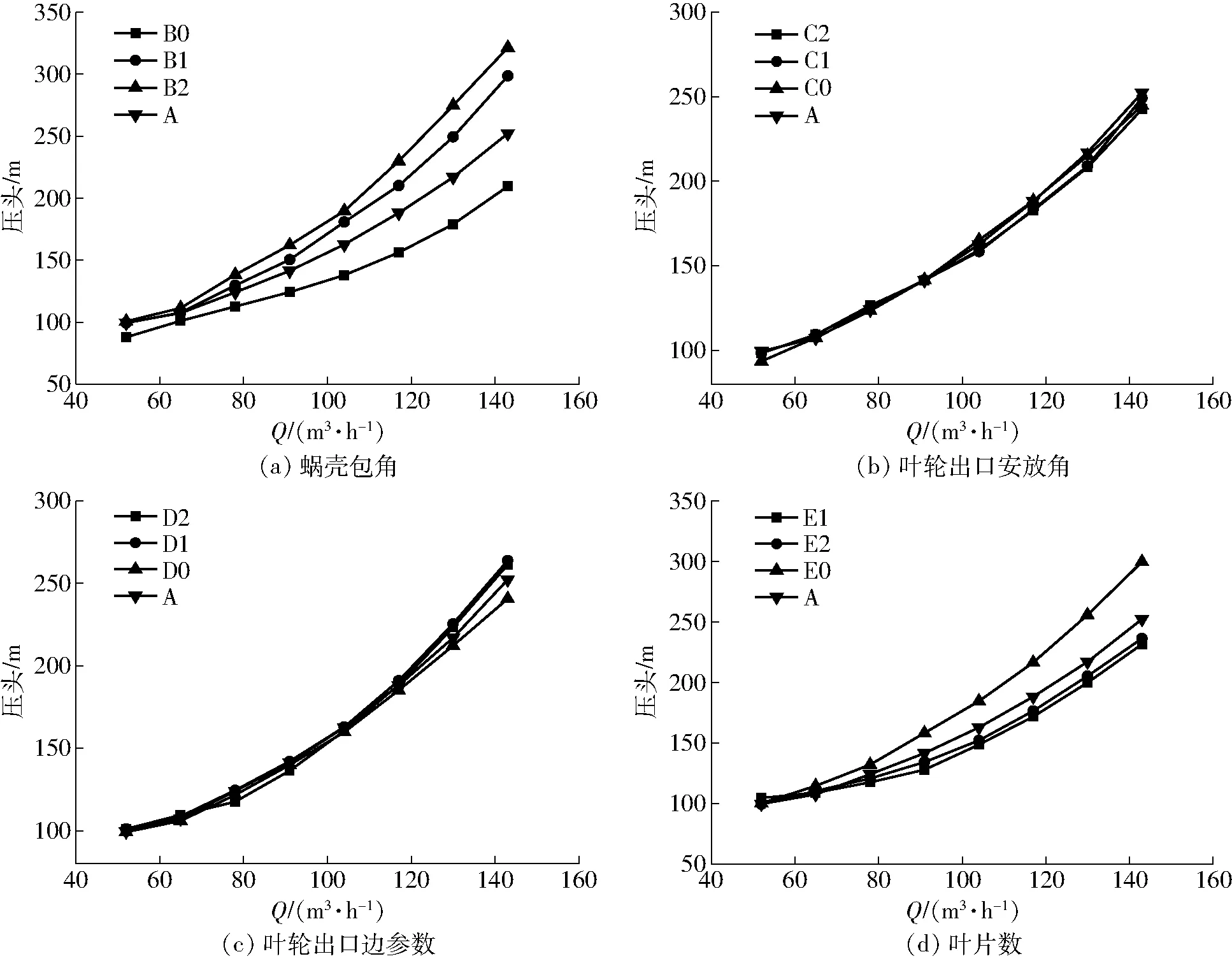
图6 几何参数对透平压头-流量曲线的影响Fig.6 Effects of geometric parameters on head-flow curves of turbine

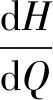
由图6a和各方案斜率看出，压头-流量曲线的斜率随蜗壳包角变化较大,随着蜗壳包角的减小压头-流量曲线变得平缓，这与理论分析结果一致。也说明适当减小液力透平蜗壳包角能够使其压头-流量曲线变得平坦。

由图6b和各方案斜率可以得出，随着透平叶轮出口安放角的增大，压头-流量曲线也变得平缓，但其斜率变化不大，符合理论分析结果。

由图6c和各方案斜率可以看出，在不改变透平叶轮轴面的前提下，透平叶轮出口边前移，这时出口边宽度b1减小，平均直径D1增大，透平的压头-流量曲线在1.4QP处斜率随出口边位置前移先变大后变小，这说明要使透平压头-流量曲线平坦，叶轮出口边有最佳的出口位置。

由图6d和各方案斜率可以看出，透平的压头-流量曲线在1.4QP处的斜率随叶片数增多先变小后变大，这说明对于液力透平，存在最佳叶片数可使压头-流量曲线平坦，对于研究对象，最佳的叶片数是7个。然而理论分析认为叶片数增多会减小透平压头-流量曲线的斜率，这是由于理论分析时没有考虑叶轮的速度滑移现象，也没有考虑叶轮内的损失。

5 结论

(1)在蜗壳内速度矩守恒的前提下推导得到了液力透平理论压头-流量的关系式；分析得出影响压头-流量曲线平坦度的几何参数为蜗壳包角、叶轮出口安放角、叶轮出口边参数和叶片数。

(2)研究结果表明：在一定范围内减小蜗壳包角，增大叶轮出口安放角，会使压头-流量曲线变得平坦；存在最佳叶轮出口边位置和最佳叶片数，可使透平压头-流量曲线更加平坦。其中蜗壳包角对压头-流量曲线斜率的影响显著。