基于两层协调模型的多级扬水灌区供水调配优化

姜 瑶 熊吕阳 姚付启

(1.北京师范大学水科学研究院， 北京 100875； 2.中国农业大学水利与土木工程学院， 北京 100083； 3.长江科学院农业水利研究所， 武汉 430015)

0 引言

灌区水资源优化配置研究始于20世纪60年代初期，研究内容由单一田块、单一作物的灌溉用水优化配置发展到灌区及区域尺度的多层次、多水源联合优化，由单一水量优化发展到考虑水质、生态等环境效益的水资源配置[1-4]。运用的优化技术包括线性规划、非线性规划、动态规划、多目标分解协调法、多目标分解聚合法等[5-8]。随着系统科学的发展，智能优化算法也得到发展，如遗传算法[9]、蚁群算法[10]、粒子群算法[11]、退火算法[12]等。优化模型由单一目标发展为多目标，由传统确定性模型发展为考虑现实诸多不确定性的多种不确定性优化模型[13-15]，并逐渐向数学规划与模拟技术、智能算法、向量优化理论等几种方法的组合模型发展[16-19]。

多级扬水灌区是一个更为复杂的配水系统，不仅涉及到水量在不同系统、不同层次间的分配，还涉及到泵站的运行调度，包括泵站级间流量的配合、水量的分配、扬程优化等。近几十年来，已开展了若干优化模型的构建和开发研究，以优化复杂泵站配水系统运行[7-8,20-21]。然而，模型的数学复杂性、多维特点或对灌溉系统过度简化等限制了诸多模型的应用和推广[20]。因此，建立高效、实用的供水调配优化模型，对多级泵站提水灌溉系统的区域灌溉水资源优化配置具有重要意义。

本文将以宁夏回族自治区典型扬水灌区为例，建立具有二层递阶结构的多级扬水灌区供水调配多目标优化模型。考虑灌区需水及泵站运行情况，将缺水量平方和最小和泵站运行功耗最小作为目标，并考虑不同时段的灌溉配水和泵站运行制度。模型基于大系统分解-协调方法求解，第1层构建单个泵站供水调度优化模型，第2层构建多级泵站供水调配优化模型，各层模型之间通过提水流量和供水量相互协调，以优化和协调多级泵站之间以及单个泵站内作物之间的水量调配。本研究旨在解决复杂多级提水灌溉系统内的供水调配优化问题，以期获得核定水量下不同层次间的水量分配和泵站运行最优方案。

1 系统概述

固海扬水灌区地处宁夏回族自治区中部干旱带(东经105°35′～106°12′，北纬36°11′～37°18′)，气候干旱，水资源短缺，包括固海灌区和固扩灌区两部分，本文研究对象为固扩扬水灌区。灌区南、北长124 km，东、西平均宽2.7 km，由北至南海拔从1 200 m左右增加至1 900 m左右，海拔高差达700 m。灌区内灌溉面积由北向南呈狭长分布，而灌溉水源来自北部黄河水流，由于南北较大的海拔高差，灌区以泵站多级提水灌溉为主。固扩扬水灌区现有主泵站12座，总设计提水流量12.7 m3/s，装机总台数50台，装机总容量9.45万kW，总扬程479.7 m，净扬程428.7 m，1～10泵站装机容量都大于5 000 kW，设计年引水量1.325×108m3。固扩灌区详细组成如表1所示。

在固海多级扬水灌区的供水调配过程中，既存在各级泵站的联合运行，又有站内多台机组的调度，上下级提水泵站之间、本站机组之间都有一定的联系。同时，灌区内又存在诸多蓄水池，用于灌区内的高效灌溉供水。整个灌区的灌溉供水调配取决于整个灌区的来水和需水情况，泵站、蓄水池的运行情况，以及各干渠、支渠和斗渠的水量分配。因此，灌区水量的优化调配不仅是泵站或者渠系本身的优化，还建立在灌区用水计划、渠道水量分配基础上，兼顾泵站运行规则、各级泵站间的合理分配、站内机组优化的整个系统的优化。

2 供水调配优化模型构建

2.1 模型概化

固扩多级供水系统由12级主泵站提水系统和各支渠泵站提水系统及配水系统组成。为简化起见，模型仅考虑主干渠上的多级泵站提水和供水过程，而各分支渠上多级泵站提水仅考虑其取水过程，即每级泵站系统均只有唯一一个上级泵站和下级泵站。因此，固扩多级供水系统可概化为一个由12级泵站系统串联组成的供水系统，每个泵站系统包括泵站提水系统(由进出水结构、水泵机组及泵房组成)和其所控制的灌溉区域(直接从该泵站分水进行灌溉的引水渠道及其控制灌区)。供水系统由首级泵站从黄河干渠取水，进而通过多级提水和供水将水量逐级分配至各泵站供水区内渠系系统和蓄水池，并最终分配至不同作物。其中，根据现场调研，研究区经济作物多数采用滴灌等高效灌溉方式，灌溉水由泵站供水后需进一步经蓄水池沉淀才可灌溉。因此，为简化模型，将粮食作物统一定义为渠系灌溉作物，将经济作物统一定义为高效灌溉作物，以各泵站控制区内两种作物的灌溉配水量分别代表泵站控制区内渠系系统和蓄水池的分配水量，即泵站的输水量和蓄水量(以下简称输蓄水量)。泵站供水量指泵站向其控制区的总分水量，包括渠系系统的输水量和蓄水池的蓄水量。概化的固扩多级供水系统如图1(图中符号定义详见2.2节)所示。

表1 固扩扬水灌区主要灌溉系统组成Tab.1 Detailed information of Gukuo pumping irrigation system

注：a+b表示a台运行机组和b台备用机组。

研究区供水具有多层次且相互联系的供水特点，因此本文建立具有二层递阶结构的大系统分解-协调模型，各层建立多目标非线性优化模型，以考虑供水调配过程中的水量限制和能耗要求。其中，第1层为各泵站系统内的单站供水调度优化模型；第2层为多级泵站系统间供水调配优化模型，模型详细的递阶结构如图2(图中符号定义详见2.2节)所示。

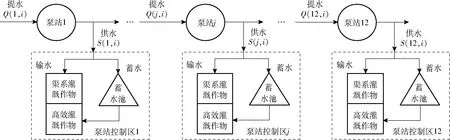
图1 固扩多级供水系统概化图Fig.1 Conceptualized structure diagram of Gukuo multi-pumping irrigation system

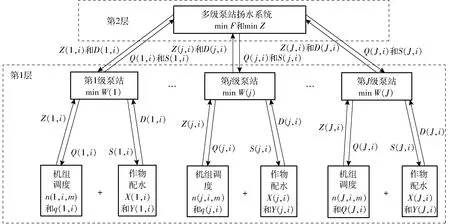
图2 模型递阶结构图Fig.2 Structure diagram of two-level hierarchical model

2.2 模型构建

2.2.1第1层：单站供水调度优化模型

第1层目的是进行泵站控制区内输蓄水量分配优化及泵站内机组运行台数调度优化，模型目标函数为泵站控制区内各作物各时段缺水量平方和最小和泵站运行功耗最小，目标函数方程为

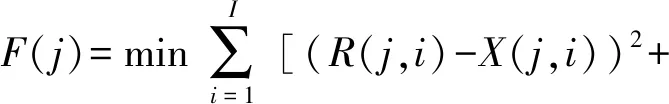
(1)

(2)

式中j——泵站编号

J——各系统内泵站总数

I——运行时段总数

M——泵站内安装机组总数

i——运行时段编号

m——泵站内安装机组编号

Z(j)——第j级泵站运行轴功率，kW

F(j)——第j级泵站控制内作物灌溉缺水量的平方和

R(j,i)——第j级泵站控制区内渠系灌溉作物第i时段总需水量，m3

K(j,i)——第j级泵站控制区内高效灌溉作物第i时段总需水量，m3

X(j,i)——第j级泵站第i时段控制区内渠系灌溉作物配水量，m3

Y(j,i)——第j级泵站第i时段控制区内高效灌溉作物配水量，m3

n(j,i,m)——第j级泵站第i时段第m台机组开机状态，为0～1变量，开机时取1，关机时取0

q(j,m)——第j级泵站第m台机组的提水流量，m3/s

H(j)——第j级泵站扬程，m

η(j,m)——第j级泵站第m台机组在该工况下的效率

由流量-扬程和流量-功率关系曲线确定约束条件为：

(1)灌溉供水量约束

(3)

(4)

(2)可供水量约束

第i时段泵站控制区内总分配水量小于该泵站的供水量，即

X(j,i)+L(j,i)≤S(j,i)

(5)

Y(j,i)≤L(j,i)

(6)

(3)流量约束

开机机组的总流量不小于该泵站的提水流量，即

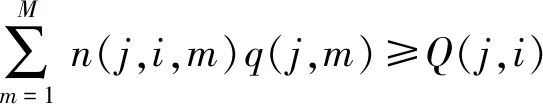
(7)

各机组提水流量不大于其最大提水流量，即

q(j,m)≤qmax(j,m)

(8)

(4)运行台数约束

(9)

(5)功率约束

实际需要的功率不大于机组允许的最大功率，即

Z(j,m)≤Zmax(j,m)

(10)

其中

Z(j,m)=ρgq(j,m)H(j)/η(j,m)

(11)

式中Rmax(j)、Rmin(j)——第j级泵站控制区内渠系灌溉作物最大、最小需水总量，m3

Kmax(j)、Kmin(j)——第j级泵站控制区内高效灌溉作物最大、最小需水总量，m3

L(j,i)——第j级泵站第i时段向蓄水池的分配水量，m3

S(j,i)——第j级泵站第i时段供水量，为协调变量，由第2层模型反馈，m3

Q(j,i)——第j级泵站第i时段提水流量，由第2层模型反馈，m3/s

qmax(j,m)——机组最大提水流量，m3/s

mmax(j)——第j级泵站内最大机组数，为整数

Z(j,m)——泵站内机组运行功率，kW

Zmax(j,m)——机组允许的最大功率，kW

2.2.2第2层：多级泵站供水调配优化模型

第2层目的是优化各级泵站在各时段的供水量和提水流量，目标函数为多级泵站系统总控制区内缺水量的平方和最小和多级泵站系统运行总功耗最小，目标函数方程为

(12)

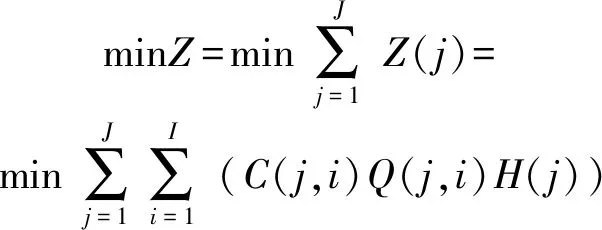
(13)

约束条件为:

(1)水量平衡约束

下级泵站的提水流量与上级泵站提水流量及区间供水流量平衡，即

ω(j)Q(j,i)-Qs(j,i)=Q(j+1,i)

(14)

Qs(j,i)ΔTiη(j)≥S(j,i)

(15)

(2)供水量约束

实际供水量应大于最小需水量，即

(16)

实际供水量应小于由渠道供水能力决定的渠道最大输水量，即

S(j,i)≤Qsmax(j)ΔTi

(17)

系统总供水量应小于系统分配的总水量，即

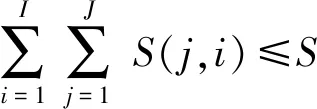
(18)

(3)流量约束

实际提水流量大于最小需水流量，小于由提水能力确定的最大流量，即

Qmin(j)≤Q(j,i)≤Qmax(j)

(19)

第1级泵站提水流量等于整个系统的总提水流量，即

(20)

式中F——整个多级泵站系统控制区内缺水量的平方和

Z——整个多级泵站系统的泵站总功耗，kW

D(j,i)——第j级泵站第i时段控制区内的总需水量，包括渠系灌溉作物需水量和高效灌溉作物需水量，m3

C(j,i)——第j级泵站第i时段的单位提水流量功耗，由第1层模型反馈，kW·m3/s

Qs(j,i)——区间供水流量，包括渠系直接输水流量和蓄水流量，m3/s

Qsmax(j)——由渠道输水能力决定的最大输水流量，m3/s

ΔTi——第i时段持续时间，s

ω(j)——第j级干渠渠道水利用系数

η(j)——第j级泵站系统供水效率

S——系统分配的总水量，m3

Qmin(j)——第j级泵站由最小需水量决定的最小提水流量，m3/s

Qmax(j)——第j级泵站由提水能力决定的最大提水流量，m3/s

2.3 模型求解步骤

(1)各层多目标模型采用基于相对偏差的最小偏差法进行求解，第1层多目标数学模型可描述为

(21)

第2层多目标数学模型描述为

(22)

式中W(j)——转换成单目标后的第1层第j级泵站目标值

W——转换成单目标后的第2层目标值

Fmin(j)、Fmax(j)——第j级泵站控制区允许的最小和最大缺水量平方和

Zmin(j)、Zmax(j)——第j级泵站运行可能的最小和最大轴功率，kW

Fmin、Fmax——整个多级泵站系统控制区内允许的最小和最大缺水量平方和

Zmin、Zmax——整个多级泵站系统可能的最小和最大泵站总功耗，kW

(2)由优化调配模型的第2层给定初始提水流量Q(j,i)和各级泵站向干渠的供水量S(j,i)，其中S(j,i)作为协调变量。

(3)调用第1层单泵站优化模型，在给定流量Q(j,i)和可供水量S(j,i)条件下，通过调节泵站内机组运行台数及其提水流量，对各站流量Q(j,i)在各台机组之间进行优化分配；对各泵站可供水量S(j,i)在灌区不同灌溉作物之间进行分配，求出各级泵站的最优开机方案和配水方案，并确定各级泵站单位提水流量功耗C(j,i)及灌溉需水量D(j,i)。

(4)将第1层得到的各级泵站单位提水流量功耗C(j,i)和灌溉需水量D(j,i)反馈至第2层，再次调用第2层多级泵站优化模型，求解得到第2层各级泵站提水流量Qp(j,i)和各级泵站供水量Sp(j,i)，并确定最优方案下的系统功耗Zp和系统缺水量Fp以及系统目标值Wp(p代表第p次迭代)。

(5)将Qp(j,i)和Sp(j,i)返回第1层，重复步骤(2)～(4)。

(6)反复进行以上过程，直到第2层系统总目标W满足

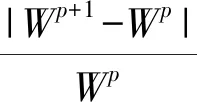
(23)

式中ε——允许误差，取0.001

3 供水调配优化

3.1 模型参数设置

根据收集整理的研究区作物种植结构、作物需水、各级泵站参数等数据，对所构建模型进行了初步验证与应用研究。模型所需数据收集自固海灌区灌溉管理站，包括研究区总核定用水量、作物种植结构、灌溉定额、各级泵站参数(包括总/净扬程、安装机组数及机组运行参数、设计运行方式、设计/最大提水流量、控制灌溉区域及面积等)及近几年各级泵站实际提水量和供水量等。各层模型中需水量根据各泵站控制区内作物种植结构、灌溉面积、灌溉定额及渠系水利用系数计算得到。研究区灌溉提水从4月持续至8月，并在11月进行一次冬灌。因此，模型将灌溉时段划分为6段，每个时段持续时间均设定为30 d。模型中泵站和机组参数及扬程根据收集到的各级泵站实际参数给定，模型中各级泵站最大机组台数根据泵站实际安装机组总数确定，但未考虑各级泵站内备用机组。现状供水方案采用固海灌区2017年实际供水调配结果。优化得到各级泵站各时段提水量、控制区输蓄水量、作物配水量、泵站内机组运行台数调度等方案，并将优化方案与研究区2017年实际供水调配方案进行对比。

3.2 各级泵站间供水调配方案优化结果

在现状供水总量下，各级泵站供水调配优化结果与现状对比情况如表2所示。现状情况下，由于各级泵站同时进行提水和供水，各时段各级泵站系统间泵站供水量分配的不合理往往造成系统较大的缺水量。与现状供水调配情况相比，优化方案对各级泵站供水量进行了整体协调分配，因此优化后的系统缺水量明显减少，各级泵站供水量与其控制区需水量更为接近，总缺水量由现状的5.77×106m3减小为1.30×104m3，各级泵站缺水量(富余量)由现状的-3.22×106～2.47×106m3减小为优化后的-8.30×104～9.50×104m3，缺水量的变化范围显著减小。研究区由于提水级数和扬程较大(12级，净扬程428.7 m)，实际供水中各级泵站间协调难度较大，而通过各级泵站供水量及其系统内机组运行方案调度(机组运行台数及其提水流量的调节)的协调优化，各级泵站提水量均有所增加，同时下级泵站的可供水量增加明显，有效缓解了现状供水中上下级泵站之间的用水调度矛盾，优化后的供水调配方案更为合理。同时，由于提水流量的改变，优化后下级泵站的运行功率虽有所增加，但系统总功率较现状变化较小(表2)。

各级泵站各时段供水量和提水量优化方案分别如表3和图3(图中纵坐标相对提水量为实际提水量(m3)与10 000 m3单位水量的比值)所示。各级泵站各时段的供水量基本与其需水量相近(表3)，这表明通过优化，现状供水总量能较好地满足灌区的需水要求。由于6—8月是大部分作物生长的关键时期，因此随着灌区需水量的增加，各级泵站在该时段的提水量与供水量均显著增加(表3和图3)。同时，下级泵站各时段的提水量和供水量较现状均有所增加，而上级泵站的提水量和供水量受需水量的限制，在一些时段较现状有所减小(表3和图3)。总体上，通过各级泵站各时间段之间的供水优化，多级泵站提水的时空矛盾得到缓解，作物生长关键时期的需水量以及下级泵站的提水量均得到有效满足。

表2 各级泵站供水调配现状与优化结果Tab.2 Present values and optimized results of water supply among multi-stage pumping stations

注：缺水量中负值代表供水量小于需水量，灌区缺水；正值代表供水量大于需水量，灌区供水充足。

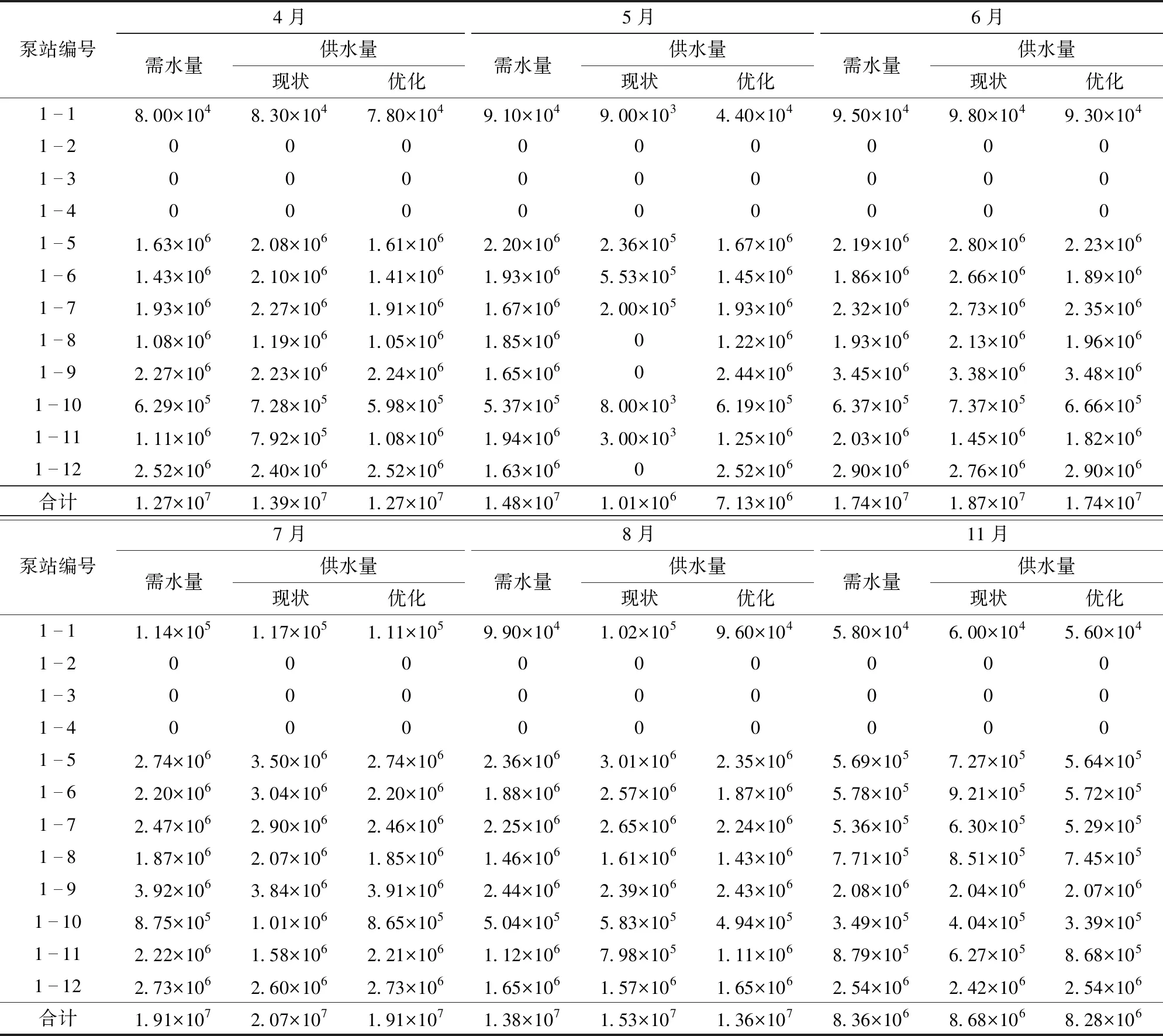
表3 各级泵站各时段供水量优化结果Tab.3 Optimized results of water supply for each pumping station in each period m3

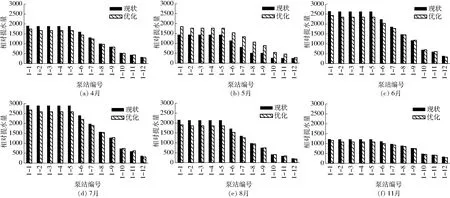
图3 各级泵站各时段提水量现状与优化结果Fig.3 Present values and optimized results of pumping water amount among multi-stage pumping stations in each period

3.3 各级泵站各时段输蓄水量及机组运行台数调度优化结果

基于模型优化，得到的各级泵站控制区内各时段输蓄水量分配方案如图4(图中纵坐标相对水量为实际水量(m3)与10 000 m3单位水量的比值)所示，优化结果给出了各时段各级泵站控制区内的输蓄水量分配方案，为各级泵站的输蓄水量分配决策提供了依据。各时段各级泵站控制区内输蓄水量分配与该泵站控制区内的灌溉面积及作物种植结构密切相关，一般具有较大高效灌溉面积的泵站控制区具有较大供水量及蓄水量。第2至第4级泵站主要负责向下级扬水，其控制区内基本无灌溉面积，因此优化中其配水量为0。第9级和第12级泵站具有较大灌溉面积，其供水量在各级泵站中最大，同时由于第12级泵站的高效灌溉面积较大，因此其各时段蓄水量也相对较大。

各级泵站内机组提水流量及开机组合优化方案如表4所示。各级泵站各时段提水流量为泵站内机组运行的总提水流量，同时优化得到泵站内各机组在各时段的开机状态及流量。在需水高峰的6月和7月，各级泵站的提水流量均为整个灌溉季最大，各级泵站内的开机机组数及机组提水流量也相对较大，最大达到了6台工作机组。在需水量相对较少的4月、5月及11月，各级泵站内机组的开机机组数相对减少，以保证开机机组流量、提高泵站运行效率、减小泵站的运行功耗。

泵站编号4月5月6月7月8月11月提水流量/(m3·s-1)开机组合提水流量/(m3·s-1)开机组合提水流量/(m3·s-1)开机组合提水流量/(m3·s-1)开机组合提水流量/(m3·s-1)开机组合提水流量/(m3·s-1)开机组合116.72#1、#2、#4、#67.13#1～#39.37#1～#410.31#1～#67.38#2～#44.46#2、#4126.42#2～#46.84#2～#49.03#1～#49.97#1～#67.16#1～#34.17#1、#3136.42#1、#3、#46.84#1、#2、#49.03#1～#49.97#1～#57.16#2～#44.17#1、#4146.42#1～#36.84#1、#3、#49.03#1～#49.97#1～#4、#67.16#1～#3、#64.17#3、#4156.42#1～#36.84#2～#59.03#1～#49.97#1#67.16#2～#64.17#1、#4～#6165.55#1、#2、#65.93#2、#3、#67.84#1、#2、#4、#58.49#1～#4、#65.88#2、#4～#63.87#5、#6、#1174.79#1、#2、#5、#65.14#1、#4、#56.84#1、#3～#67.30#1～#44.87#1、#4、#63.56#2、#4183.76#1、#4～#64.10#1、#3、#45.59#1～#3、#5、#65.97#1～#53.66#2、#4、#63.28#2、#6193.20#2、#43.44#3～#54.57#2、#34.98#1、#3、#42.89#2、#32.88#5、#61101.99#3、#5、#62.12#2～#4、#62.70#1、#5、#62.86#1、#3、#61.58#2、#3、#61.76#5、#61111.68#1、#21.79#4、#52.37#4～#62.39#1、#3、#51.32#41.58#11121.11#1、#51.11#1、#3、#41.28#1、#2、#41.20#1、#2、#60.72#2～#41.12#2～#6

注：#代表机组，其后数字代表机组编号。

4 结论

(1)考虑典型多级扬水灌区供水调配过程中不同系统、不同层次间的协调关系，以及水量限制和能耗要求，建立了具有二层递阶结构的大系统分解-协调模型，各层建立多目标非线性优化模型，其中，第1层为单个泵站供水调度优化模型，第2层为多级泵站系统供水调配优化模型。模型基于大系统分解-协调方法求解，各层单独进行规划决策，同时两层之间又通过协调变量(供水量)建立联系，同时兼顾泵站运行规则、各级泵站系统间的水量合理分配、站内机组优化等问题，以解决供水系统中同时存在的高层次的各级系统间供水调配决策和低层次的单级系统内输水量和蓄水量分配优化。

(2)应用所构建模型，开展了宁夏回族自治区典型扬水灌区供水调配优化研究，提出了多级扬水系统内多层次的供水调配优化方案，包括各级泵站各时段提水量及供水量分配、控制区作物配水、站内机组运行台数调度等方案。优化方案与实际供水调配方案对比表明，所构建模型能够高效、合理地解决多级扬水灌区内多层次且相互联系的复杂供水调配优化问题。优化方案较好地缓解了供水系统内各级泵站系统间的供水调度时空矛盾，显著减小了系统缺水量。所构建模型充分考虑了不同层次之间运行规则、水量调配和决策利益的协调，为复杂多级扬水灌区的供水调配优化提供了有效方法。