基于改进势场蚁群算法的移动机器人最优路径规划

张 强 陈兵奎 刘小雍 刘晓宇 杨 航

(1.遵义师范学院工学院， 遵义 563006； 2.重庆大学机械传动国家重点实验室， 重庆 400044)

0 引言

路径规划是移动机器人研究领域的一个重要课题，是机器人完成各种自主移动任务的关键环节之一。根据对环境信息的掌握程度，可将路径规划分为两大类：基于环境信息已知的全局路径规划和基于环境信息未知或局部已知的局部路径规划[1]。目前，用于全局路径规划的算法主要有人工势场法[2-3]、A*算法[4-5]、粒子群算法[6-7]、蚁群算法[8-9]、遗传算法[10]以及神经网络算法[11]等。人工势场算法是基于数学模型的传统方法，其原理简单、计算量小，但应用于复杂环境时，容易陷入局部最优或出现死锁现象。其他智能算法在使用时大都存在计算量大、收敛速度慢、参数不易确定、易于陷入局部最优等问题。近年来又出现了许多改进型算法[12-15]和混合型算法[16-20]。其中，势场蚁群算法就是在综合人工势场算法和蚁群算法各自优点的基础上产生的一种混合算法。

相比蚁群算法，势场蚁群算法具有更好的收敛性和全局寻优特性，部分学者对其进行了相关研究[21-23]。然而，由于人工势场算法本身存在的缺陷以及蚁群算法迭代时存在计算量大等问题，导致势场蚁群算法在迭代过程中耗时长、收敛缓慢以及解的最优性较差。

基于此，本文提出一种改进的势场蚁群算法。该算法先对传统的人工势场算法进行改进，利用障碍物的边界条件替代原有的斥力场函数，使路径可紧贴障碍物的同时避免死锁现象；迭代过程中通过搜寻有效障碍物和路径中间点，逐一进行局部路段的规划，以减少对无效障碍物的冗余计算，从而有效缩减算法的计算量。再以改进人工势场算法的规划结果重构蚁群算法的启发信息，用以避免算法初期由于蚁群盲目搜索导致的收敛速度慢等问题；在迭代过程中利用收敛次数构建负反馈通道，使全局和局部信息素的更新速率可自适应调节，以协调收敛速度与全局搜索能力之间的固有矛盾。

1 基于栅格法的环境建模

栅格法是移动机器人环境建模中一种常用的方法[18,23-25]，其基本原理是利用棋盘的思想将机器人的移动空间离散化为若干个栅格，并根据栅格的可通过性将其分为自由栅格和障碍物栅格。对于障碍物而言，目前主要的栅格化方法有腐蚀法和膨胀法两种[26]，不同算法所得到的障碍物栅格存在较大的差别，如图1所示。

图1 障碍物的栅格化Fig.1 Grid processing of obstacle

设机器人可移动的平面矩形范围为l×h，其中起点为原点(0,0)，目标点为矩形中的对角点(l,h)，取正方形栅格尺寸为a×a，则长宽方向上的栅格数分别为

(1)

式中Nh——宽度方向上的栅格数目

Nl——长度方向上的栅格数目

ceil——向上取整函数

根据每个栅格所在行和列的编号生成相应的坐标(x,y)，取左下角栅格的坐标为(0,0)。由于自由栅格在遍历过程中需要被遍历，而障碍物的栅格在遍历过程中无法被遍历，因此对每个栅格设定一个属性值γ(x,y)，取值如下

(2)

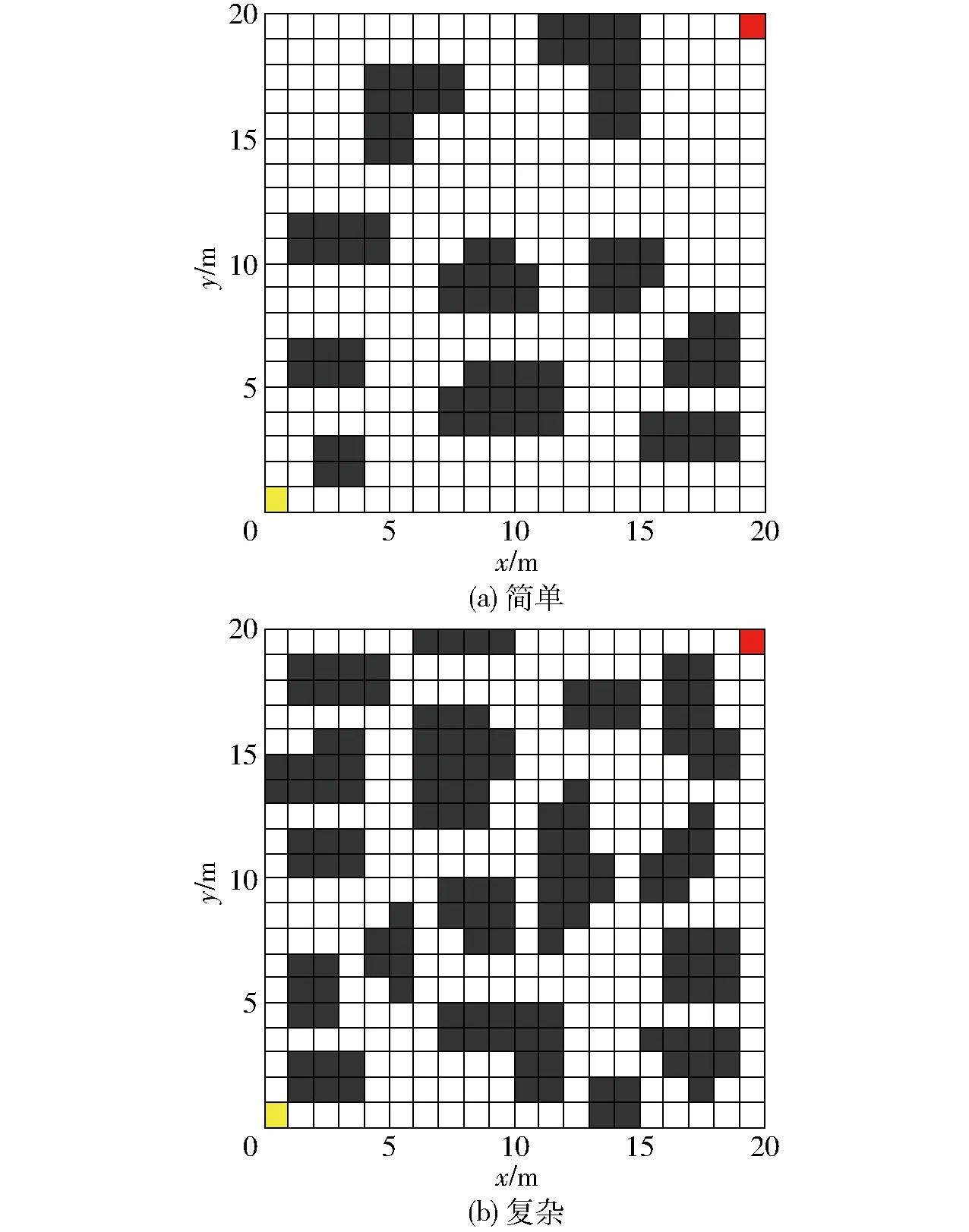
图2 两种仿真示例环境Fig.2 Two example environments for simulation

为考查本文算法对不同环境的适用性，在Matlab中建立如图2所示的两种仿真示例环境，其中右下角栅格代表机器人的起始点，左上角栅格代表目标点。

2 基于改进人工势场算法的局部路径规划

2.1 人工势场算法的基本原理

人工势场算法是由KHATIB和KROGH最早提出来的一种虚拟力法[27]。它的基本思想是在机器人的运动环境中施加一种虚拟的人工力场，其中障碍物对机器人产生斥力，目标点对机器人产生吸引力，机器人在两种力的共同作用下运动。设二维平面内机器人所处的位置为X=[xy]，目标点所处的位置为XM=[xmym]。定义引力势场函数[28]为

(3)

式中kg——引力场的增益系数，为正数

相应的引力FG(X)为引力势场函数的负梯度，计算公式为

(4)

其中

ξ1=‖X-XM‖

式中ξ1——机器人和目标点之间的距离

α1——从机器人所处位置指向目标点的单位向量

由此可见，引力与机器人到目标点的距离呈线性关系。定义各障碍物产生的斥力场函数为

(5)

式中ξ——机器人与障碍物边缘之间的最短距离

ξ0——障碍物所影响的最大范围距离，其值需结合实际环境进行优化得到

k0——斥力场的增益系数，为正数

式(5)表明机器人位于距障碍物边缘ξ0的范围内将受到障碍物斥力的影响，而超出这一范围时机器人将不再受其斥力的作用。相应的斥力F0(X)为斥力场函数的负梯度，计算公式为

(6)

机器人所受的合力F(X)为

F(X)=FG(X)+F0(X)

(7)

传统人工势场算法在进行机器人路径规划和避障时，存在如下问题：

(1) 当所有障碍物产生的斥力之和与引力大小相等，方向相反时，即形成了所谓的死锁现象(Deadlock)[29]，机器人在该点处将无法移动，如图3所示。

(2) 当目标点处于障碍物附近时，由于斥力作用的影响，可能导致目标点不可达的问题。

(3) 当障碍物较多时，计算每个障碍物所产生的斥力，将导致算法的计算效率急剧下降。

(4) 受斥力的影响，机器人无法紧贴障碍物运动，从而导致所规划的避障路径不一定最短，甚至在一些障碍物较为密集的区域出现规划失败的情况。

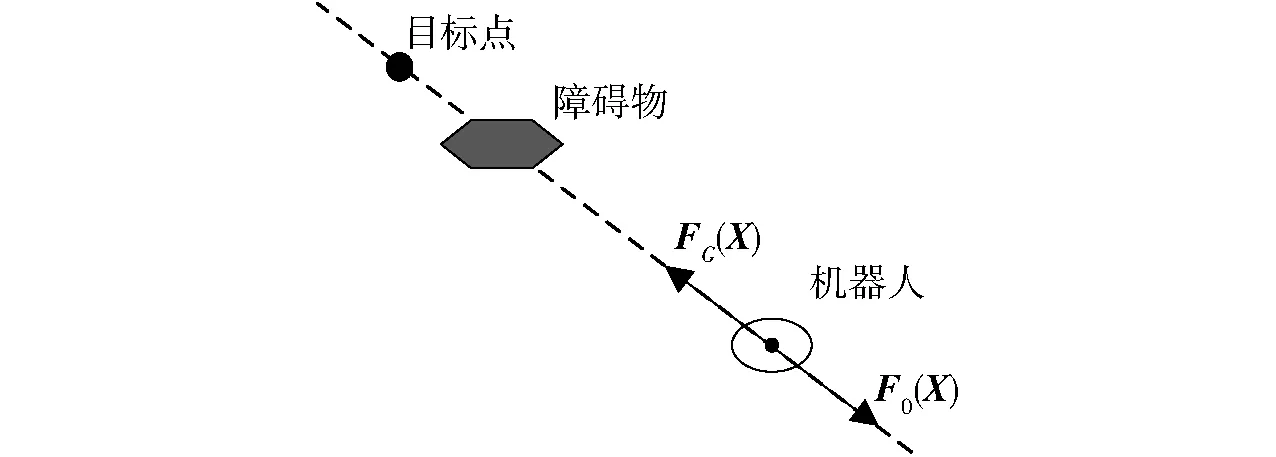
图3 机器人运动过程中的死锁现象Fig.3 Deadlock in process of robot movement

2.2 改进人工势场算法

改进人工势场算法的基本思路是先利用障碍物检测算法识别出有效障碍物及一个路径中间点，再利用终点的引力和各障碍物边界条件进行起点到中间点的局部路径规划，最后将中间点置为新的起点，重复以上过程，直至起点迭代至目标点为止。

2.2.1障碍物检测算法

障碍物检测算法主要用于检测对机器人移动路径有影响的障碍物，称其为有效障碍物，并在其周边搜寻到一个合适的点作为路径中间点。障碍物检测算法的基本思想是：先构建一条从起点到终点的直线，然后从起点处沿直线方向进行搜索，当发现存在障碍物时，将其置为有效，同时计算该障碍物每个边沿点到直线的距离，找出正负方向上的两个极值点，取其绝对值最小的点作为路径中间点。

设机器人的起点为XS=[xsys]，终点为XD=[xdyd]，则栅格环境地图中起点到终点的直线Σl方程定义为

(8)

式中 round——取整函数

设机器人移动的环境范围为{(x,y)|0≤x≤Nh且0≤y≤Nl}，定义栅格到直线Σl的距离为

(9)

式中i、j——栅格的横、纵坐标

K——常数，取较大的正整数

将环境边界栅格到直线的距离定义为较大值，可避免将其选作中间点。由式(9)可知，对于非边界栅格，其到直线Σl的距离可为正数也可为负数，因此对于有效障碍物Ω的边沿栅格，必存在两个点到直线Σl的距离分别为正数的最大值和负数的最小值，设该两栅格坐标分别为Xmax,ω=[xmax,ωymax,ω]、Xmin,ω=[xmin,ωymin,ω]，各自对应的最大距离和最小距离分别为dmax,ω和dmin,ω，则障碍物Ω周边存在的路径中间点坐标Xl,ω=[xl,ωyl,ω]为

(10)

(11)

2.2.2人工势场算法的改进

在栅格地图环境中，规定机器人可进行8邻域的移动[30]，即机器人每次只能移动到相邻的某个栅格内。据此规定机器人在栅格环境中只能受8个方向上的作用力，用3×3的矩阵来存储，并称其为力向矩阵，其中各元素所代表的力方向如图4所示。

传统人工势场算法中，由于障碍物对机器人存在斥力作用，致使机器人无法紧贴障碍物移动，因此本文去掉障碍物对机器人的斥力作用，而引入一个与障碍物有关的边界条件，即机器人在邻近障碍物方向上的受力始终为零。故机器人在各方向上的受力只与终点产生的引力和其所处的外部环境有关，定义机器人在X处的力向矩阵为

(12)

式中Eij——环境约束矩阵

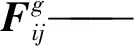
*——卷积运算

环境约束矩阵Eij主要反映机器人周边8邻域栅格的状态，本文取3×3阶的矩阵，各元素定义如下

(13)

(14)

最优分解是指矩阵中各元素满足

(15)

式中m——FG(X)矩阵元素的行代号，m∈{-1,0,1}

n——FG(X)矩阵元素的列代号，n∈{-1,0,1}

αij——X处机器人可移动的方向向量，αij=(m，n)

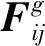
规定机器人进行局部路径规划时总是向受力最大的方向运动，则路径点的迭代公式为

X′=X+λij

(16)

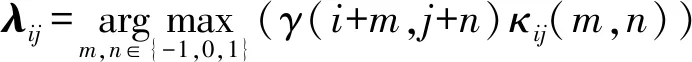
式中λij——X处机器人所受最大引力分量的方向向量

X′——下一路径点的位置向量

2.3 改进人工势场算法的具体步骤

基于改进人工势场算法的局部路径规划步骤如下：

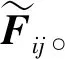
(2)运用障碍物检测算法搜索到有效障碍物及一个中间点，将中间点置为局部路径的终点，重复调用障碍物检测算法进行搜索，直至没有发现新的有效障碍物和新的中间点为止，此时的终点即为第1个有效中间点，并将最后一个有效障碍物的栅格属性数据从ZX复制到ZS中。

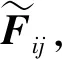
(4)将终点置为新的起点，将目标点置为新的终点，重复步骤(2)和步骤(3)，直至起点变为目标点为止，则路径规划结束，所得的各段局部最优路径即构成机器人从起点到目标点的全局路径。

改进的人工势场算法利用若干中间点来进行各局部路段的规划，由于每段局部路径之间不存在新的障碍物以及新的中间点，因此规划过程中不会出现死锁现象；同时由于改进算法中取消了障碍物的斥力作用，因此只在引力场作用下的机器人可以紧贴障碍物运动，从而获得长度更短的局部路径。

3 基于改进蚁群算法的全局最优路径规划

由于人工势场算法在进行路径规划时只考虑局部障碍物的影响，因此其计算量小、规划速度快，但其所得的路径却不具备全局最优特性。为了获得全局最优路径，往往还需借助其他全局规划算法做进一步的路径规划，其中蚁群算法因其简单、智能等特性而受到广泛应用[21-23]。

3.1 蚁群算法的基本原理

蚁群算法最早由DORIGO等[31]于1996年提出，并首先使用在解决旅行商问题上。它模拟蚂蚁觅食的过程，通过蚂蚁群体与环境之间的信息交互来实现最优路径搜索。

蚁群算法涉及到两个关键的步骤：概率选择和信息素更新[23]。所谓概率选择，是指每只蚂蚁在经过路口时都按一定的概率去选择下一个将要访问的节点。蚁群算法采用伪随机比例原则来选择下一个节点的位置，其路径选择规则为

(17)

其中

(18)

ηij(t)=1/djg

(19)

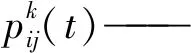
ak——蚂蚁k下一步被允许访问的节点集合

τij(t)——t时刻蚂蚁从节点i转移到节点j的信息素浓度

τis(t)——t时刻蚂蚁从节点i转移到节点s的信息素浓度

ηij(t)——t时刻蚂蚁从节点i转移到节点j的启发信息

ηis(t)——t时刻蚂蚁从节点i转移到节点s的启发信息

α——信息素启发因子

β——期望启发因子

q——均布在[0,1]区间的随机变量

q0——概率常数，q0∈[0,1]

J——随机变量，由式(17)的概率分布而产生

djg——节点j到目标节点g的欧氏距离

所谓信息素更新，是指蚂蚁在访问过的节点中会留下一种被称为信息素的物质，其大小与蚂蚁所走过的路径长度有关。通过各节点上信息素的累积和挥发，可引导后续蚂蚁进行路径选择，从而寻找一条最优的路径。为了兼顾全局搜索和局部搜索的能力，基本蚁群算法采用全局信息素更新和局部信息素更新的策略，相应的公式为

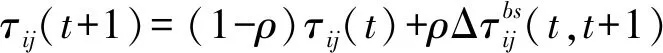
(20)

τij(t+1)=(1-ε)τij(t)+ετ0

(21)

式中ρ——全局信息素挥发系数，ρ∈(0,1]

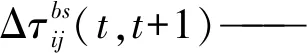
Tbs——蚁群单次迭代完成后搜索到的最优路径

ε——局部信息素挥发系数，ε∈(0,1]

τ0——初始信息素

由式(20)知，全局更新的作用是使最优路径中各节点的信息素得到加强，以形成正反馈，从而加快算法收敛。由式(21)知，局部更新的作用是使蚂蚁每次所经过路径中的各节点信息素得到减弱，以减少蚂蚁重复访问的概率，从而增强算法的全局搜索能力。

3.2 蚁群算法的改进

由蚁群算法的路径选择规则式(17)、(18)可知，信息素浓度τij和启发信息ηij是决定蚂蚁进行路径选择的两个重要因素。在早期，由于路径点上的信息素浓度较低，因此起主要作用的是启发信息ηij，而传统蚁群算法中ηij只与待选节点到目标节点的欧氏距离djg有关，却忽略了障碍物的影响，从而导致某些环境中初始路径陷入局部最优的情况。在后期，启发信息的作用减弱，信息素的作用增强，虽然传统蚁群算法中采用局部信息素更新策略改善了算法后期的全局搜索能力，但同时也降低了算法前期的收敛性，从而使算法整体的收敛速度降低；同理，全局信息素更新策略虽然改善了算法前期的收敛性，但也影响了后期的全局搜索能力。基于此，本文对传统蚁群算法的启发信息和信息素更新策略进行相应改进。

3.2.1启发信息的改进

结合人工势场算法计算速度快的优点，在考虑障碍物的情况下，用改进人工势场算法得到的待选节点j到目标点g的距离rjg来代替传统的欧氏距离djg，同时为了更加准确地反映当前节点与目标节点的距离，将当前节点i与待选节点j的距离dij也考虑进来。此外，在算法后期，为了削弱启发信息的作用，以提高算法的全局搜索能力，引入一个启发信息诱导因子ζ，因此启发信息的改进公式为

(22)

式中NCmax——最大迭代次数

NC——当前迭代次数

ζ——启发信息诱导因子，ζ∈(0,1]

当ζ∈(0,0.5)时，算法早期，由于(1-ζ)/ζ>1，因此启发信息的作用将得到加强，从而有利于加快算法收敛速度；在算法后期，由于(NCmax-NC)/NCmax≪1，因此启发信息的作用将受到削弱，从而有利于提高算法的全局搜索能力。

3.2.2信息素更新策略的改进

由分析知，全局信息素更新和局部信息素更新各自所起的作用不同，然而在算法的整个过程中，不同阶段有不同的性能要求，因此固定式的全局更新和局部更新策略无法使算法的性能达到最优。基于此，本文提出了一种信息素更新的动态调整策略，其基本思想是在算法收敛速度较慢时，加强全局信息素更新的作用同时抑制局部信息素更新的作用，在算法收敛速度较快时，加强局部信息素更新作用同时抑制全局信息素更新的作用。全局信息素及局部信息素的更新公式如下

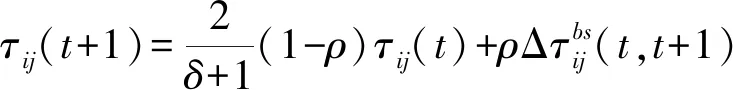
(23)

τij(t+1)=(1-ε)δτij(t)

(24)

其中

δ=NS/N0

式中δ——自适应变量N0——常数

由式(23)和式(24)知，当NSN0时，δ>1，则全局路径更新时最优路径中各节点信息素的增强效果将得到削弱，同时局部更新时蚂蚁所经历节点信息素的衰减效果将得到加强。以上对全局和局部信息素的自适应调整策略，相当于利用收敛次数构建了一条负反馈通道，以此保证全程中算法收敛速度和全局搜索能力的平稳和协调。

3.3 改进蚁群算法的具体步骤

图5为改进蚁群算法的流程图，具体步骤如下：

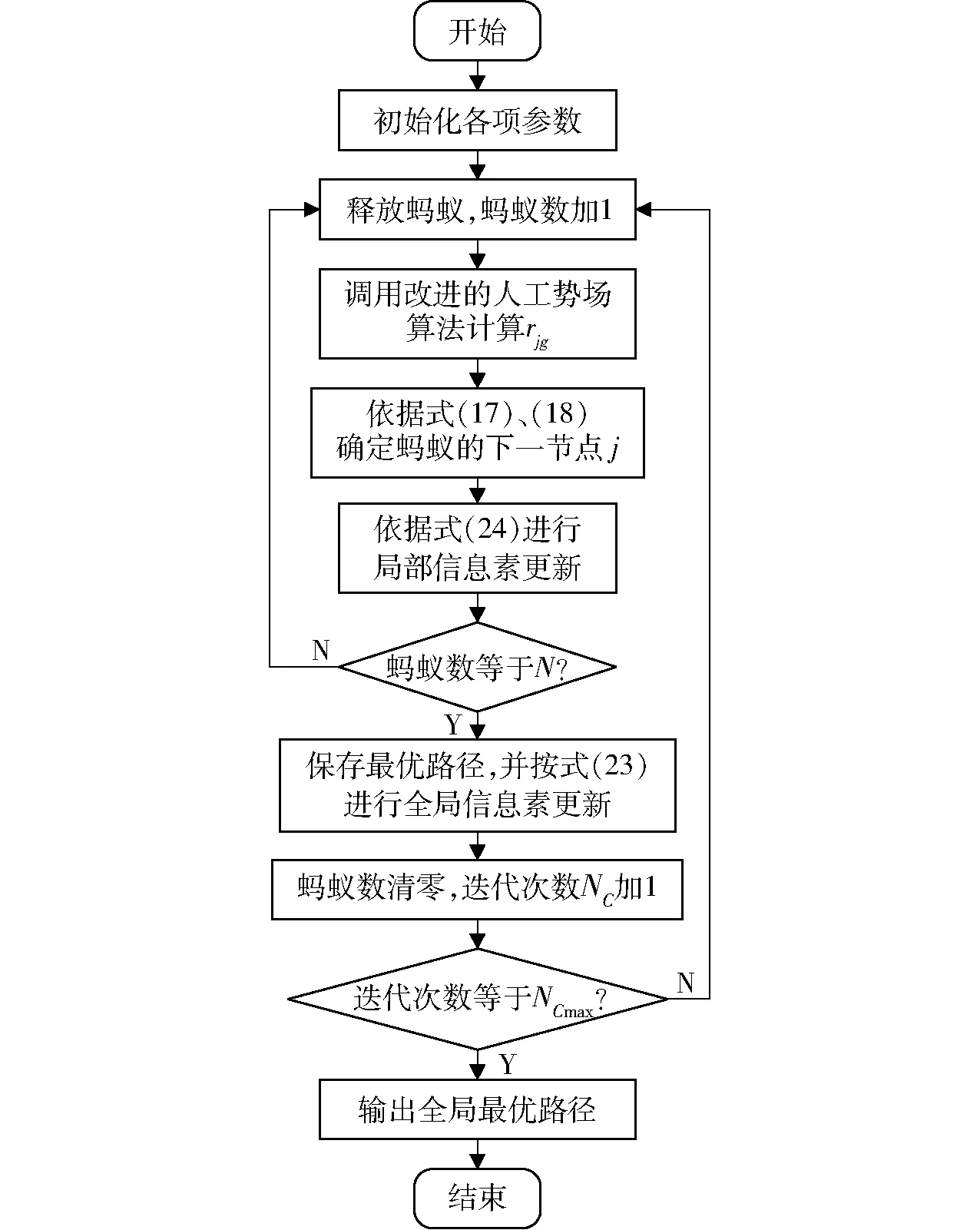
图5 改进蚁群算法流程图Fig.5 Flow chart of improved ant colony algorithm

(1)初始化各项参数：起始位置XS、目标位置XM、收敛计数器NS、迭代计数器NC，设置最大迭代次数NCmax、蚁群数量N、信息素启发因子α、期望启发因子β、启发信息诱导因子ζ、全局信息素挥发系数ρ、局部信息素挥发系数ε、信息素矩阵T及其他相关参数。

(2)蚁群路径迭代：从起点处释放N只蚂蚁，同时将起点位置XS放入禁忌表中，采用改进的人工势场算法计算出待选节点j到目标节点g的距离rjg，并代入式(22)中得到启发信息ηij(t)的值，再依据式(17)和式(18)确定下一个可行节点j，同时将所选的节点加入禁忌表中，按相同过程进行循环迭代直至蚂蚁到达目标点为止。

(3)更新局部信息素：蚂蚁每建立一条路径便按式(24)进行局部信息素更新。

(4)更新全局信息素：当N只蚂蚁的一次迭代完成后，找出最优路径，并按式(23)进行全局信息素更新。

(5)搜索结束判断：当单次迭代完成后，检测当前迭代次数NC是否等于最大迭代次数NCmax。如果相等，则结束算法并输出最优路径长度；如果不等，则跳转至步骤(2)。

4 仿真实验分析

为验证所述改进势场蚁群算法的有效性，在Matlab R2010a中进行仿真实验，计算机操作系统为Windows 7，CPU为Core i5-650，内存为8 GB，仿真环境为20×20的平面栅格环境，其中障碍物的设置如图2所示。同时，为了验证本文算法的优越性，在相同环境中将本文算法所得结果分别与基本蚁群算法以及文献[23]中改进蚁群算法的结果进行比较。

4.1 主要参数优化

蚁群算法中，影响其综合性能的参数有许多，由于这些参数之间存在紧密的耦合作用，因此很难通过理论的方式确定出最优参数组合[32-33]，目前常见的方法主要是通过多次实验进行反复试凑而得[18]。

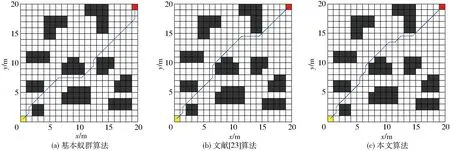
图6 简单环境中3种算法所得的路径规划结果Fig.6 Path planning results of three algorithms in simple environment

由于信息素和启发信息是影响蚂蚁进行路径选择的两个关键因素，因此本文重点考查与该两个因素有直接联系的5个参数：信息素启发因子α、期望启发因子β、启发信息诱导因子ζ、全局信息素挥发系数ρ、局部信息素挥发系数ε，其他参数的取值如表1所示。选取复杂仿真环境(图2b)，为避免偶然情况所引起的较大误差，对每组选定的参数组合进行10次仿真，并将所得结果求平均值后用于比较。为了避免仿真实验的次数过多，在各参数大致范围内选取5个点进行分析，分别为α∈{0,0.5,1,2,4},β∈{0,3,6,9,12},ζ∈{0.1,0.2,0.3,0.4,0.5},ρ∈{0.1，0.3，0.5，0.7，0.9},ε∈{0.1，0.3，0.5，0.7，0.9}。同时，为方便对单一的参数进行分析，设定一组默认参数值为：α=1，β=6，ζ=0.3，ρ=0.5，ε=0.5。每次实验时只改变其中一个参数的取值，其他4个参数均采用默认值，相应的实验结果如表2所示。

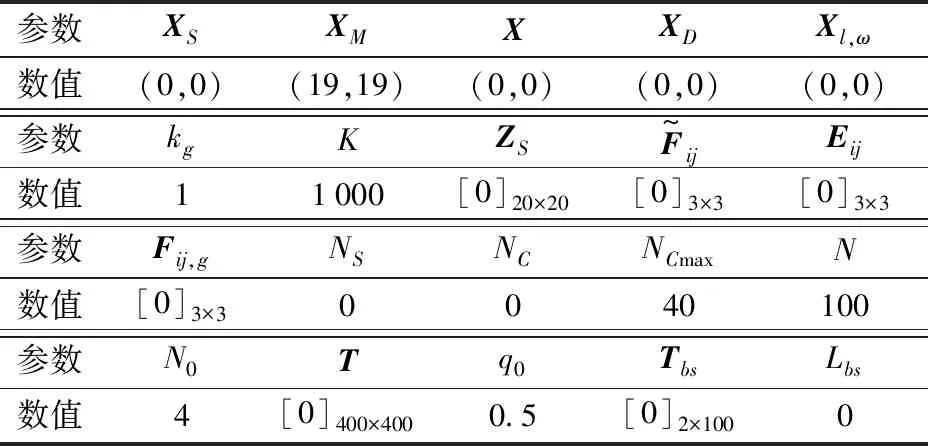
表1 本文算法涉及到的相关参数Tab.1 Parameters of proposed algorithm

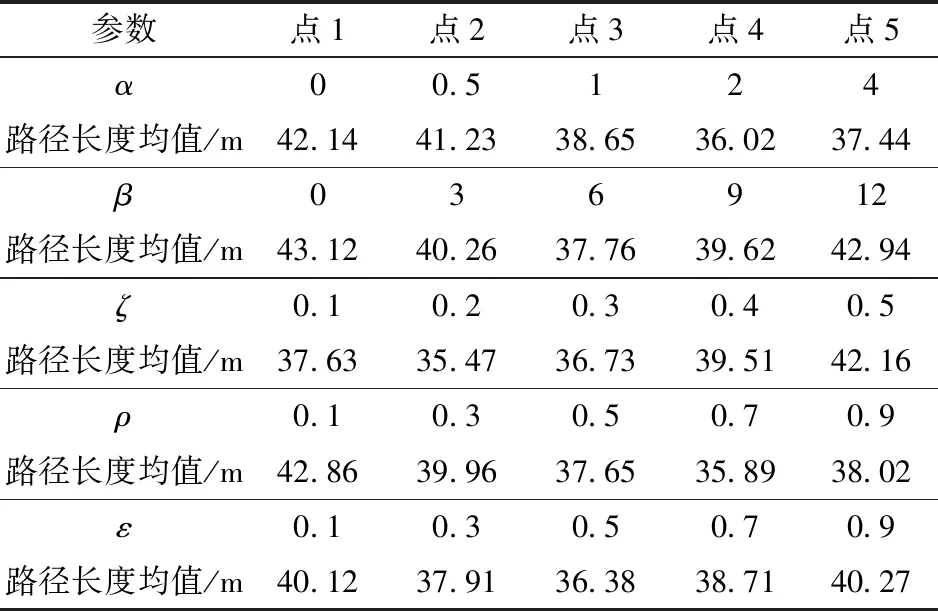
表2 主要参数优化实验结果Tab.2 Experimental results of main parameters optimization

由表2中的实验结果可知，参数α的最优值在2附近，参数β的最优值在6附近，参数ζ的最优值在0.2附近，参数ρ的最优值在0.7附近，参数ε的最优值在0.5附近，因此，针对本文所提的改进算法，其主要参数选取为：α=2，β=6，ζ=0.2，ρ=0.7，ε=0.5。

4.2 简单环境下的实验结果对比

在简单仿真环境中，由于障碍物设置较少，因此从实验结果可观察出每种算法的特点。在图2a所示的简单仿真环境中，3种算法的实验结果如图6和图7所示。

图7 简单环境中3种算法的收敛曲线Fig.7 Convergence curves of three algorithms in simple environment

由图6和图7知，基本蚁群算法在搜寻过程中陷入了局部最优解，其主要原因是在第1次避开中间凸形障碍物的过程中，受启发信息的误导，致使蚂蚁选择了距目标点欧氏距离较小的右边节点，后续在正反馈的作用下使蚁群搜索的路径不断收敛于该局部解。由于文献[23]和本文所述的算法对蚁群的启发信息进行了改进，所以避免了这种问题，同时由于人工势场算法为蚁群提供了较为正确的初始启发信息，致使蚁群获得了较优的初始路径，从而提高了算法的收敛速度。但是由于文献[23]采用传统人工势场算法来构建启发信息，导致蚁群的初始路径与最优路径相差较大，从而影响了算法后续的收敛速度。相比较而言，本文所述的算法由于对传统人工势场算法进行了改进，因此提高了初始路径的最优性，从而大大提高了算法的收敛速度。从图7可知，在简单环境中，由于利用改进人工势场算法所规划出的路径恰为最优路径，因此使蚁群算法在进行3次迭代之后即收敛于最优解。如表3所示，在简单环境中，相较于另外两种算法，本文算法不仅具有较高的收敛速度，同时运行时间也最短，为0.892 s。

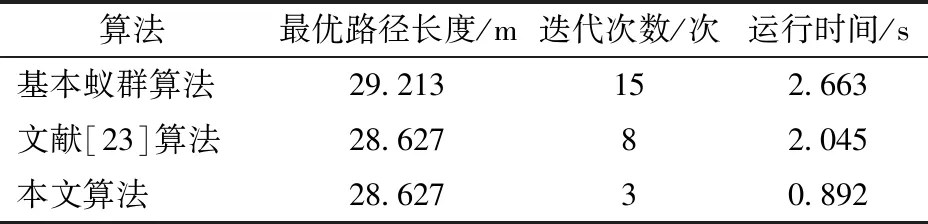
表3 简单环境中3种算法仿真结果对比Tab.3 Simulation results comparison of three algorithms in simple environment

4.3 复杂环境下的实验结果对比

为了解算法在复杂环境中的适用情况，在图2b所示的复杂环境中对3种算法进行仿真实验，结果如图8、9所示。

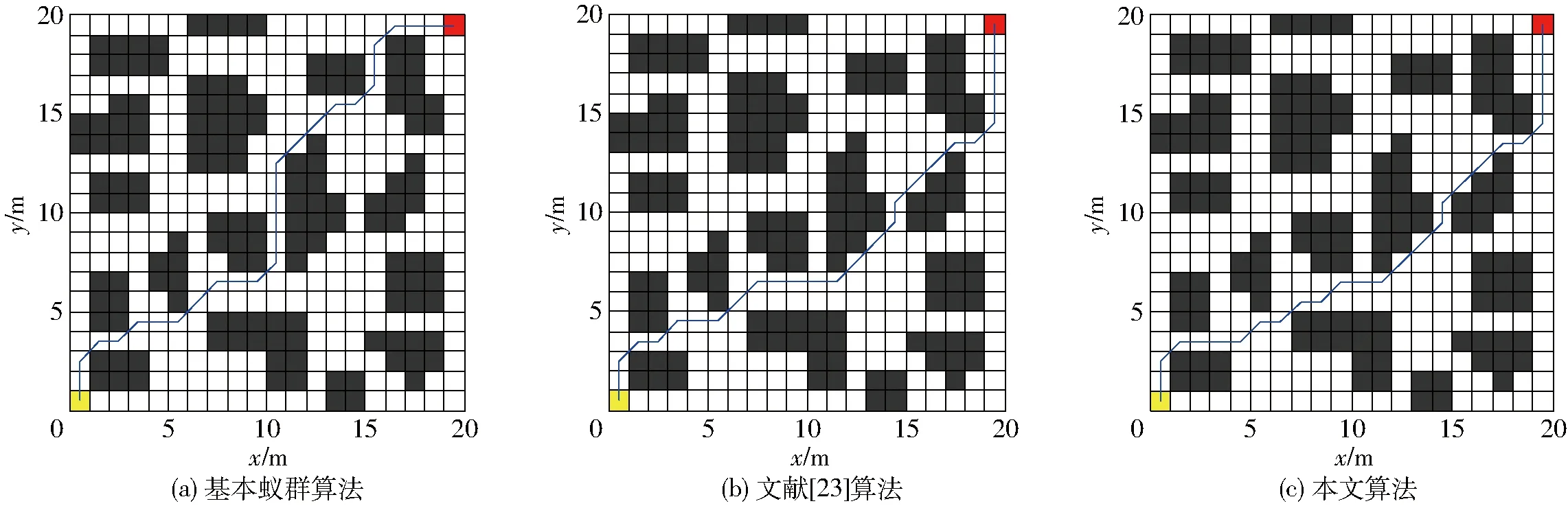
图8 复杂环境中3种算法所得的路径规划结果Fig.8 Path planning results of three algorithms in complex environment

由图8和图9可知，在复杂环境中基本蚁群算法搜索到的路径仍陷入了局部最优的情况。本文算法搜索到的最优路径长度与文献[23]算法搜索到的路径长度一致，均为31.556 m。但是由于本文算法采用改进后的人工势场算法来启发蚁群进行搜索，因此初始路径明显优于文献[23]算法的初始路径。本文算法初始搜索到的路径长度为38.314 m，而文献[23]算法初始搜索到的路径长度为40.142 m。

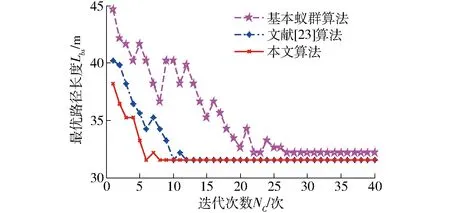
图9 复杂环境中3种算法的收敛曲线Fig.9 Convergence curves of three algorithms in complex environment

另外，在算法迭代过程中，由于全局信息素和局部信息素的交替作用，致使算法收敛曲线存在一定的波动性，严重影响了算法的收敛速度。在本文算法中，由于利用收敛次数构建了一条负反馈通道，因此有效降低了算法迭代过程中的波动性，使算法的收敛过程趋于平稳，从而提高了算法的收敛速度。在38.314 m这一相同的初始路径长度下，本文算法只需经过8次迭代即可收敛到最优解，文献[23]算法需要进行10次迭代方可收敛到最优解，而基本蚁群算法至少需要进行15次迭代方可收敛到最优解。

此外，从表4中可以看出，本文算法进行最优路径规划的时间明显低于其他两种算法，其中除了本文算法的迭代次数较少之外，还因为在改进的人工势场算法中省去了对无效障碍物以及斥力场的计算，因此有效减少了算法的计算量，从而缩短了算法的运行时间。

为了进一步了解本文算法的全局搜索能力，在相同的复杂环境中，分别导出3种算法中所有蚂蚁的搜索路径，如图10所示，其中蓝色粗实线表示对应算法所得的最优路径。为了量化算法的全局搜索能力，用蚁群所寻路径对环境的覆盖率φ来表示，

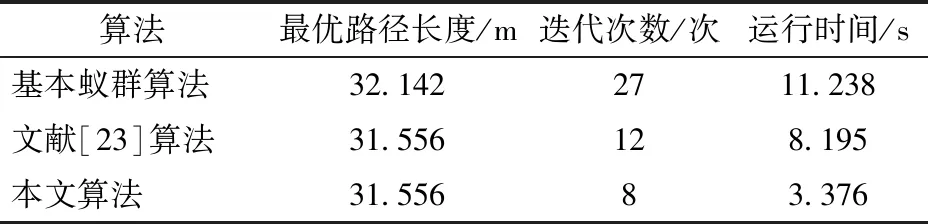
表4 复杂环境中3种算法仿真结果对比Tab.4 Simulation results comparison of three algorithms in complex environment

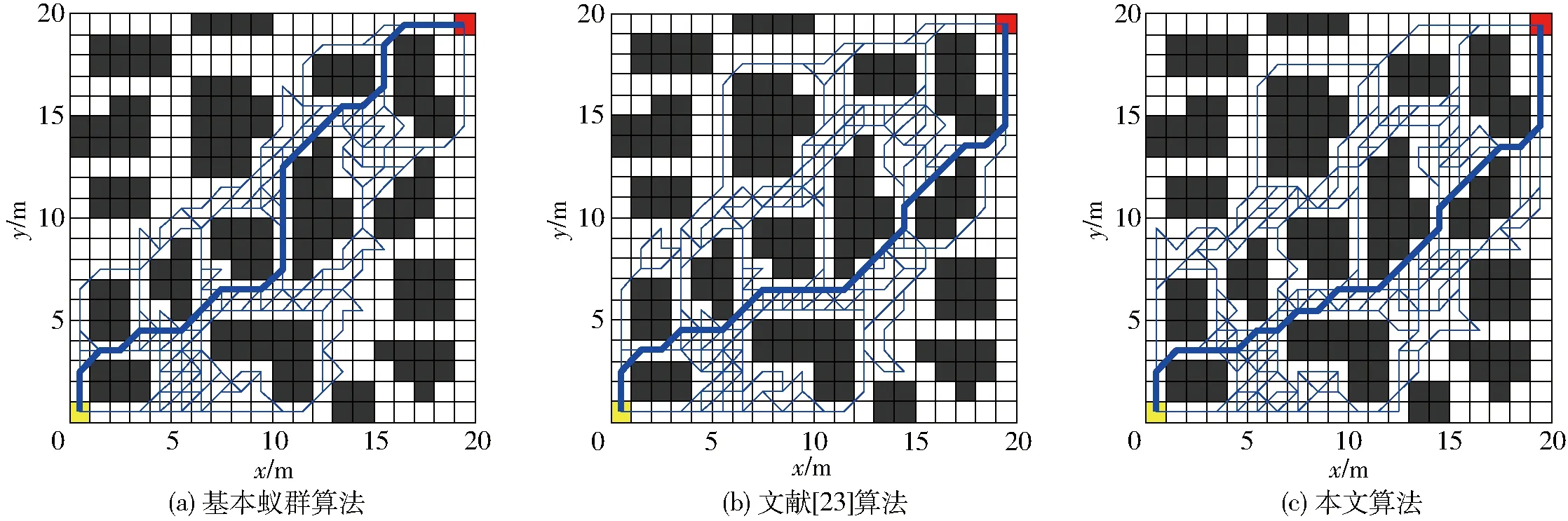
图10 3种算法的全局搜索结果对比Fig.10 Global searching result comparison of three algorithms

计算公式为

(25)

式中Npass——蚁群搜索到的栅格个数

Nfree——环境中自由栅格的个数

由图10可知，文献[23]和本文算法中蚁群搜索的环境范围明显较基本蚁群算法中蚁群搜索的范围广，因此该两种算法找到最优路径的可能性更高。由式(25)计算可得，基本蚁群算法所寻路径对环境的覆盖率为57.09%，文献[23]算法所寻路径对环境的覆盖率为72.83%，本文算法所寻路径对环境的覆盖率为73.63%。因此，本文算法所寻路径对环境的覆盖率最大，搜寻到最优路径的可能性也最大，故而相应的全局寻优能力最强。

5 结论

(1)通过理论分析，发现传统人工势场算法存在死锁及局部路径欠优等问题，利用其规划的结果作为先验知识启发蚁群进行初始搜索，会降低初始路径的优越性。因此，本文对传统人工势场算法进行了改进，通过障碍物检测算法识别有效障碍物和路径中间点，并用障碍物边界条件替换原有的斥力场函数。仿真实验表明，利用改进人工势场算法的结果启发蚁群进行搜索，可以提高蚁群算法初始路径的优越性。

(2)针对基本蚁群算法中全局信息素和局部信息素的内在矛盾，提出一种新的信息素更新策略，以收敛次数构建一条负反馈通道，以便根据收敛次数的变化来动态调整全局信息素和局部信息素的更新速度，从而保证全程中算法收敛性和全局搜索能力的协调与统一。

(3)采用组合实验的方法，对改进势场蚁群算法中的5个重要参数进行优化，获得了一组较优的参数组合方案：α=2，β=6，ζ=0.2，ρ=0.7，ε=0.5。

(4)采用栅格法构建机器人的两种环境模型，并在Matlab中对基本蚁群算法、文献[23]算法以及本文算法进行相同的仿真对比实验，结果表明，本文算法的运行时间最短，收敛速度最快，全局寻优能力最强。