中国企业部门信用风险溢价期限结构与宏观经济因子

张亦春,陈 华,郑晓亚

(1.厦门大学经济学院，福建 厦门 361005；2.中国人民银行数字货币研究所，北京 100800；3.中国建设银行股份有限公司，北京 100033)

1 引言

自2008年国际金融危机爆发以来，中国企业部门杠杆率水平快速上升。2013年中国企业部门债务余额68.06万亿元，与当年GDP的比率为120%，远超经济合作组织(OECD)国家90%的阀值。近年来，中国企业部门债务风险不断暴露，企业信用评级下调、企业债务违约、理财产品延期兑付等事件频繁发生。尤其是在2013年6月20日，中国银行间市场爆发严重的“钱荒”现象，流动性突然匮竭，资金利率水平飙升，隔夜回购利率一度达到30%。“钱荒”的发生进一步加剧了市场对中国明斯基时刻(Minsky Moment)即将来临的担忧。中国企业部门债务周期是否即将步入去杠杆化阶段，是否会引致系统性信用危机，正成为学界、业界和监管者关注的焦点。

中国企业部门债务风险累积与暴露背后的经济现实是，中国经济增速正由过去两位数的高速增长期转入一位数的中速增长期。在这一转换的过程中，多方面的宏观经济和政策因素在发挥着不同的作用。供给层面，中国15至59岁劳动年龄人口于2010年开始负增长，人口抚养比不再降低，在经过刘易斯拐点并且人口红利面临消失的情况下，中国通过劳动力在部门间的转移所获得的资源重新配置效应，以及劳动力无限供给所赢得的稳定的资本报酬效应，都将逐渐消失[1]，由此，中国潜在经济增长率将会下降为“十二五”期间的7.2%和“十三五”期间的6.1%[2]。同时，资源约束和生态环境恶化压力使得粗放型经济增长模式难以为继。需求层面，消费与投资比重失衡带来的去产能化压力正不断上升，特别是在“潮涌现象”严重的钢铁、水泥、煤化工、多晶硅、电解铝、风电设备等行业，产能过剩问题尤为严重[3]。在去产能化压力下，企业的内生性投资动力不足，制造业和房地产投资增速下滑趋势明显，而受制于有限的财政政策空间，政府主导的基础设施投资也难以继续成为投资回升的支撑动力。在政策上，政府提高了短期经济下行的容忍度，不再推出大规模的经济刺激计划，而是力图通过主动的制度改革和结构调整，来提高资源配置效率，增强经济内生增长动力，从而实现经济的长期可持续增长。

正是基于上述“增长速度进入换挡期、结构调整面临阵痛期、前期政策消化期”等三期叠加中的宏观经济环境，中国企业部门债务风险的暴露呈现出区域性、行业性特征，甚至存在着向系统性危机发展的隐患。温州企业家集体“跑路”、光伏产业大规模破产、钢贸行业深陷债务危机等大面积违约事件已给予充分的彰显。因此，观察和理解中国企业部门债务风险，需要宏观的经济视角，而不仅仅是停留在企业的微观层面。

研究文献亦表明，除了企业的个体因素(Firm specific factor)，企业的违约风险还取决于共同因素(Common factor)。Moore[4]研究显示，企业破产的概率会随着经济周期的变化而变化，在经济繁荣时期企业破产的可能性较小，信用风险较小。Guha和Hiris[5]的研究也表明，在经济衰退时期，不同信用等级的公司债券的信用利差趋于扩大，而在经济扩张时期，信用利差则从前期高峰值趋于降低。Duffee[6]发现无风险利率和企业债券收益率溢价之间存在着负相关性。Jonathan[7]的研究显示，长期债券和短期债券的信用利差都会受到通货膨胀率的影响。因此，在信用风险模型中，纳入宏观因素尤为必要。

回顾国内文献，已有研究主要是基于企业微观层面的数据，应用Z-score模型、Logistic模型和Merton结构模型对中国企业部门信用风险进行研究，比如方洪全和石勇[8]、石晓军和任若恩[9]、李晓庆等[10]、马若微[11]、孔德营和李晓峰[12]等，存在着明显的不足：第一、尚未见基于简约模型的中国企业部门信用风险溢价期限结构研究。与Z-score模型、Logistic模型和Merton模型相比，Jarrow和Turnbull13]、Madan和Unal14]、Duffie和Singleton[15]的简约模型能够描述不连续、突发的违约事件，尤其是将违约设定为由外生的随机变量驱动，使得模型的应用更为灵活，可以纳入宏观经济信息，而不仅仅是在获取上存在一定困难的企业资产价值、资产收益波动率、资本结构等微观信息。第二、虽然周宏[16]的研究表明宏观经济不确定性对中国企业债券信用风险存在显著的影响，但他们只是进行简单的面板回归，缺乏经济理论基础，未能揭示宏观经济变化在中国企业部门信用风险中的定价及其影响机理。

鉴此，本文着眼于中国企业信用风险溢价变化的宏观经济因素，在简约模型的基础上引入结构向量自回归模型(SVAR)，将经济冲击区分为总供给冲击、总需求冲击和货币政策冲击，以此研究各类经济冲击对中国企业信用风险溢价的影响特征，从而揭示中国企业部门信用风险定价的宏观经济机理。

本文的主要研究贡献是：第一、迄今为止，国内外文献尚未见基于简约模型的中国企业部门信用风险溢价期限结构研究，对此，本文进行了突破。第二、已有文献主要采用企业微观层面的Z-score模型、Logistic模型和Merton结构模型来研究中国企业部门信用风险，忽视了中国企业信用风险变化背后的宏观经济现实，而本文的研究则是从宏观层面研究各类宏观经济因子在中国企业部门信用风险溢价期限结构的定价，弥补了已有研究不足。第三、本文的研究将影响中国企业部门信用风险溢价变化的宏观经济因子具体化为总供给冲击、总需求冲击和货币政策冲击，使得模型的研究结论富有政策涵义，有助于我们理解当今中国企业部门信用风险的宏观成因和变化规律，从而为相关政策的制定和实施提供更全面的参考依据。

2 研究模型与方法

2.1 简约模型

延续已有简约模型的思路，我们假定信用风险债券的违约时点不可预测，并存在瞬时违约的可能性。用以下形式的随机变量H(t)表示在t时刻之前信用风险零息票债券是否发生违约。

(1)

其中Γ代表企业违约的第一个时点。假定h(t)为H(t)的强度过程(Intensity Process)，h(t)Δ代表在[t,t+Δ]期间信用风险零息票债券发生违约的近似概率。进一步地，同Duffie和Singleton[15]一样，我们假定当信用风险零息票债券发生违约，投资者仅能得到债券市场价值的1-L(t)，其中L(t)代表违约损失率。

根据无套利定价理论，在风险中性测度Q下，无风险零息票债券和信用风险零息票债券价格可分别表示为

(2)

V(t,T)=

(3)

以上式子可写成离散的递归定价形式，即

Pt=EQt[exp(-rt)*Pt+1]

(4)

Vt=EQt[exp(-rt-htLt)*Vt+1]

(5)

根据Radon-Nikodym定理，风险中性测度和现实测度可通过Radon-Nikodym导数φt+1进行转换。具体而言，对于t+1期的某随机变量St+1，EQt(St+1)=Et(St+1φt+1)/φt。基于标准的无套利仿射模型，φt+1可表示为

(6)

其中λt为与风险源ut+1有关的风险价格，于是定价核(Pricing Kernel)Mt+1表示为

(7)

进而，我们假定风险价格λt可表示为关于债券风险定价因子Ft的仿射函数

λt=λ+∧Ft

(8)

其中Ft为(M×1)状态向量，我们将其设定为由两个可观察的宏观经济变量——实际产出增速gt和通货膨胀水平pt，以及一个不可观察的潜在因子(Latent factor)fl组成。

(9)

并且，我们还假定，基于现实测度，Ft服从滞后1阶的高斯VAR过程：

Ft+1=c+ρFt+Σut+1

(10)

式中ut～i.i.d.N(0,IM)，Σut+1是对状态向量Ft的外生冲击，Σ为相应的协方差矩阵。基于风险中性测度Q，(10)式可表示为

Ft+1=cQ+ρQFt+ΣuQt+1

(11)

其中uQt+1为Q测度下服从独立正态分布的残差向量，而且

cQ=c-Σλ

(12)

ρQ=ρ-Σ∧

(13)

同样，我们假定无风险利率rt也可表示为关于Ft的仿射函数

rt=δ0+δ′1Ft

(14)

结合(9)式，上式可近似理解为泰勒规则

rt=δ0+δ′fmfm+δ′flfl

(15)

那么根据Ang和Piazzesi[17]的研究，基于以上假定，n期无风险零息票债券收益率ynt为

ynt=an+b′nFt

(16)

其中an和bn服从以下迭代过程

(17)

(18)

对于信用风险零息票债券，我们假定(3)式中的htLt同样可表示为关于Ft的仿射函数

htLt=η0+η′1Ft

(19)

那么，与无风险零息票债券相似，信用风险零息票债券收益率为

(20)

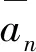
(21)

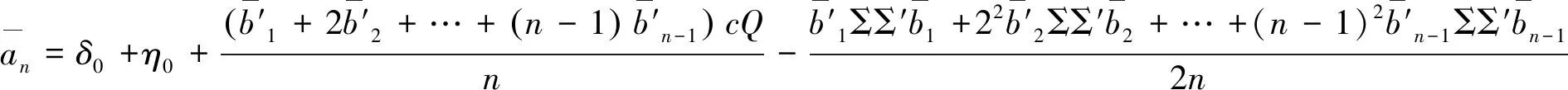
(22)

因此，n期限的信用风险溢价cspnt可表示为

(23)

最后，由于潜在因子fl经济含义模糊，因此参考Kaminska[18]的思路，我们引入经济含义更加清晰的向量Zt

(24)

那么基于(14)式不难得到

Zt=M0+MFt

(25)

其中

(26)

(27)

于是

Ft=M-1Zt-M-1M0

(28)

以及

Zt=M0+Mc-MρM-1M0+MρM-1Zt-1+MΣut

(29)

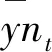
λt=λ+∧(M-1Zt-M-1M0)

(30)

rt=δ0+δ′1(M-1Zt-M-1M0)

(31)

ynt=an+b′n(M-1Zt-M-1M0)

(32)

(33)

(34)

2.2 SVAR模型的引入

参考Blanchard和Quah[19]的思路，我们假定经济向量Zt服从的一般VAR过程(见(29)式)等价于以下结构VAR过程

DZt=D0+D1Zt-1+εt

(35)

其中D对角线元素标准化为1，var(εt)=D2D′2，εt是由三种独立的经济冲击而组成的向量

(36)

其中ε1t为总供给冲击(Aggregate Supply Shock)，ε2t为总需求冲击(Aggregate Demand Shock)，ε3t为货币政策冲击(Monetary Policy Shock)。各经济冲击相互独立，因此协方差矩阵D2D′2为对角矩阵。根据宏观经济理论，我们可对(35)式的系数矩阵施加两个约束条件，来区分三类不同的经济冲击。

第一、短期约束条件。在冲击发生的当期，由于实体经济调整的时滞性，货币政策冲击ε3t对实际产出增速gt不存在影响，但对通货膨胀pt和无风险利率rt产生影响。相应的约束条件为

(37)

第二、长期约束条件。从长期来看，实际产出增速gt仅能由总供给ε1t决定，而总需求冲击ε2t和货币政策冲击ε3t对gt不具有长期影响。因此，存在约束条件

(38)

不难发现，Zt可表示成由上述三种经济冲击决定的形式

Zt=(D-D1)-1D0+(D-D1L)-1εt

(39)

2.3 估计方法与识别思路

本文对无风险零息票债券和信用风险零息票债券收益率进行联合估计，(16)和(20)式写成

(40)

根据Chen和Louis[20]、Ang和Piazzesi[17]等的研究，如果无套利仿射模型中存在Nl个潜在因子，那么在估计时，可假定Nl个无风险零息票债券收益率是无误差度量(Measured without Error)，而其余无风险零息票债券收益率和信用风险债券收益率则是有误差度量(Measured with Error)。因此，(40)式可进一步写成

(41)

传统上，无套利仿射模型估计方法是最大似然估计(MLE)，但由于无套利仿射模型估计参数较多，且参数之间存在高度的非线性化关系，因此最优化过程比较艰难，尤其是MLE估计对估计初始值较为敏感，难以获得全局最优估计值(Ang和Piazzesi[17]；Kim[21])。对此，Hamilton和Jing[22]提出全新的估计方法。他们的研究证明，最小卡方估计法(Minimum-chi-square Estimation)渐进等价于MLE估计法，不仅估计简单，而且可以得到全局最优估计值。因此，本文采用Hamilton和Wu的最小卡方估计法对(1)至(34)式的无套利仿射模型进行估计。

最后，基于本文的研究目的，我们还需要从无套利仿射模型估计得到的一般VAR过程的(29)式识别出结构VAR过程的(35)式，对此，我们可通过以下识别条件进行识别。即基于估计得到的无套利仿射模型参数，建立(42)至(48)的方程组，求解得到D、D0、D1、D2。

1、D的对角线元素等于1

(42)

2、D2D′2为对角矩阵

(43)

3、D-1D0=M0+Mc-MρM-1M0

(44)

4、D-1D1=MρM-1

(45)

5、MΣ(MΣ)′=D-1D2(D-1D2)′

(46)

(47)

(48)

3 实证结果与分析

3.1 变量选取与数据处理

3.2 模型参数估计值

基于Hamilton和Jing[22]的最小卡方估计方法，本文估计得到(1)至(34)式的简约模型估计值，见表1。进而，本文利用Matlab的自带函数fsolve对(42)至(48)式进行编程求解，得到D、D0、D1、D2，结果见表2。

表1 简约模型的系数估计值及其标准差

注释：()为相应系数估计值的标准差。估计软件为Matlab2012。

表2 结构VAR模型参数的识别

注释：估计软件为Matlab2012。

3.3 信用风险溢酬期限结构与宏观定价因子：脉冲响应函数分析与成分分解

基于简约模型和SVAR模型参数的估计值，本文通过(24)、(34)和(39)式推算出各类经济冲击，结果见图1至图3。图1显示，总供给冲击不存在明显的季节性特征。在2008年第四季度和2010年第一季度，总供给冲击大幅下挫，与2008年美国金融危机爆发的经济现实以及2010年中国劳动力步入刘易斯拐点的判断[2]基本一致。图2、图3的总需求冲击和货币政策冲击表现出明显的季节性特征。总需求冲击很好地反映了2008年美国金融危机、中国为应对国际金融危机而进行的四万亿经济刺激、2010年欧洲债务危机等重要经济事件。对于货币政策冲击，我们将其进行季节性调整，然后与滞后4期的M2同比增速进行对比，发现货币政策冲击的整体走势与滞后4期的M2同比增速非常一致，见图4。因此，我们认为本文的估计模型是合理的。

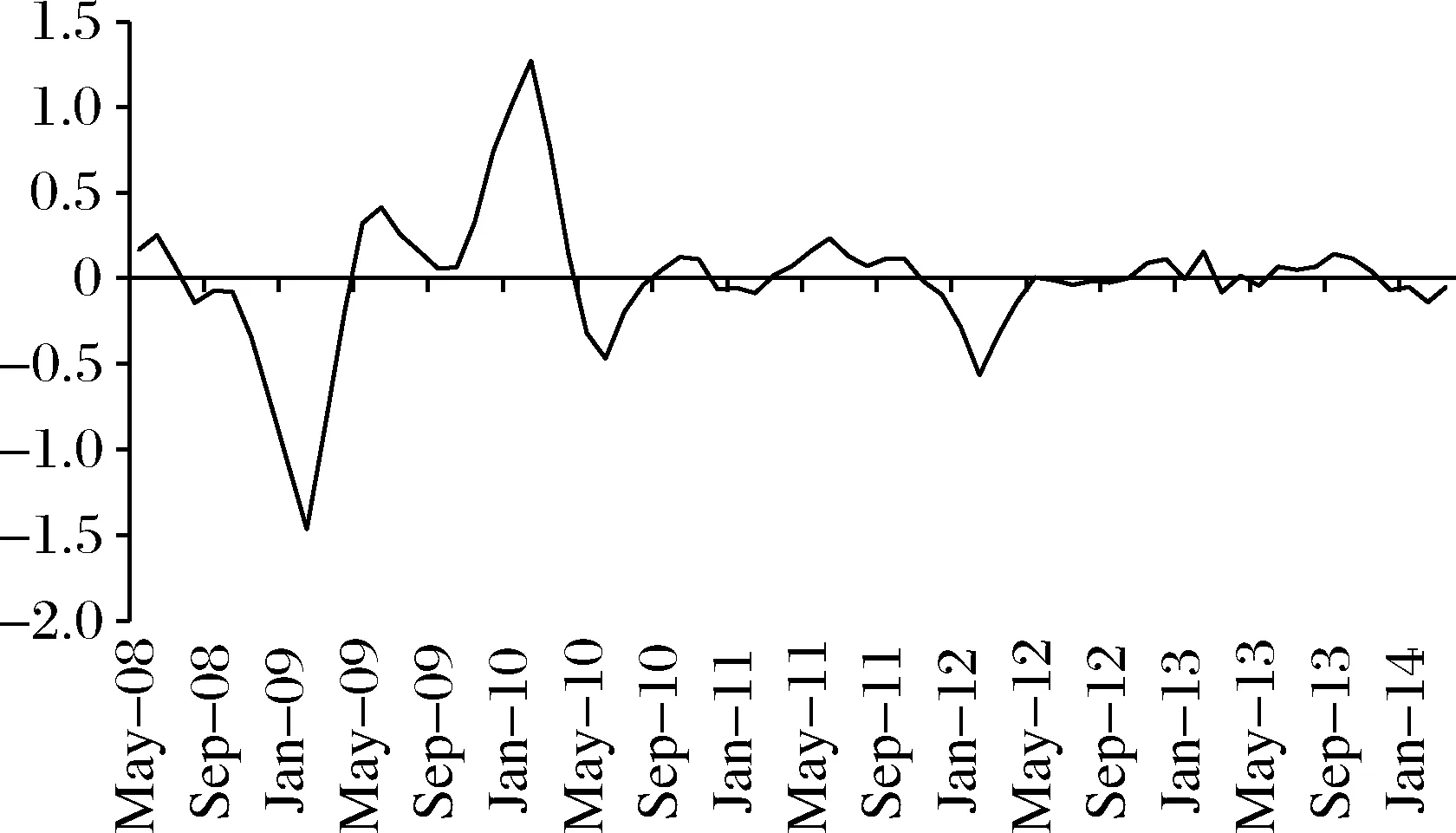
图1 总供给冲击

图2 总需求冲击

图3 货币政策冲击

图4 季节性调整之后的货币政策冲击与M2同比增速的对比

进而，根据(34)和(39)式，可以得到关于各类经济冲击对信用风险溢价期限结构的决定式(见下式)，以此进行脉冲响应函数分析和成分分解。

(49)

脉冲响应函数结果见图5至图13。图中结果显示，面对一个正向的总供给冲击，各期限各信用等级的信用风险溢价呈负向反应(见图5至图7)，即当总供给层面上出现技术进步、劳动力增加等正向冲击，将会带来整体信用风险溢价的下降，反之则会带来整体信用风险溢价的上升。与之不同，对于一个正向的总需求冲击，各期限各信用等级的信用风险溢价的反应却是正向(见图8至图10)，也就是说，社会总需求的增加(减少)将会使得中国企业信用风险溢价的上升(下降)。而面对一个正向的货币政策冲击，不同期限的信用风险溢价的反应方向存在差异：1年期的信用风险溢价呈正向反应，2年期和5年期的信用风险溢价则呈负向反应(见图11至图13)。这意味着，扩张性货币政策有助于降低长期限的信用风险溢价，而紧缩性货币政策将会推高长期限的信用风险溢价。

图5 不同期限的3A级信用风险溢价对总供给冲击的脉冲响应函数

图6 不同期限的2A级信用风险溢价对总供给冲击的脉冲响应函数

图7 不同期限的1A级信用风险溢价对总供给冲击的脉冲响应函数

图8 不同期限的3A级信用风险溢价对总需求冲击的脉冲响应函数

图9 不同期限的2A级信用风险溢价对总需求冲击的脉冲响应函数

图10 不同期限的1A级信用风险溢价对总需求冲击的脉冲响应函数

图11 不同期限的3A级信用风险溢价对货币政策冲击的脉冲响应函数

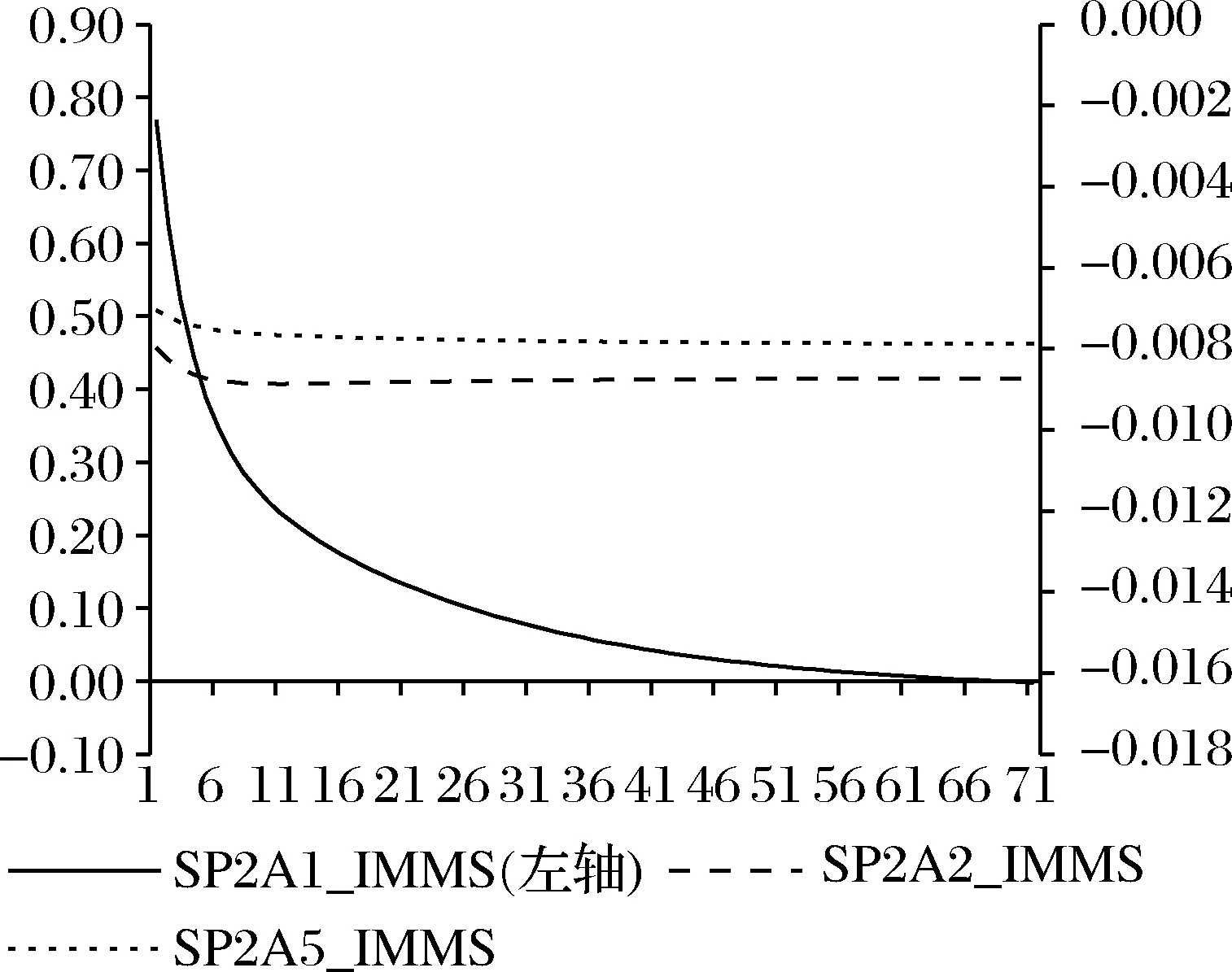
图12 不同期限的2A级信用风险溢价对货币政策冲击的脉冲响应函数

图13 不同期限的1A级信用风险溢价对货币政策冲击的脉冲响应函数

若比较不同信用等级不同期限的信用风险溢价的脉冲响应函数结果，我们可以发现，信用等级越低，期限越短，相应的信用风险溢价对各类经济冲击的反应程度则越大，也就是说，信用等级越低、期限越短的信用风险溢价，对宏观经济变化和政策调整越敏感，反之，信用等级越高、期限越长的信用风险溢价，对宏观经济变化和政策调整越不敏感。

同样基于(49)式，我们可以将不同期限不同信用等级的信用风险溢价分解为分别由总供给冲击、总需求冲击以及货币政策冲击决定的成分。

成分结果显示，不同期限不同信用等级的信用风险溢价的成分走势相似(结果备索)。因此，简洁起见，本文仅以对宏观经济变化和政策调整变化最为敏感的1年期1A级的信用风险溢价作为代表，分析宏观经济因子对中国企业信用风险溢价变化的影响与决定，见图14。图中，c1代表由总供给冲击决定的成分，c2代表由总需求冲击共同决定的成分，c3代表由货币政策冲击决定的成分。

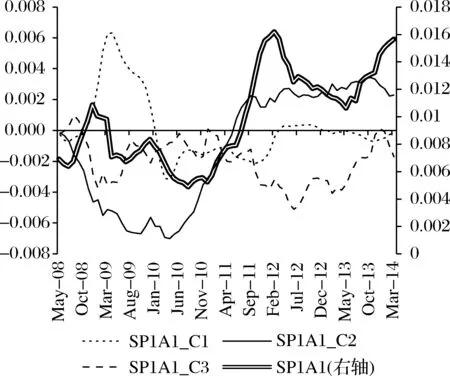
图14 1年期1A级信用风险溢价的成分分解

图中显示，1年期1A级的信用风险溢价在2011年7月之前普遍为负，而在2011年7月之后为正。将其进行成分分解，可以发现，在美国金融危机爆发的2008年，负向的总供给冲击使得信用风险溢价大幅上升，而在随后的2009年至2010年，由于正向的总供给冲击以及负向的总需求冲击，信用风险溢价不断下行。

但到2011年，信用风险溢价却大幅上升，由负的信用风险溢价逆转为正的信用风险溢价，背后的驱动因素是4万亿经济刺激计划所带来的正向总需求冲击。结合图2，我们可以看出，2010年4月至2011年9月的总需求冲击持续为正，因此大幅推动了信用风险溢价的上行，而在此阶段的总供给冲击和货币政策冲击对信用风险溢价的决定较弱。并且从2011年至今，由总需求冲击带来的信用风险溢价一直保持微弱的上行趋势，处于高位水平。因此可以判断，一直以来持续处于高位的信用风险溢价的主要根源是4万亿经济刺激计划所带来的扩张性总需求。

在经历2010年4月至2011年9月的上升之后，信用风险溢价不断下行，直至“钱荒”爆发时的2013年6月。图14的成分结果显示，此阶段的下行归因于2011年至2012年期间的正向货币政策冲击(见图4)，也就是说，2011年至2012年期间货币政策的扩张，降低了2010年至2011年社会总需求扩张所导致的高信用风险溢价水平。但从2013年年初开始，负向货币政策冲击开始推动信用风险溢价急剧上行，而相应阶段的由总供给冲击和总需求冲击带来的信用风险溢价却未大幅上升，因此我们可以判断，“钱荒”发生时信用风险溢价的大幅上升，并不是由宏观经济基本面变化而引起，而是由货币政策冲击所导致的结果。

比较各类经济冲击对信用风险溢价的影响，可以发现，总体而言，总需求冲击和总供给冲击对信用风险溢价的影响程度较大，而总供给除了在2009年对信用风险溢价产生较大影响之外，在其他期间对信用风险溢价的影响程度较小。图中显示，从2010年开始，总供给推动信用风险溢价缓慢上行。

4 结语

本文的研究旨在揭示中国企业部门信用风险溢价变化的宏观经济因素，从而更好地理解当前正在不断暴露的中国企业部门信用风险的宏观成因。本文在简约模型的基础上引入结构向量自回归模型(SVAR)，将经济冲击区分为总供给冲击、总需求冲击和货币政策冲击，利用脉冲响应函数和成分分解方法，研究各类经济冲击对中国企业部门信用风险的影响特征，得到以下主要研究结论：

第一，正向的总供给冲击和货币政策冲击有助于降低中国企业部门信用风险溢价，但正向的社会总需求则会推高中国企业部门信用风险溢价；第二，4万亿经济刺激计划所带来的扩张性总需求冲击，使得信用风险溢价在2011年由负逆转为正，并使其持续保持着高位水平；第三，2011年至2012年期间货币政策的扩张，降低了2010年至2011年社会总需求扩张所导致的高信用风险溢价水平；第四，“钱荒”发生时，中国企业部门信用风险溢价的大幅上升，并不是由宏观经济基本面变化而引起，而是由货币政策冲击所导致的结果；第五，从2010年开始，由于刘易斯拐点来临而带来的负向总供给冲击推动了信用风险溢价缓慢上行。

以上结论给我们的重要政策启示是，“钱荒”并不是中国明斯基时刻带来的前兆，而是货币政策调整的结果，但与此同时，我们应认识到，自2011年以来一直处于高位水平的信用风险溢价的根源却是4万亿经济刺激计划所导致的扩张性总需求，因此欲从根本上降低中国企业部门信用风险水平，避免系统性信用危机的发生，应紧缩社会总需求，并通过制度改革和结构调整，提高劳动生产率和资源利用效率，以此从总供给层面上，降低企业部门信用风险。