基于响应面法的无轨门机T型架优化设计

段启楠

（中铁四局集团有限公司第八工程分公司，安徽 合肥230041）

1 概述

随着我国无砟轨道技术的快速发展，国内厂家已研制成功多种无咋轨道机械并投入使用[1-3]。我国研制的无轨伸缩式门式起重机，在轨道施工中用于吊装轨枕等，是一种工作效率较高的无砟轨道机械。其中，T型架是无轨门机中的关键结构件，其结构性能决定了无轨门机施工的安全性。

目前，国内厂家对T型架的结构设计基本采用以经典力学与材料力学为基础的经验设计法。因没有相应的设计规范，考虑到安全问题，常选用较大的安全系数，导致了结构设计的冗余，使T型架质量偏大，因此拟对其结构进行轻量化研究[4]。

本文选用ISIGHT软件，先对T型架各设计参数进行试验分析，再将筛选出的关键设计参数代入构建的近似模型中进行优化设计，从而找到适用于T型架的结构优化方法。

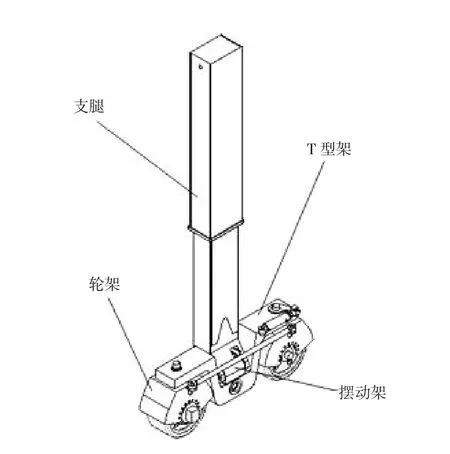
图1 无轨门机支腿结构简图

2 T型架优化模型的建立

图1为某公司设计的无轨门机支腿结构简图，可知T型架是连接轮架与摆动架的关键结构，其结构性能决定了无轨门机的整机性能。

以此T型架为例，T型架主要承受门机自重PG、起升小车自重GXC、水平惯性载荷PH和起升载荷Q的作用。考虑起升机构启制动引起结构振动产生的动力响应，取门机重力载荷为φ1PG，取小车自重载荷为φ1GXC，其中φ1为起升冲击系数。考虑吊重在起升时惯性力的作用，取起升载荷为φ2Q，其中φ2为起升动载系数。考虑门机行进过程中启动（制动）产生的水平惯性载荷PH。加速度值依据设计规范取a=0.12 m/s2，即惯性力 PH=1.5 ma=0.18 m。

根据设计要求，计算工况为载荷作用于摆动架销轴上计算结构刚度与强度。

2.1 设计变量

选择T型架的部分结构尺寸与板厚作为设计变量，如表1所示。

表1 优化变量

2.2 T型架数学模型

以T型架的刚度与强度为约束条件，T型架结构自重最轻为优化目标，建立如下数学模型：

1）优化目标

式中：T_MASS为T型架结构自重。

2）约束条件

式中：DG为T型架在工作状态下的最大垂直静刚度，[f]为T型架许用静刚度，根据设计要求，取2 mm；SG为T型架在工作状态下的最大等效应力，[σ]为材料许用应力，T型架的材料为Q345钢，安全系数取 1.34[5]，故[σ]=345/1.34=257 MPa；xl为设计变量的下限，xu为设计变量的下限，具体取值见表1。

2.3 T型架有限元模型

通过ANSYS中的APDL语言定义T型架的各设计参数，选用SOLID45单元模拟T型架的整体结构，建立的T型架结构有限元模型如图2所示。整个系统离散成247 232个单元，65 503个节点，各构件的材料均为Q345钢，其弹性模量EX=2.1×1011N/m2，泊松比 μ =0.3，材料密度 ρ=7 850 kg/m3。

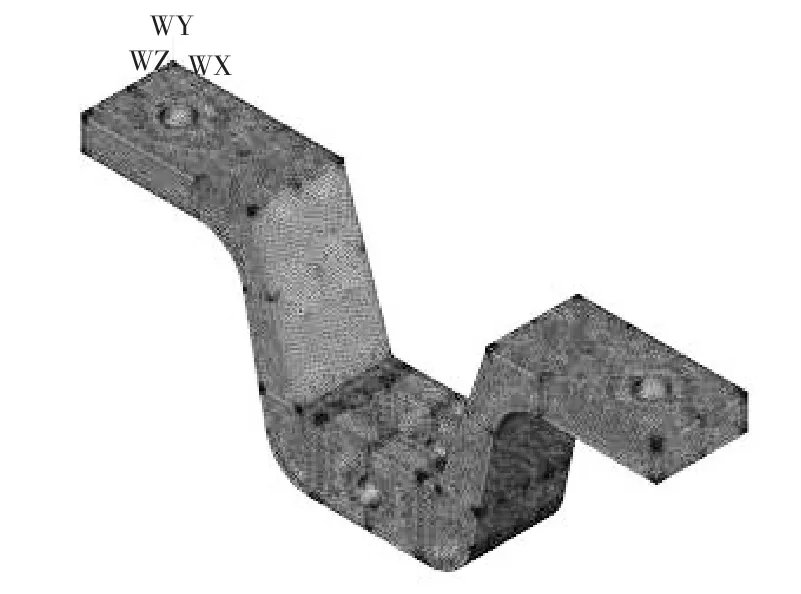
图2 T型架结构有限元模型

3 T型架轻量化设计

ISIGHT是一种功能强大的计算机辅助优化软件[6]，广泛应用于航空航天等领域的零部件与子系统的优化[7]。利用ISIGHT与其他CAD/CAE软件的集成，通过管理复杂的仿真流程，运用多种优化方法自动探索得到优化方案，可以缩短产品的研发周期，降低研发成本。

T型架的轻量化设计流程：首先在ANSYS软件中用APDL语言构建T型架的有限元模型，将其集成到ISIGHT软件中，选用最优拉丁超立方设计方法生成设计变量的初始样本点，其次进行试验分析筛选出对T型架的结构刚度、强度以及自重影响较大的设计变量，然后以T型架结构刚度与强度为约束条件，以T型架质量最轻为目标构建响应面近似模型，最后选用多岛遗传算法对响应面模型进行全局寻优。

3.1 试验分析

考虑到已确定的设计变量个数较多，为了提升优化效率，降低计算成本，故选用ISIGHT软件中的试验分析来确定对T型架的刚度、强度以及结构自重响应灵敏度较高的设计变量。在试验分析之前，选用最优拉丁超立方设计方法生成初始样本数据点。

采用最优拉丁超立方设计方法，生成150个初始样本点进行试验分析，结果如图3所示。

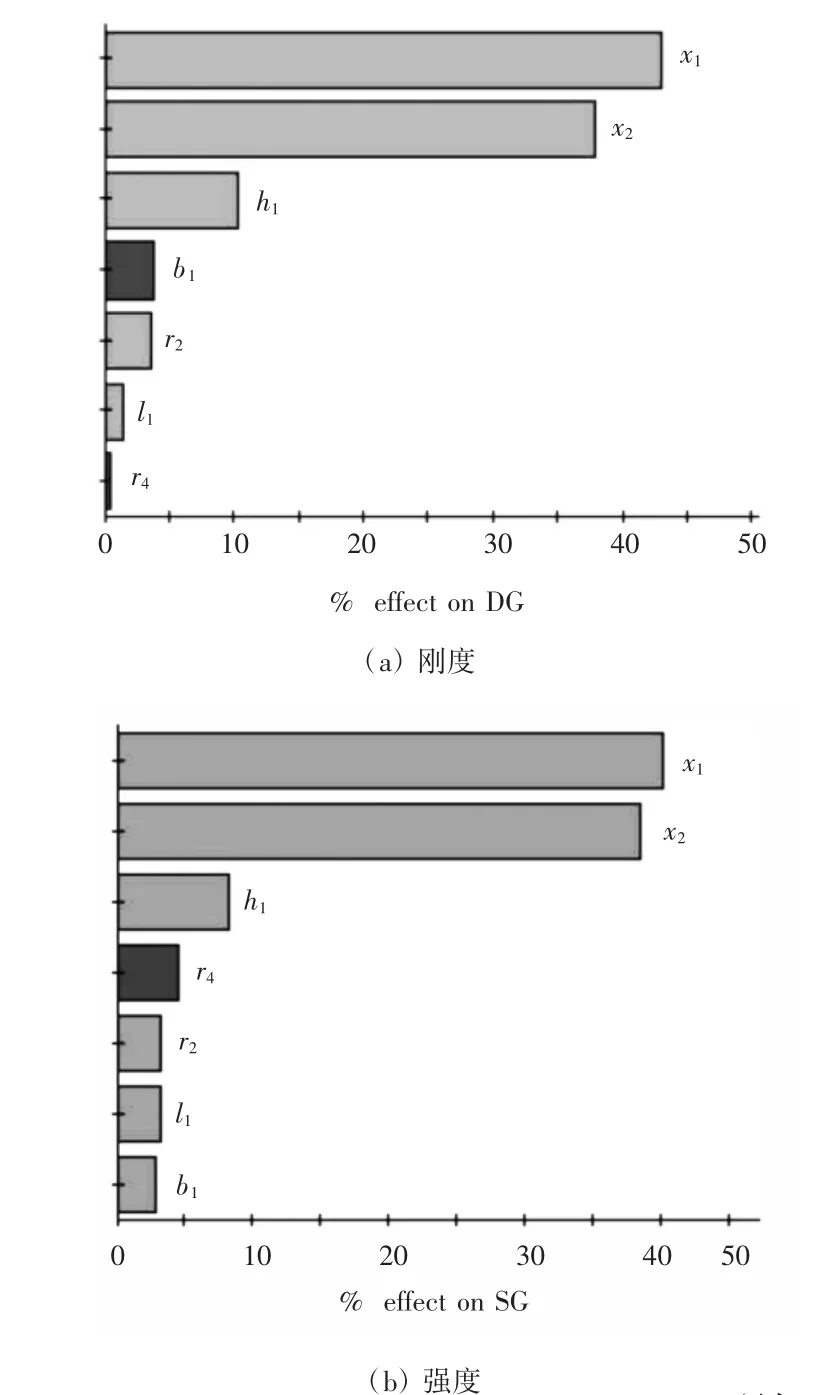
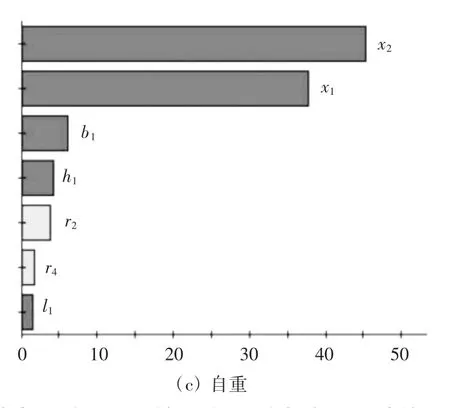
图3 设计变量对T型架的刚度、强度与自重影响的Pareto图

由图3可知，设计变量x1，x2，h1对T型架的结构刚度影响较大，设计变量x1，x2，h1对T型架的结构强度影响较大，设计变量x1，x2，b1对T型架的结构自重的影响较大。综合考虑，选取 x1，x2，h1，b1为最终设计变量来构建响应面近似模型，进而提升优化效率，降低计算成本。

3.2 响应面近似模型的构建

响应面近似模型的构建方法就是利用数学多项式函数来拟合较为复杂的设计空间，不仅能得到最优的设计变量组合来逼近目标函数[8]，还能拟合复杂的响应关系[9]，这为优化设计提供了有效的途径。

构建响应面近似模型的过程如下：先确定响应面模型基函数的个数；其次在设计空间内生成样本设计点，通过对样本设计点的计算，得到一系列真实响应值；然后通过最小二乘法确定响应面近似模型多项式的待定系数[10]；最后得到响应面近似模型。

在构建响应面近似模型时，将试验分析筛选出的4个最终设计参数作为输入参数，以DG，SG和T_MASS作为输出响应，为了提高模型的可信度，选用100个试验样本点，并且随机选取15个点作为误差分析样本点，通过ISIGHT软件对其进行误差分析，结果如表2所示。

表2 响应面近似模型的误差评估结果

由表2可知，响应面近似模型的R2误差、均方根值、平均误差与最大误差均在误差允许范围之内，故此响应面近似模型具有较高的精度，可用于优化设计。

3.3 优化分析

优化设计的本质是通过不断的搜索与迭代得到模型的最优解，但传统的梯度优化与直接搜索方法常得到局部最优解，多岛遗传算法是对传统遗传算法的改进，具有更强的全局求解能力与计算效率[11]。因此，本文选用多岛遗传算法来进行全局寻优。

在采用多岛遗传算法进行全局寻优之前，设定子群规模为10，岛的个数为10，整个过程的进化代数为100，设定交叉概率为0.8来保证搜索顺畅，设定变异概率为0.08来维持种群的多样性。T型架目标函数的寻优历程如图4所示。由图可知，当T型架近似模型迭代至1348次时获得全局最优解。

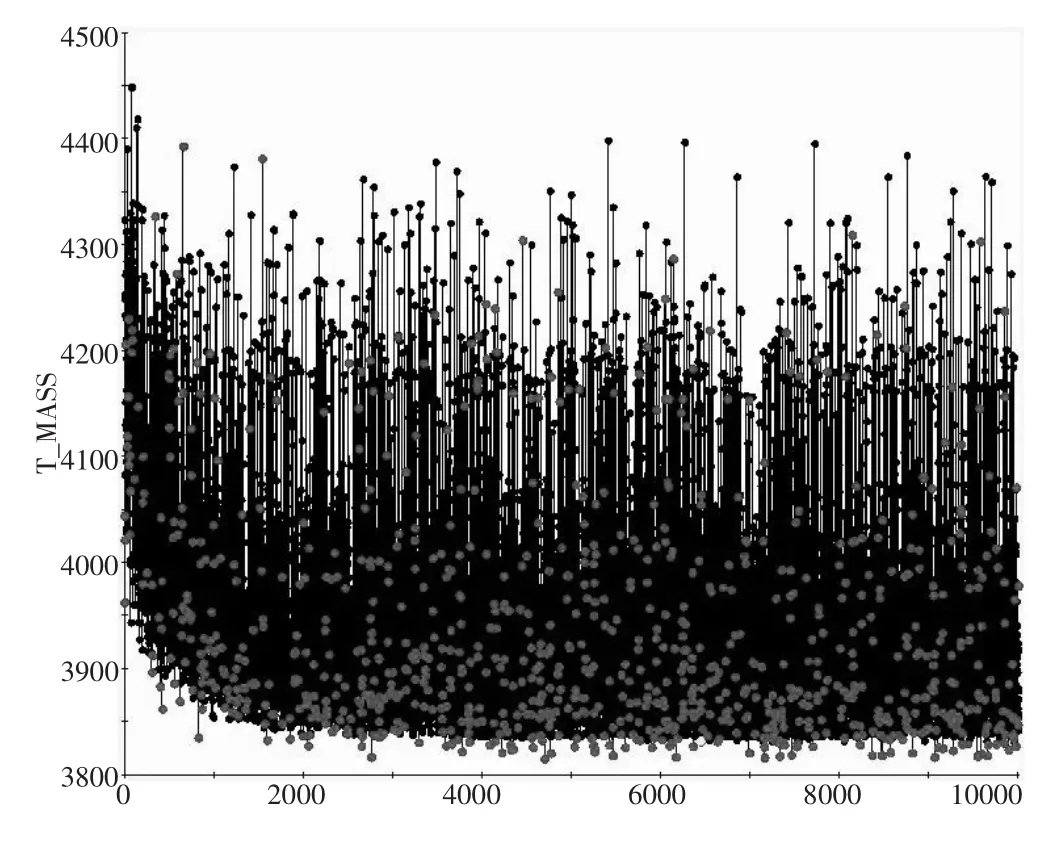
图4 T型架目标函数寻优历程

考虑到工程实际中，钢材的厚度与结构尺寸为离散整数，故对设计变量进行离散处理，优化前后的结果如表3所示。

表3 T型架初始值与优化值对比

由表3可知，相比于初始值，优化后模型的各设计参数均有所减小，而静刚度与等效应力值均增大，但均在许用范围之内，且T型架自重有明显下降。

为了验证响应面近似模型优化设计的精度，将各设计变量的优化值代入T型架有限元模型，得到有限元分析结果如图5和图6所示。

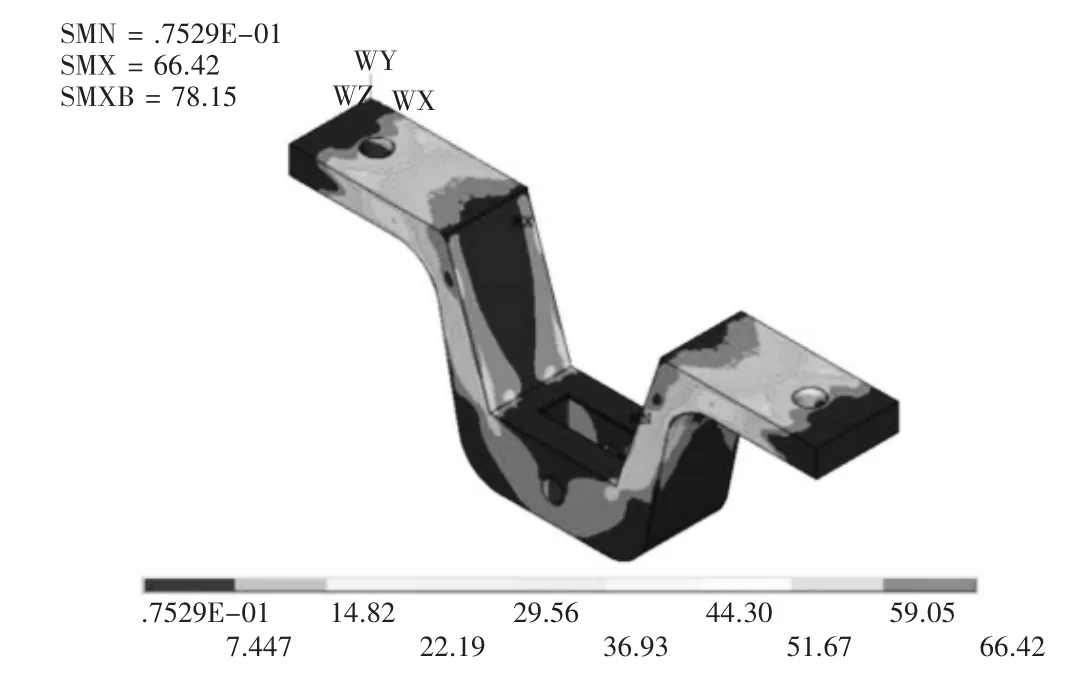
图5 优化后T型架等效应力图

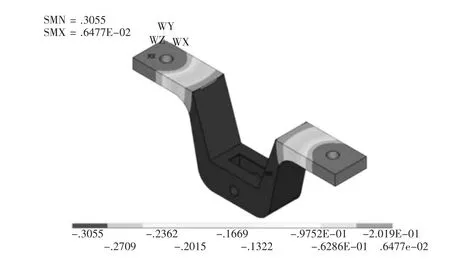
图6 优化后T型架位移等值线图

由图5与图6可知，T型架的最大等效应力为66.42 MPa，垂直方向最大静刚度为0.305 5 mm，均小于许用值，与近似模型优化结果相比，误差分别为4.04%，3.59%，误差较小，故此近似模型可以代替有限元模型。

优化设计后，T型架结构自重减轻了108.58 kg，较原结构减轻了36.12%，优化效果较为明显。

4 结束语

（1）采用ISIGHT平台中最优拉丁超立方设计方法生成设计变量初始点，再通过调用ANSYS软件完成进而构建响应面近似模型，减少了计算量。

（2）利用多岛遗传算法对T型架响应面近似模型进行优化，该方法能极大提高优化效率，同时使T型架结构自重降低36.12%，对T型架的设计具有重要指导作用。