硬币材料特征峰幅度的探究
熊俊林,王春梅,沈国土
(华东师范大学 物理与材料科学学院,上海 200241)
X射线实验[1-4]内容之一为探究硬币的金属种类,先对FeZn标准样品的特征谱进行测量并对能量进行定标,然后通过测量1元/5角硬币的特征峰确认构成的金属. 在测量Fe和Zn的Kα特征峰时,“将入射角和出射角耦合设为45°”这一条件引起了一系列问题探究:为什么入射角和出射角要相同?为什么要选择45°?X射线一次激发产生的X射线是否是各向同性的?X射线实验仪是分析实验室的重要工具,也是本科生能熟练使用的仪器. 本文利用德国莱宝教具公司生产的X射线实验仪X-ray apparatus(554800)对单元素金属及多元素合金次级X射线Kα特征峰峰值随入射角及出射角的变化关系进行了探究,并从理论上对单元素金属进行了数据拟合.
1 实验原理
1.1 X射线的一次激发
波长为λ的单色原级X射线平行光束,如图1所示,以入射角ψ1入射到均匀样品表面上的强度为Iλ,经过样品深度为x,并在厚度为dx的薄层上激发了原子发出次级X射线,由小体积ΔV处原子发射出的次级X射线与样品表面的夹角为出射角ψ2.
若原级X射线被样品全部吸收,并令
得到质量比为Ci[5]的i元素的X射线荧光进入准直器的部分为[6-7]
(1)
式中,Pi,λ是出射的次级X射线强度,μs,λ是样品对波长为λ的入射X射线的质量吸收系数,Ei=Jifiωi,其中Ji,fi和ωi分别表示i元素相应的吸收限跃迁因子、谱线分数和荧光产额,这3个量只与元素种类有关.
对于多色X射线的激发,在计算一次荧光强度时需要在小于待测元素所测量谱线对应的吸收限λabs,i的波长范围内予以积分或求和,即i元素一次荧光强度的理论计算公式为
(2)
可以将之转换到原级能量谱进行积分求和计算.
1.2 X射线的二次激发
由于Zn的Kα和Kβ线波长(0.143 7 nm和0.129 6 nm)均小于Fe的Kα系吸收限(0.174 3 nm),因此均可激发Fe的K系特征谱线,即为X射线二次荧光激发. 同理,由于Fe的Kα和Kβ线波长(0.193 7 nm和0.175 7 nm)均大于Zn的K系吸收限(0.128 3 nm),故Zn的K系特征谱线不会被Fe激发,为一次激发.
对于FeZn合金体系,考虑Zn Kα及Zn Kβ对Fe激发而产生的二次荧光,则Fe的二次荧光产生的物理过程经猜测如图2所示,波长为λ的入射X射线Iλ到达dx1处被样品吸收,并且在dx1处激发Zn产生Zn Kα线和Zn Kβ线,Zn Kα线和Zn Kβ线到达dx2处被样品吸收,并在dx2处激发Fe产生Fe Kα线.
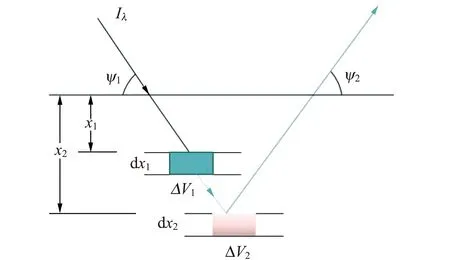
图2 二次X荧光示意图
本实验所用的FeZn合金片中Fe的质量分数为79.55%,该值可由测量FeZn合金片的体积和质量得到.
2 实验内容
为了探究原级X射线的入射角以及出射角对于次级X射线的特征峰峰值的影响,实验中分别对1元硬币(Ni)、5角硬币(Cu)及FeZn标准样品进行了测试.
分别将FeZn标准样品、1元硬币以及5角硬币固定在靶台上,然后运行德国莱宝教具公司开发的软件CASSY Lab,设置X光管的高压U=35.0 kV,电流I=1.00 mA,测量时间Δt=100 s. 靶台和传感器的角位置如图3所示.
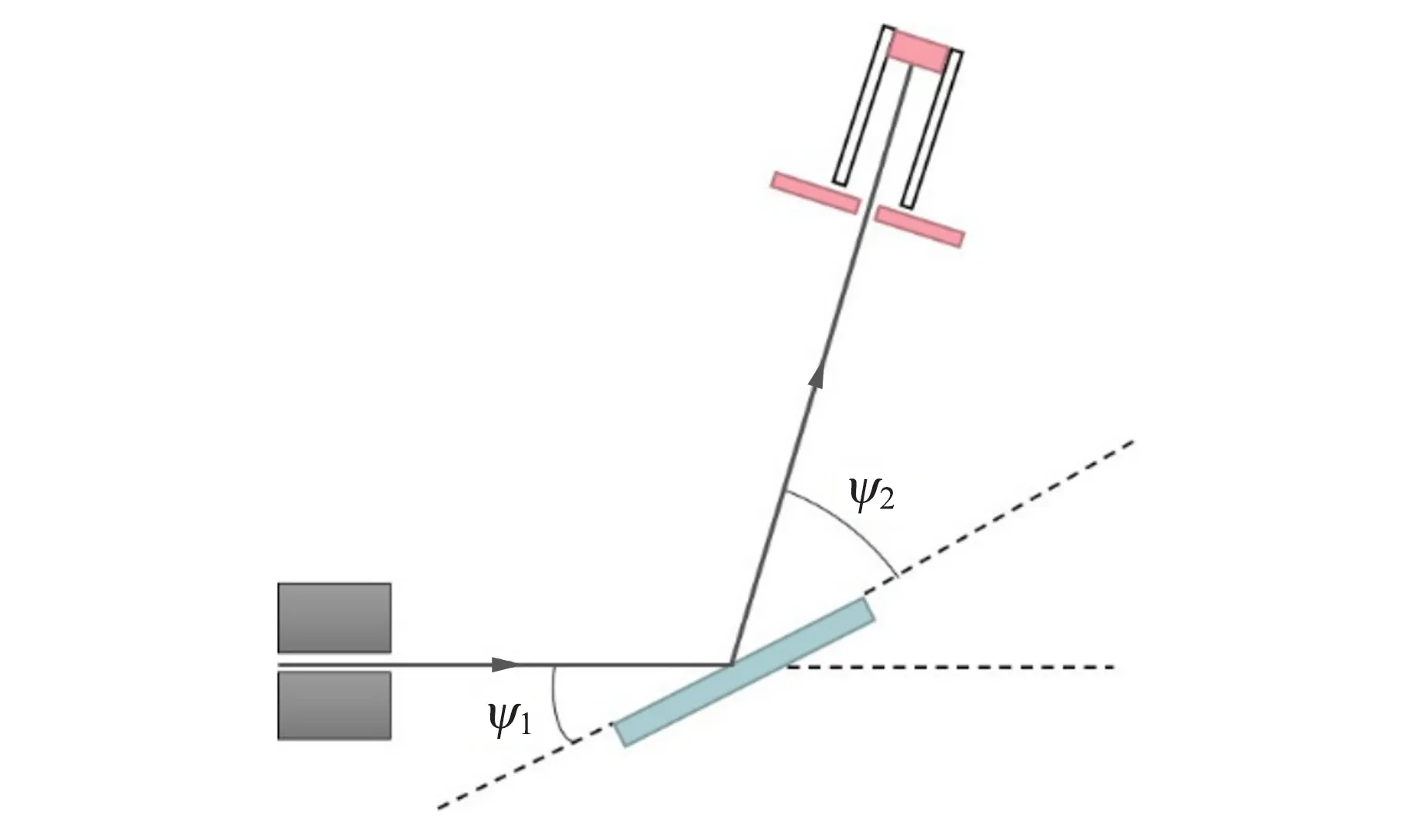
图3 靶台和传感器的角位置
首先将入射角与出射角耦合(COUPLED模式即保持入射角等于出射角),从10°到45°每隔5°改变入射角得到一系列特征峰峰值随入射角角度变化的数据. 再将入射角保持不变(SENSOR模式),从5°到45°每隔5°改变出射角得到一系列特征峰峰值随出射角角度变化的数据,进而定量验证一次激发理论的正确性及定性探究二次激发理论的可靠性.
3 实验结果与分析
3.1 原级X射线的光谱
为得知每个波长对应的能量Iλ,先测试原级X射线(Mo靶)的光谱,如图4所示.
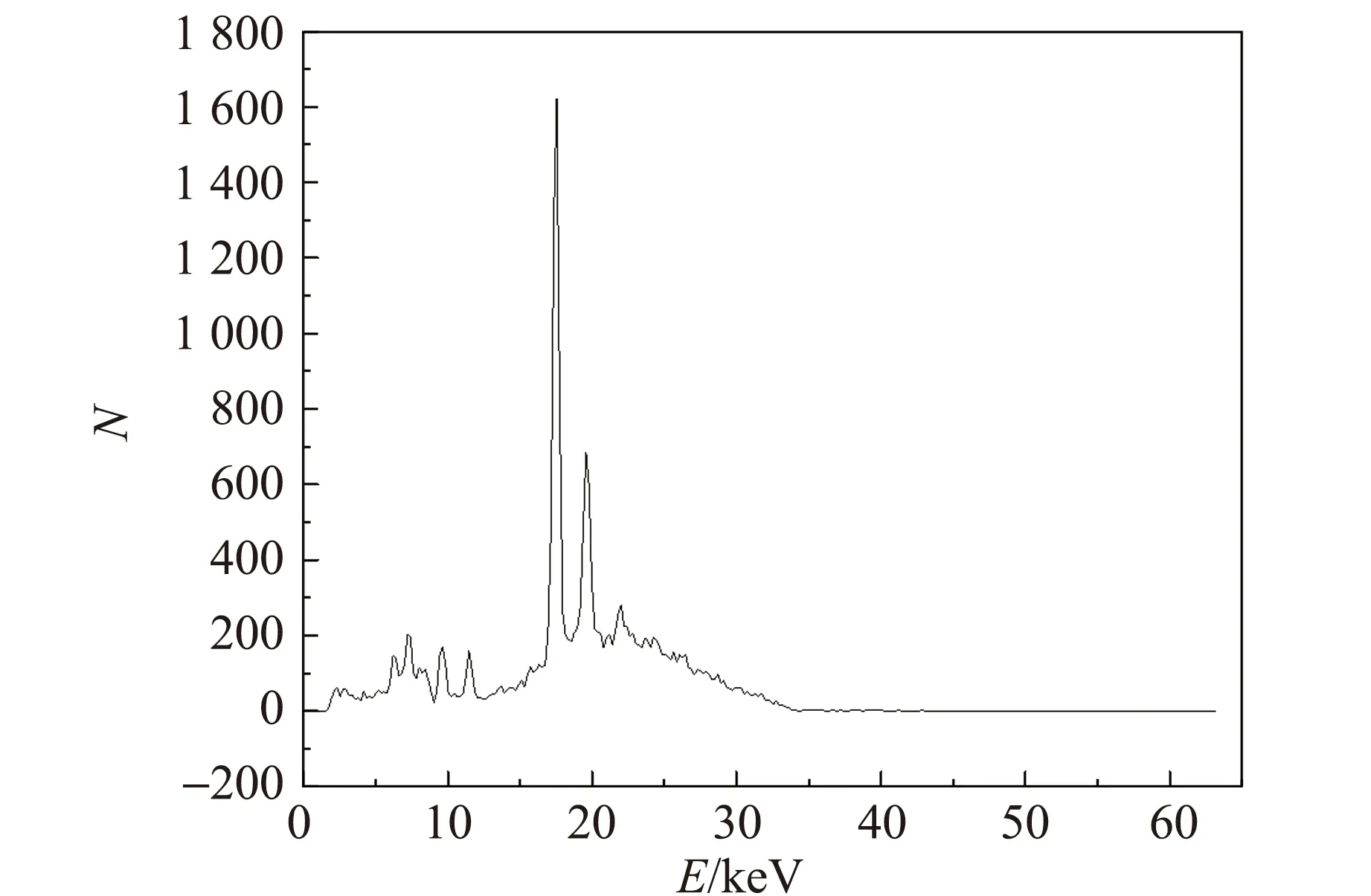
图4 Mo靶的原级X射线谱
同时,由布拉格-皮尔斯定律[8]和文献[5]中数据进行比较,可以得出K=0.211 348 cm2/(g·nm3),进而求得相应元素对于相应波长的质量吸收系数.
查阅文献[7-8],得到Cu,Zn,Fe以及Ni元素相应的吸收限跃迁因子Ji、谱线分数(即Kα跃迁概率)fi和荧光产额ωi等信息,如表1所示.
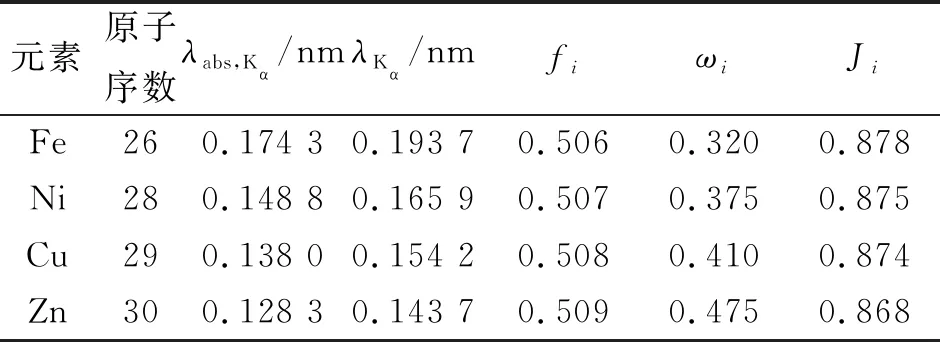
表1 Cu,Zn,Fe以及Ni元素相应的参量
3.2 单元素的次级X射线
图5为入射角和出射角耦合时的单元素金属的次级X射线Kα特征峰峰值随入射角的变化情况.
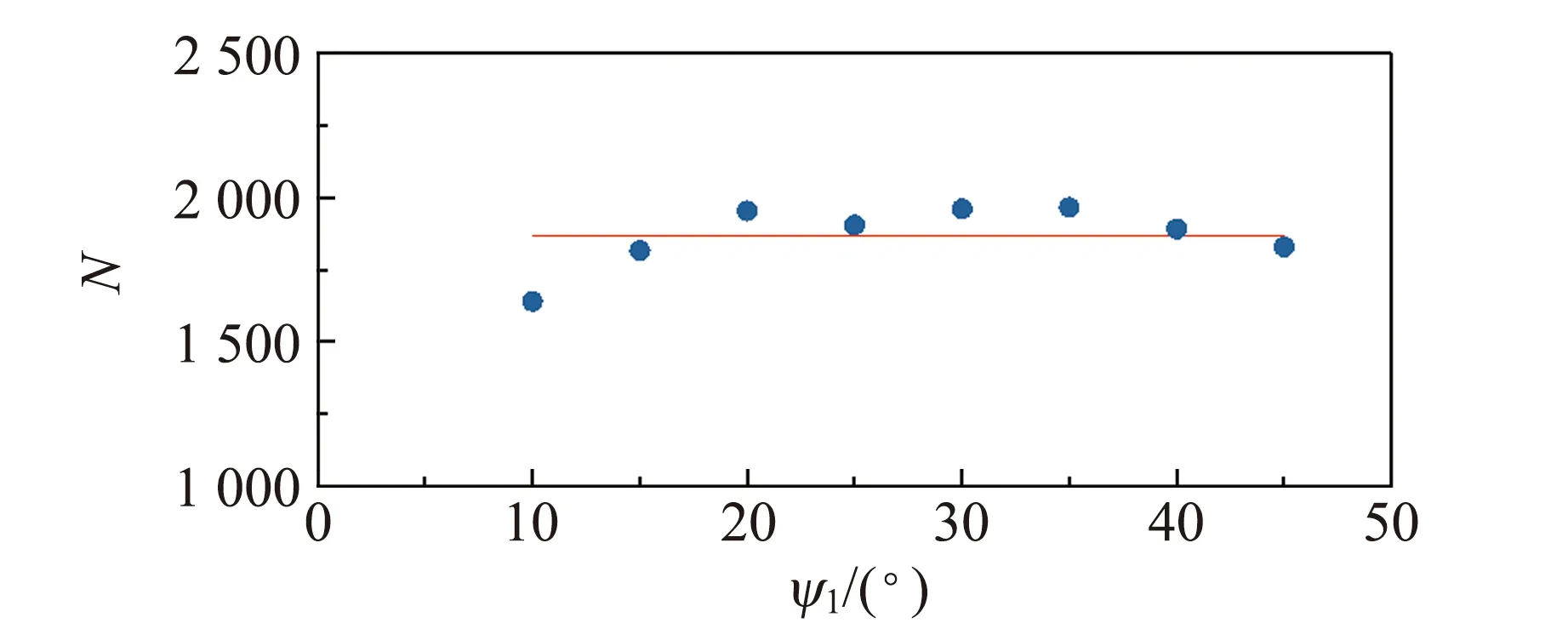
(a) 5角硬币
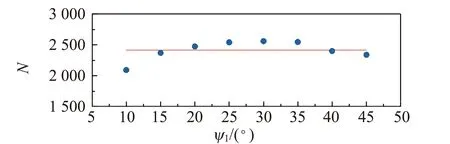
(b) 1元硬币图5 入射角和出射角耦合时的单元素金属的次级X射线Kα特征峰峰值随入射角的变化
图6为入射角保持20°不变,改变出射角时的单元素金属的次级X射线Kα特征峰峰值随出射角的变化情况.
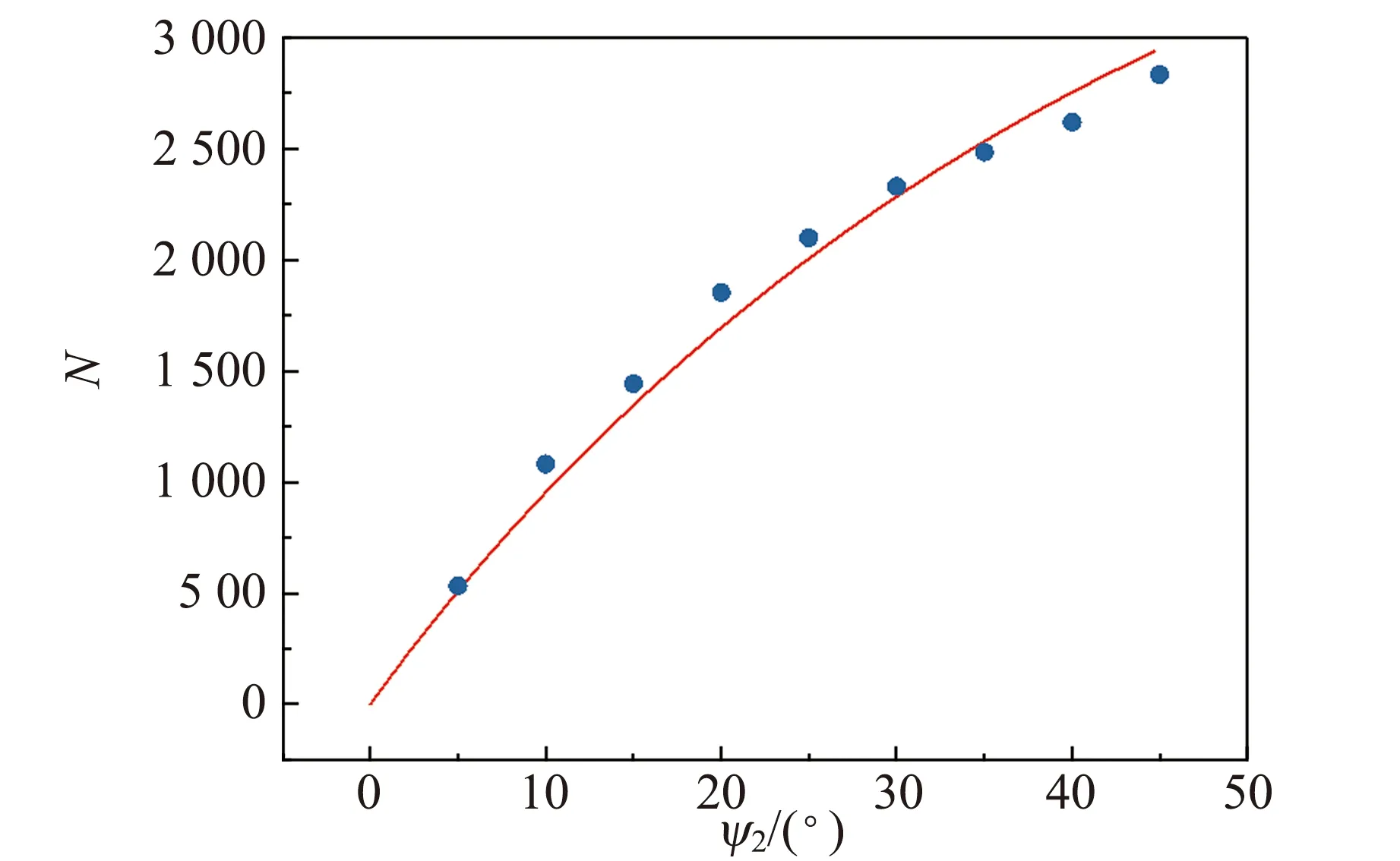
(a)5角硬币

(b) 1元硬币图6 入射角保持20°不变,单元素金属的次级X射线Kα特征峰峰值随出射角的变化
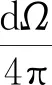
3.3 FeZn合金片的次级X射线
图7为入射角和出射角耦合时的FeZn合金片的次级X射线特征峰峰值随入射角的变化情况. 图8为入射角保持20°不变,改变出射角时的FeZn合金片的次级X射线特征峰峰值随出射角的变化.

(a) Fe

(b) Zn图7 入射角和出射角耦合时的FeZn合金的次级X射线Kα特征峰峰值随入射角的变化

(a) Fe
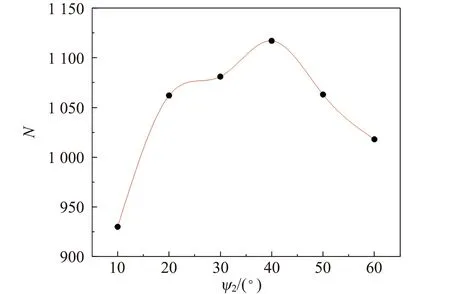
(b) Zn图8 入射角保持20°不变, FeZn合金的次级X射线Kα特征峰峰值随出射角的变化
对于FeZn合金体系,考虑Zn Kα及Zn Kβ对Fe激发而产生的二次荧光,根据参考文献[6],Zn对Fe的二次激发产生的荧光强度是随着出射角和入射角的增加而增加的. 当入射角与出射角相同时,Fe和Zn的一次激发荧光射线特征峰峰值不随角度的改变而改变,但Zn对Fe的二次激发随入射角的增大而增大,即Fe的总的X射线荧光强度随出射角的增大而增大,Zn的总的X射线荧光强度的损失量(对Fe的二次激发)随出射角的增大而增大,也即Zn的总的X射线荧光强度随出射角的增大而减小;当入射角不变时,Fe和Zn的一次激发荧光射线Kα特征峰峰值随出射角的增大而增大,但同样因为Zn对Fe的二次激发随入射角的增大而增大,Fe的总的X射线荧光强度随出射角的增大而增大,而Zn的总的X射线荧光强度随出射角的增大呈现先增加后减小的趋势. 理论与实际测量数据点定性符合,验证了X射线二次荧光激发的理论.
4 结束语
利用X射线实验仪测量了不同模式下单元素金属及多元素合金次级X射线特征峰峰值随入射角及出射角的变化,并且基于数据及理论分析了次级X射线特征峰峰值与角度的依赖关系. 目前X射线Kα光谱分析技术已被广泛应用于冶金[9]、地质[10]、矿物[11]、生物[12]、医疗[13]、刑侦、考古[14]等诸多领域. X射线光谱分析已成为物质组成分析的必备方法. 本实验充分利用实验室的资源,使学生开拓了思路,提高了其动手能力,同时帮助学生了解了X射线的产生与激发的过程,进一步掌握X射线光谱分析技术的原理.

