考虑碰撞工况的电动汽车电池箱多目标拓扑优化设计

袁 林，赵清海,2，张洪信，付 磊，王文玥

0 引言

随着环境污染和石油资源的短缺，节能减排是汽车工业技术发展的必然选择，而发展电动汽车已成为当前汽车行业发展的总体趋势，对于电动汽车电池箱的研究也越来越受到关注。电池箱作为电池的主要承载装置，在保证电动汽车电池箱碰撞安全性的同时，进行轻量化设计，对降低电动汽车整车的重量，改善电动汽车续航里程的性能有重要的意义。近年来，电池箱碰撞安全性领域的研究受到广泛的关注。文献[1]通过采用Solidworks Simulation对公交大巴电池箱进行仿真分析，验证公交大巴电池箱在多变的路况下，是否满足电池箱对锂电池的保护性能。文献[2]借助线性疲劳累计损伤理论与材料S-N曲线对电动汽车电池箱结构进行随机振动疲劳分析，使其结构设计满足疲劳寿命的要求。文献[3]根据电池包箱体及内部结构碰撞响应分析方法，对电池包内部结构在碰撞过程中的变形及响应进行研究，为电池包设计开发、性能分析以及安全评价提供参考。

基于此，本文将多目标拓扑优化的方法引入到考虑碰撞工况下的电池箱结构设计中。通过在HyperMesh的LS-DYNA接口中，建立电池箱正面碰撞、后面碰撞、左右侧面碰撞工况的有限元模型，使用LS-DYNA求解器对该模型进行有限元求解，将碰撞工况的求解分析结果刚性墙反力作为等效静载荷[4]施加到拓扑优化中，借助于HyperWorks软件中的0ptistruct模块，通过层次分析法确定正面碰撞、后面碰撞、左右侧面碰撞工况的权重，采用带权重的折衷规划法和平均特征值法，建立静态多工况刚度拓扑优化模型和动态特征值拓扑优化模型。将电池箱的多目标函数最优解问题转化为单目标函数最优解问题，从而得到同时满足多工况下刚度最大和低阶频率最高的电池箱结构，最后对电池箱进行碰撞验证优化效果。通过优化实现了电池箱的轻量化设计，同时又满足了电池箱碰撞工况下的安全性。

1 电池箱碰撞工况

1.1 电池箱有限元模型的建立

本文以某电动汽车电池箱为研究对象，电池箱的三维简化图，如图1所示，图中电池箱由上下箱体和托架构成电池箱的基本结构，电池箱建模尺寸：长是2000mm，宽是1500m，高是300mm，上下箱体的厚度为4mm，托脚厚度为2mm。将三维模型导入HyperMesh软件，为不影响求解精度，对模型进行几何清理，选取壳单元对电池箱三维简化图进行网格划分，有限元模型总质量为124kg，包括39619个节点，39630个单元。电池箱的有限元模型如图2所示。

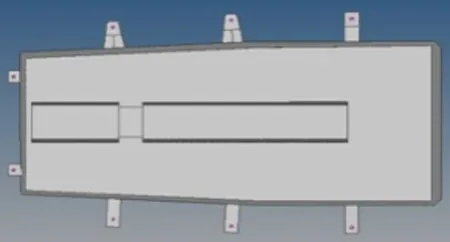
图1 电池箱三维简化图

图2 电池箱有限元模型

在材料模型的选取上，本电池箱下箱体和上箱体采用的材料为低碳冲压钢DC01，托架采用的材料为普通碳素结构钢Q235，参照机械工程材料手册[5]，列出了DC01与Q235的材料参数取值，如表1所示。

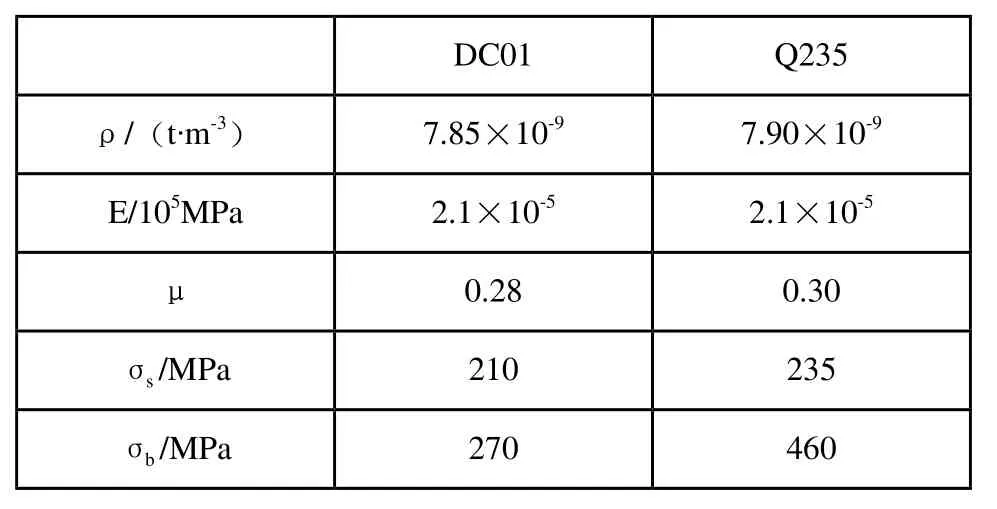
表1 DC01和Q235材料力学特性

根据上下箱体和托架的材料的选用，同时考虑到碰撞工况，在碰撞工况有限元建模中选用MAT24的材料模型。

1.2 碰撞仿真模型的建立

本文利用HyperMesh的LS-DYNA接口，建立电池箱碰撞仿真模型。在电池箱碰撞仿真建模中，电池箱碰撞的刚性壁障一般简化为刚性墙[6]，刚性墙的创立通过Analysis页面rigid walls菜单实现。在电池箱碰撞工况中，还需要对电池箱施加初始速度，设定此模型正面碰撞的初始速度为4000mm/s的低速碰撞，同时设置仿真时间为100ms。如图3所示，依次建立电池箱正面碰撞、追尾、左右侧面碰撞工况的仿真模型。

图3 碰撞工况模型

1.3 碰撞工况的仿真与分析

利用hypermesh完成全部前处理后，将文件输出提交给求解器求解。本文使用LS-Dyna软件作为求解器，将hypermesh中的碰撞模型以k文件的形式输出，然后将k文件提交给LS-Dyna进行求解计算。LS-Dyna求解完成后，将结果文件Glstat和RWforce导入到hypergraph中进行结果观察。

通过对碰撞仿真结果进行分析，正面碰撞能量曲线如图4(a)所示，在电池箱正面碰撞过程中，动能和时间呈非线性的关系逐渐减少，在初始时刻，动能最大，随着碰撞的开始，电池箱开始发生变形吸收碰撞的能量，动能逐渐减少，内能逐渐增加，其余的转化为热能等消耗掉，整个过程，动能和内能的变化趋势相反，符合能量守恒定律，且系统沙漏能一直保持在3%左右，对沙漏的控制[7]是成功的，从而验证了仿真计算的正确性。图4(b)、图4(c)、图4(d)分别为电池箱后面碰撞、左侧面碰撞和右侧面碰撞的能量曲线。

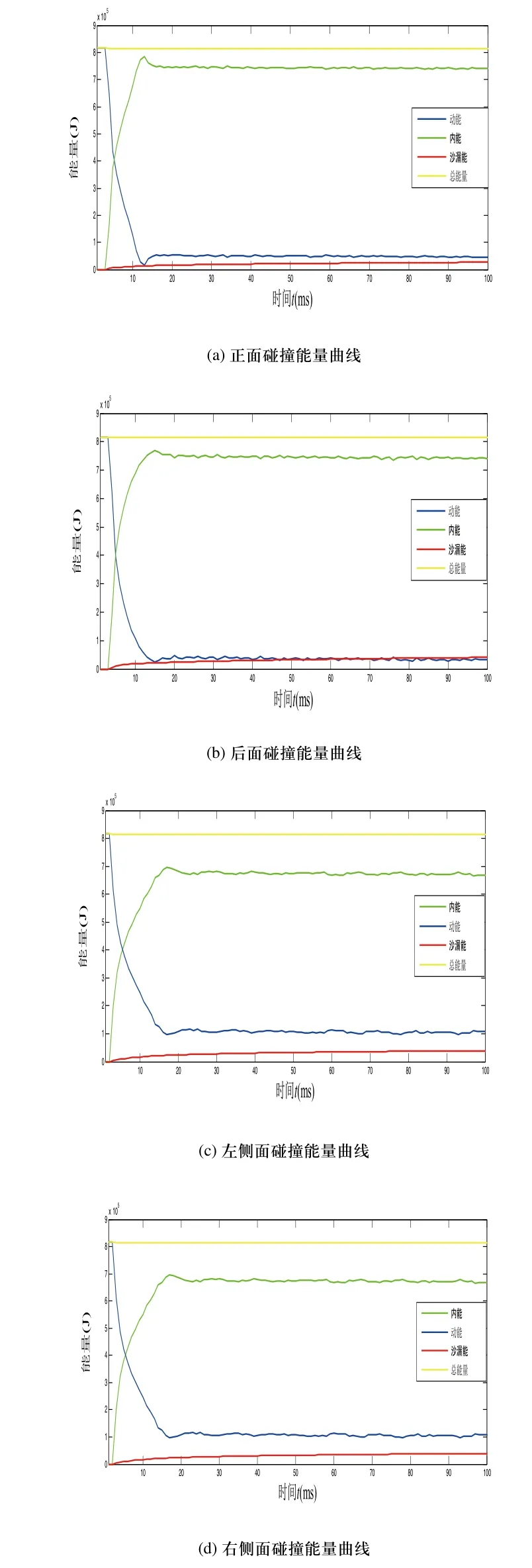
图4 各工况能量曲线

电池箱正面碰撞力曲线如图5(a)所示，在碰撞过程中，正面碰撞电池箱所受的最大刚性墙反力是91997N。如图5(b)、图5(c)、图5(d)所示，电池箱后面碰撞、左侧面碰撞和右侧面碰撞的最大刚性墙反力分别为120773N、88012N、74388N，作为电池箱多工况下的载荷，并以均布力的形式施加到电池箱。

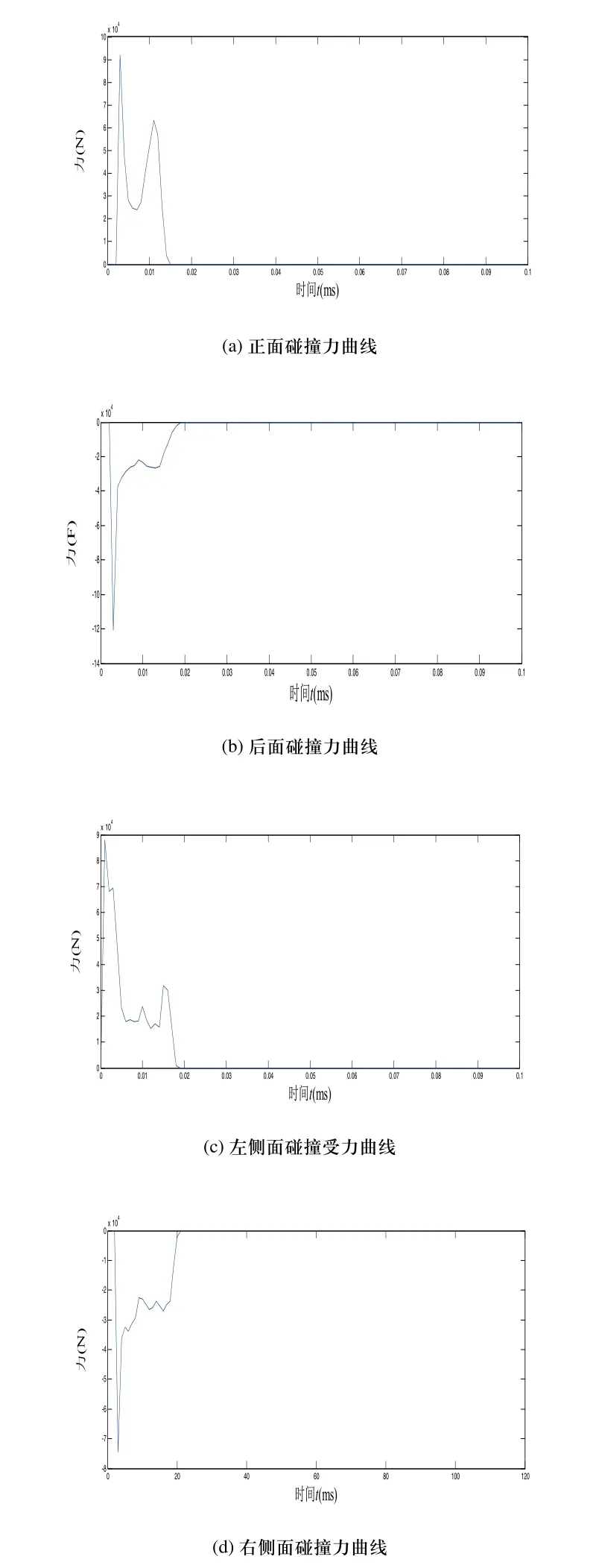
图5 各工况碰撞力

2 基于OptiStruct的电池箱多目标拓扑优化

2.1 电池箱拓扑优化模型的确定

使用HyperWorks软件中的0ptistruct模块，对电池箱进行拓扑优化。在进行拓扑优化前，对图2所示的电池箱有限元模型划分设计区域，上箱体和下箱体为设计区域，托架为电池箱的非设计区域。对电池箱施加边界约束（SPC），对每个电池箱托脚X、Y、Z三个方向的平动自由度进行约束，同时释放每个电池箱托脚的三个转动自由度。

2.2 静力学拓扑优化数学模型

进行静力学拓扑优化，本例中设计变量是电池箱的单元密度，约束条件是设计区域的体积分数，目标函数是柔度最小。采用层次分析法[8]和折衷规划法[9]定义电池箱平均柔度目标函数静态多工况拓扑优化数学模型为：

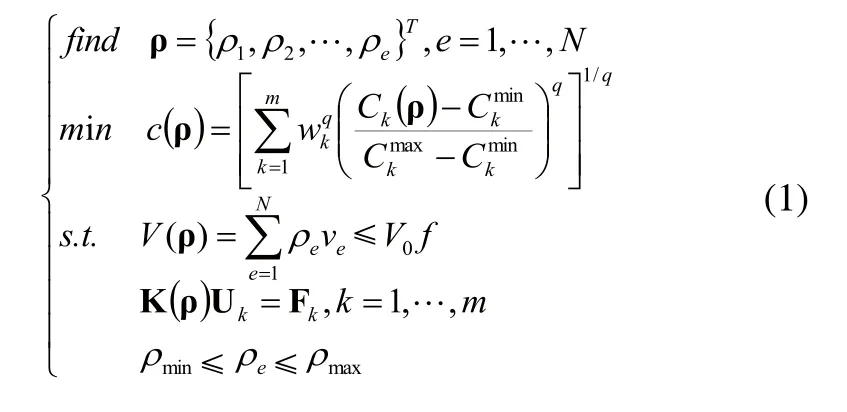
式中，ρ是单元的相对密度；N为设计区域总的节点数目；m为结构所受工况的数量；ck（ρ）是第k个工况的柔度值；Ckmax、Ckmin分别为第k个工况单独进行优化时柔度的最大值和最小值；q为惩罚因子，在本文中取q=2；ve为单元体积；V0与f分别为优化后的总体体积与结构体积分数约束；K是刚度矩阵，F是载荷矩阵，U是位移矩阵；wk为工况权系数，对于多工况载荷权值的确定，本文创新性的采用层次分析法来权衡各工况之间的相对重要程度，合理给出评价工况的权重系数。层次分析法的核心问题是创建一个合理且一致的判断矩阵，判断矩阵的合理性取决于标度的设置。标度是指设计人员对各个指标相对重要度等级差异的量化评价，一般应结合专家经验对标度进行设置。本文选取1～9标度法，其定义如表2所示。

表2 1～9标度法及其含义

通过两两比较工况间的相对重要度，进而构建判断矩阵，即：

式中，n为工况总数；aij表示第i工况对第j工况的相对重要度。本例中，电池箱静态柔度拓扑优化中考虑四种工况：前碰工况，后撞工况，左右侧碰，这四个工况按照层次分析法的主观判断如下：前碰工况的重要性最高，后碰工况和左侧碰撞工况的重要性也较高，右侧碰撞工况的重要性相对较低，进而设定四种载荷工况，n=4，并进行两两比较，构建判断矩阵：

计算得到：

因此，该矩阵满足一致性要求。计算得到前四阶特征值对应的权值系数wi（i=1，2，3，4）分别为0.5222、0.1998、0.1998、0.0782。即正面碰撞权系数为0.5222，后碰和右侧面配置的权系数为0.1998，右碰工况权系数为0.0782。

2.3 动力学拓扑优化数学模型

进行动力学拓扑优化，本例中设计变量是电池箱的单元密度，约束条件是设计区域的体积分数，目标函数是低阶频率最大化。采用平均特征值法[10]定义其优化数学模型为：

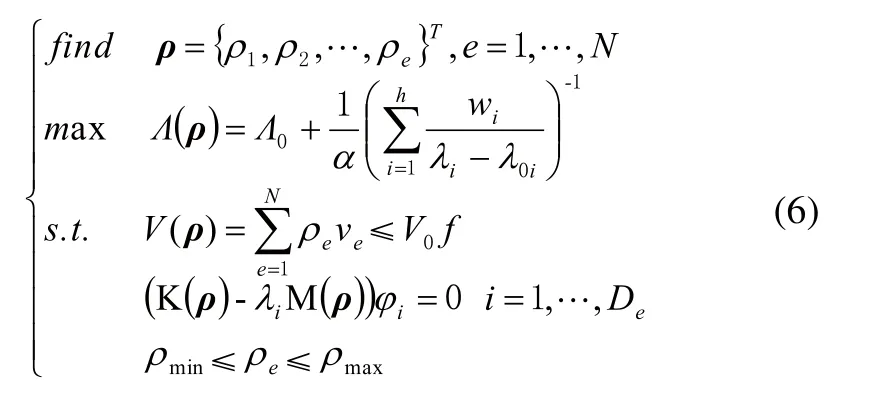
式中，ρ是单元的相对密度；N为设计区域总的节点数目；Λ(ρ)为平均特征值，h为电池箱优化的频率阶次；λi为第i阶特征值；λ0i与α为给定参数；wi为第i阶特征值的权系数；M为质量矩阵；De为设计区域有限元模型的总自由度数[11]。

2.4 多目标拓扑优化数学模型

基于折衷规划法的静态多工况和动态多阶固有频率的拓扑优化数学模型：

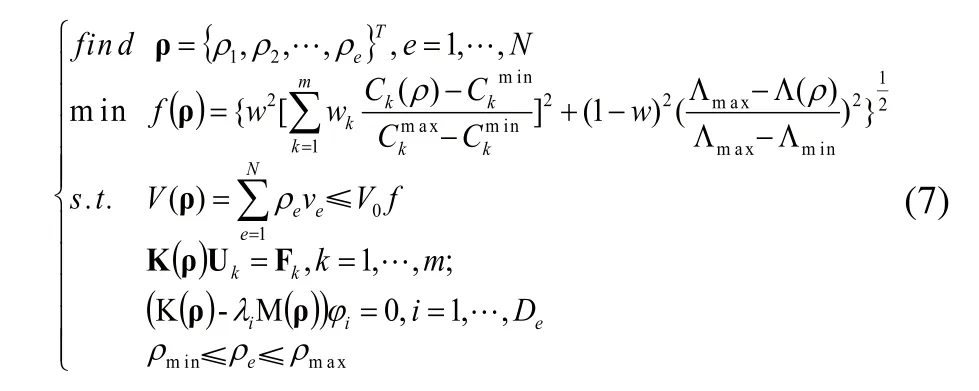
式中，ρ是单元密度；w为权系数，取值区间为[0,1]；m是工况数；Ckmax、Ckmin是第k个工况柔度的最大值和最小值；Λmin、Λmax是平均特征值的最大值和最小值。ρmin、ρmax是单元密度的上限和下限，单元密度取值区间数[12]为[0,1]。

2.5 拓扑优化结果

通过优化，电池箱多目标拓扑优化结果如表3所示，由表可知，当w=0.4时获得最优妥协解[13]，当权系数为0.4时，电池箱上下箱体静态和动态多目标拓扑优化结果如图6所示。

2.6 电池箱结构改进

根据上述拓扑优化的结果，对电池箱结构进行改进设计。由图6可以看出，红蓝分布比较明显，说明较好的控制了离散度。对于上箱体在建模中，蓝色区域的厚度仍为4mm，灰色区域厚度为1mm。对于下箱体在建模中，蓝色区域厚度同校为4mm，添加承重梁厚度为1mm。优化后电池箱有限元模型总质量为91kg，与优化前124kg相比，质量减轻26.6%，改进的电池箱模型如图7所示。

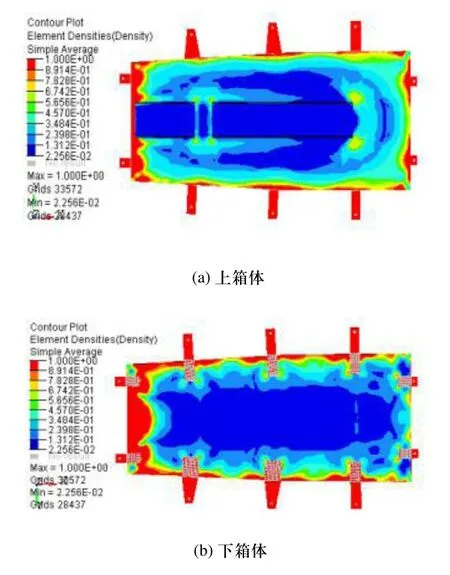
图6 静态和动态多目标拓扑优化结果（w=0.4）

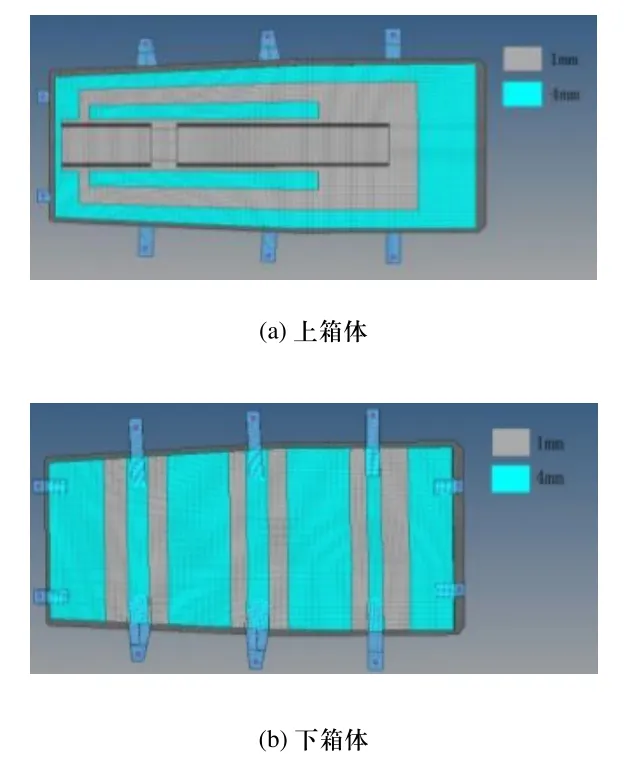
图7 改进的电池箱

3 电池箱性能验证

3.1 电池箱静强度验证

对拓扑优化后的电池箱进行静强度验证，以优化后的应力和位移作为验证的性能指标[14]。四个工况的优化前后静力学性能对比如表4所示。通过分析四种工况下电池箱表面应力值和变形情况可以得到，电池箱最危险的工况是后碰工况，其最大应力小于材料的屈服应力[15]210MPa，与材料的屈服强度相比，电池箱优化设计后满足强度设计要求。后碰工况的应力云图和变形云图如图8所示。

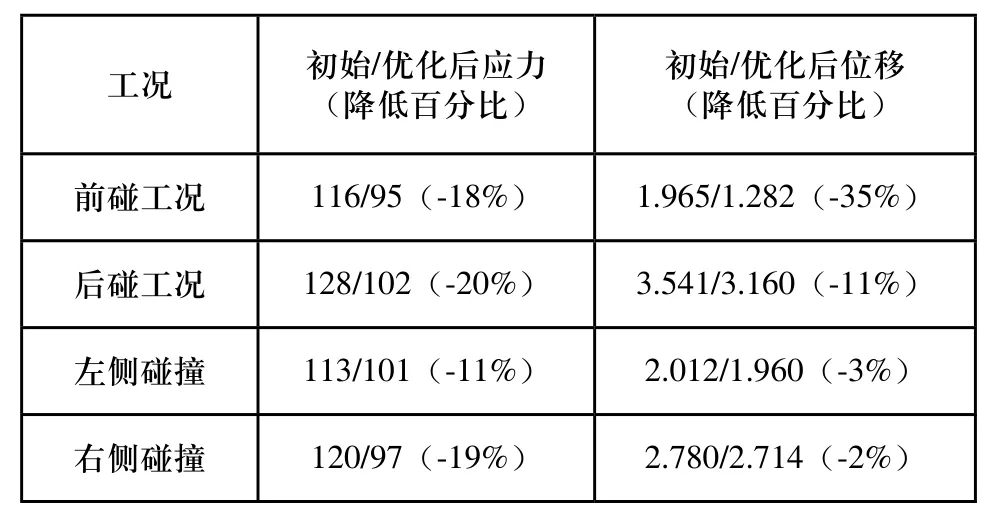
表4 电池箱各工况应力、位移对比

图8 优化后结构后碰工况

3.2 电池箱模态验证

拓扑优化前电池箱结构一阶固有频率为19.47Hz，拓扑优化后电池箱一阶固有频率为28.67Hz，与优化前先比增加了9.2Hz，超过电动汽车动力系统要求的最低25Hz的要求，满足设计要求，电池箱第一阶模态阵型如图9所示。

4 结论

本文对电动汽车电池箱进行正面碰撞、后面碰撞、左右侧面碰撞工况的仿真分析，从能量的角度，验证碰撞工况仿真的正确性，并将仿真计算结果应用到拓扑优化中。基于拓扑优化的理论，详细阐述了静态多工况拓扑优化，动态特征值拓扑优化和静动态多目标拓扑优化，通过优化的结果，对电池箱进行优化设计，最后对电池箱进行性能验证。结果表明，本文提出的研究方法，既满足了电池箱碰撞的安全性，同时又降低了电池箱本身重量，为电池箱在结构上的安全设计提供了参考依据，具有一定的实际应用价值。

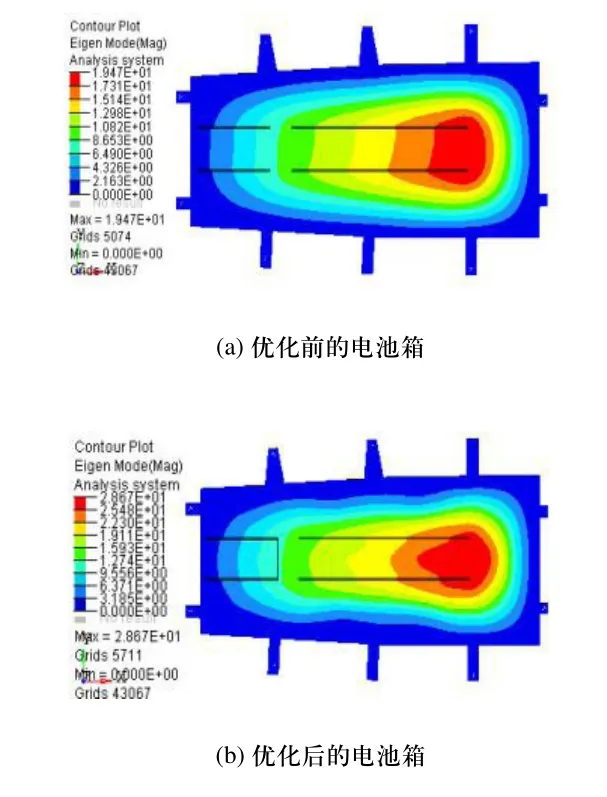
图9 电池箱第一阶模态阵型