基于改进蚁群算法的逆向物流车辆路径优化

陈秀娟，高更君，冯媛媛

（上海海事大学 物流研究中心，上海 201306）

0 引言

在提倡节约型社会，大力发展循环经济的趋势下，供应链闭环管理视角下的逆向物流得到了国内外业界专家的普遍重视。逆向物流车辆路径问题（Vehicle routing problem in reverse logistics，VRPRL）是派车和路径优化的整合，一直以来都是逆向物流领域中的热点问题，研究如何优化逆向物流车辆路径具有重要的理论及经济意义。

目前很多学者对路径优化问题已有一定深入研究，例如，Thibaut Vidal等[1]用一种混合遗传算法解决带时间窗的VRP问题；Chao[2]利用禁忌搜索算法求解了多车型的VRP问题；刘志硕等[3]提出基于可行解两阶段构造策略的自适应蚁群算法求解VRP问题。这些启发式算法在解决车辆路径问题上都取得了一定成果，但也有不足，例如遗传算法可行解质量一般，禁忌搜索算法过于依赖初始解。蚁群算法凭借其鲁棒性和搜索较好解强的特点在解决车辆路径问题方面备受青睐，但蚁群在解决大规模问题时，也有一定局限性。对此，很多学者在逆向物流车辆路径优化中对基本蚁群算法进行了改进。刘艳秋等[4]提出逆选择操作蚁群算法，对蚁群概率选择进行改进，考虑到物流节点间存在不可行路径的问题，但未涉及信息素更新方式和启发因子的改进；胡天军等[5]解决回程取货逆向物流车辆路径问题时，吸收外激素平滑思想，减少信息素各边差异性，有利于产生新的搜索路线，但频繁更新局部信息素的方式降低蚂蚁的收敛速度；于雷等[6]在信息素更新方面融合并行思想，扩大了解的范围，但启发因子的设置只考虑到局部，不利于整体寻优；陈迎欣等[7]提出混合改进蚁群信息素更新的策略，但更新方式非动态，忽略了迭代次数增多的影响。基于此，本文拟提出动态改进信息素更新方式和启发因子的新思路，两者同时分阶段进行，有机结合，再结合2-opt算法进行优化，以期更高效准确地解决逆向物流回收路径问题。

1 VRPRL问题描述

逆向物流是一种包含退货、维修、废弃处理、等流程的物流活动，主要分为退货逆向物流和回收逆向物流两大类。本文主要研究的是废旧产品通过再循环、再生产从而重新再利用的回收逆向物流。在这一物流系统中，客户向逆向物流中心（以下简称“回收中心”）发出大批回收订单，回收中心接收订单并根据各个客户点的回收量，合理规划路线，安排车辆到各个客户点回收物资，并返回回收中心。本文研究对象为一个回收中心，n个回收客户，m辆车。问题目标是在满足回收要求的前提下，合理调度车辆，最小化车辆总行程。回收基本示意图如图1所示。

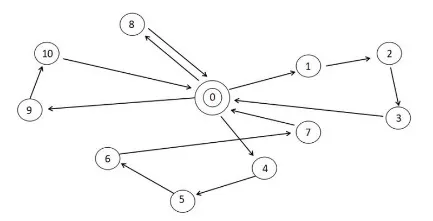
图1 回收示意图

2 VPRL模型建立

2.1 模型假设及参数设定

2.1.1 模型假设

1）回收中心和客户点坐标已知；

2）各客户点回收量已知，均不会超过一辆车的标准载容量；

3）每个客户点必须被且只能被一辆车服务一次；

4）回收货物类型相同；

5）路况对车辆的行驶距离没有影响；

6）回收中心的车辆型号相同，数量充足，每次回收任务行驶里程均不超过车辆最大行驶距离；

7）回收中心的容量足够大。

2.1.2 参数定义

0：配送中心；

Z：遍历所有客户行驶的总距离；

m：客户数量；

n：车辆数量；

dij：客户i,j之间的距离，dij=dji；

qi：客户i的回收量，q0=0；

Q：每辆车的最大装载量；

xijk：0-1变量，车辆k由客户vi出发后开向vj取值为1；否则取值为0；

yik：0-1变量，车辆k服务客户点i时取值为1；否则取值为0。

2.2 模型建立

根据上述VPRL问题描述，基于参数设定和模型假设，构建VRPL模型如下：

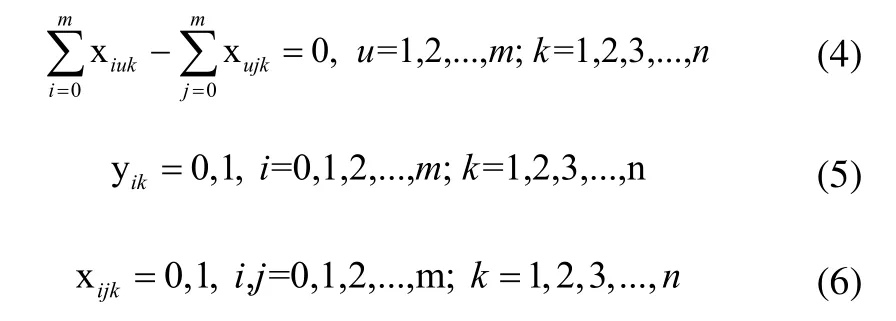
上式中，式(1)式为目标函数，求最小化行程；式(2)表示车辆载重约束，每个客户点的回收量都不能超过车的标准载容量；式(3)保证每个客户有且仅有一辆车为之服务；式(4)保证每辆车服务完某客户点后必须离开；式(5)和式(6)是变量取值。

3 模型求解

自然界中蚂蚁的初始运动是随机的，他们通过感知彼此释放的信息素浓度进行交流，并根据浓度大小选择下一步的运动方向，浓度越高表示距离越短，最后在正反馈作用下蚂蚁总能找到从蚁穴到食物源的最短路径。蚁群算法凭借其寻找较优解能力强和稳健性优的特点在优化车辆路径问题方面颇有优势，但蚁群在求解大规模问题时计算效率不高，容易陷入局部最优，针对其不足，本文对基本蚁群算法做一些改进。

3.1 改进蚁群算法

采用“可行解先行策略”，每只蚂蚁都遍历所有点，均构造一个可行解，在保证解空间存在及丰富的情况下，对信息素更新策略和启发因子进行动态改进，再对较优解利用2-opt算法优化，以期提高蚂蚁搜索质量，避免陷入局部最优。

3.1.1 改进信息素更新策略

基于文献[8]混合策略“实时更新和全局更新”的启发，本文考虑到蚁群迭代次数对算法的收敛性起重要作用，只将第10次作为实时更新和局部更新的切换点，不能更好得研究迭代次数更新的影响。本文将两者“动态”结合，20次一循环，前10次循环，区别于文献[8]选取本次循环中最优的可行解，均采用本次循环中所有蚂蚁搜索回路中的最短回路进行信息素更新，更好地引导蚂蚁进入优质循环中，找到更多可行解；后10次循环时，可以提高收敛速度，找出蚂蚁循环以来的最短的可行解进行信息素的更新，对最优解进一步搜索。这种局部与全局更新动态结合的策略，很大程度上避免了算法收敛过慢以及陷入较差解的情况。

信息素更新规则如下：

其中：

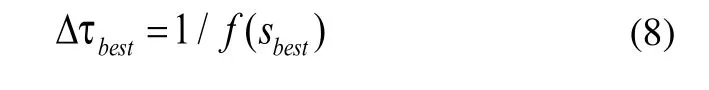
f(Sbest)表现本次迭代的最短回路Sib或者全局最优解Sob。

借鉴MIN-MAX思想，将各路径上的信息素浓度限定在某固定的范围内，减少浓度差距，避免算法陷入局部最优。

信息素更新前：

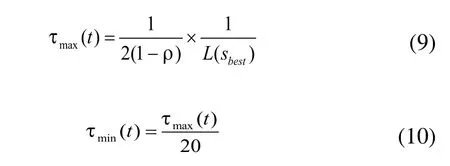
信息素更新后：

其中，L(Sbest)表示全局最优解或本次迭代最短回路，1/L(Sbest)表示每次迭代路径上新增的信息素最高值。

3.1.2 改进启发因子

启发函数的作用是帮助蚂蚁以更大的概率选择较短路径。目前大多文献采用以下三种方法：一种仅考虑局部因素（两点间距离）；第二种仅从全局最优解出发（配送中心和下一个目标城市距离）；第三种是将局部和全局结合起来考虑。前两种方法都有局限性，第三种考虑比较全面，但是一开始限制因素太多，容易过早陷入局部最优解，不利于整体寻优。本文启发因子结合信息素更新规则，动态调整，20次一循环，前10次循环，启发函数设为：

其中dij为i、j之间的距离，这校利于扩大解空间，增强蚁群搜索能力；后10次循环，启发函数设为：

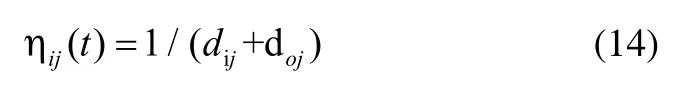
基于局部，定位全局，寻找最优解。

3.1.3 2-opt算法

2-opt算法是在蚁群算法求得的原始解基础上，交换所得解的两边，再将新解和原始解进行比较，新解更优则保留，反之舍弃。一直循环代替，直至完成。为减少工作量，降低算法效率，每只蚂蚁完成搜索后，将全部蚂蚁走过的路径长度按降序排列，对后1/2的路径利用2-opt算法优化。基本示意图如图2所示。

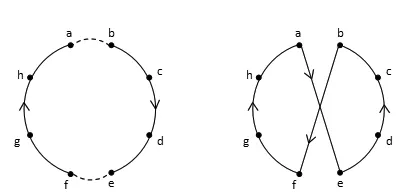
图2 2-opt示意图

3.2 算法步骤

根据改进蚁群算法，设计具体实现步骤如下：

1）从文件中导入回收中心和客户点的坐标等基础数据；

2）初始化蚁群各参数；

3）迭代次数nc=nc+1；

4）随机将m只蚂蚁放在n个城市上，初始化禁忌表tabuk和候选点集allowedk；

5）判断allowedk是否为空,若为空则跳到步骤10；否则判断allowedk表中剩余节点的回收量是否大于车辆的剩余载重量，假如车辆k的剩余载重量不能满足任何节点，则回到回收中心重新出发；假如存在满足的节点，则根据概率公式：

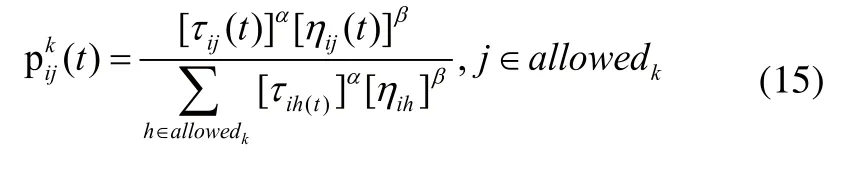
选择下一个客户点；

6）蚂蚁从i点出发到j点时，计算车辆k到客户点i后的剩余载重量；同时修改tabuk；

7）所有蚂蚁都找到一条包含所有节点的可行路径后，对路径长度进行降序排列，选取后1/2进行2-opt局部搜索，更新蚂蚁此次的最优路径长度和迄今为止最优路径；

8）计算Int（ncmax/20），若为奇数，则局部进行信息素更新；反之，按照全局信息素更新；

9）循环执行3）～8），判断循环次数是否超过ncmax,若不超过，则转步骤3）；若超过则跳转到步骤10）；

10）计算循环迭代ncmax后所得到的最短路径长度和最短路路径，得出算法结果并输出最优解路径，算法终止，输出最优路径长度。

根据此算法可通过Java语言编程求解得到车辆完成回收任务的最短行驶距离。

4 实例验证

为了方便比较和验证算法的有效性，本文采用文献[8]的逆向物流回收实例代入模型进行计算。该回收中心的车辆种类统一，车辆标准载容量为12t，回收中心与客户点，客户点与客户点之间的距离为两点间欧式距离，有1个回收中心和20个客户点，回收中心与客户点数据如表1所示。采用运行参数如下：M=60，α=1，β=2，ρ=0.5。

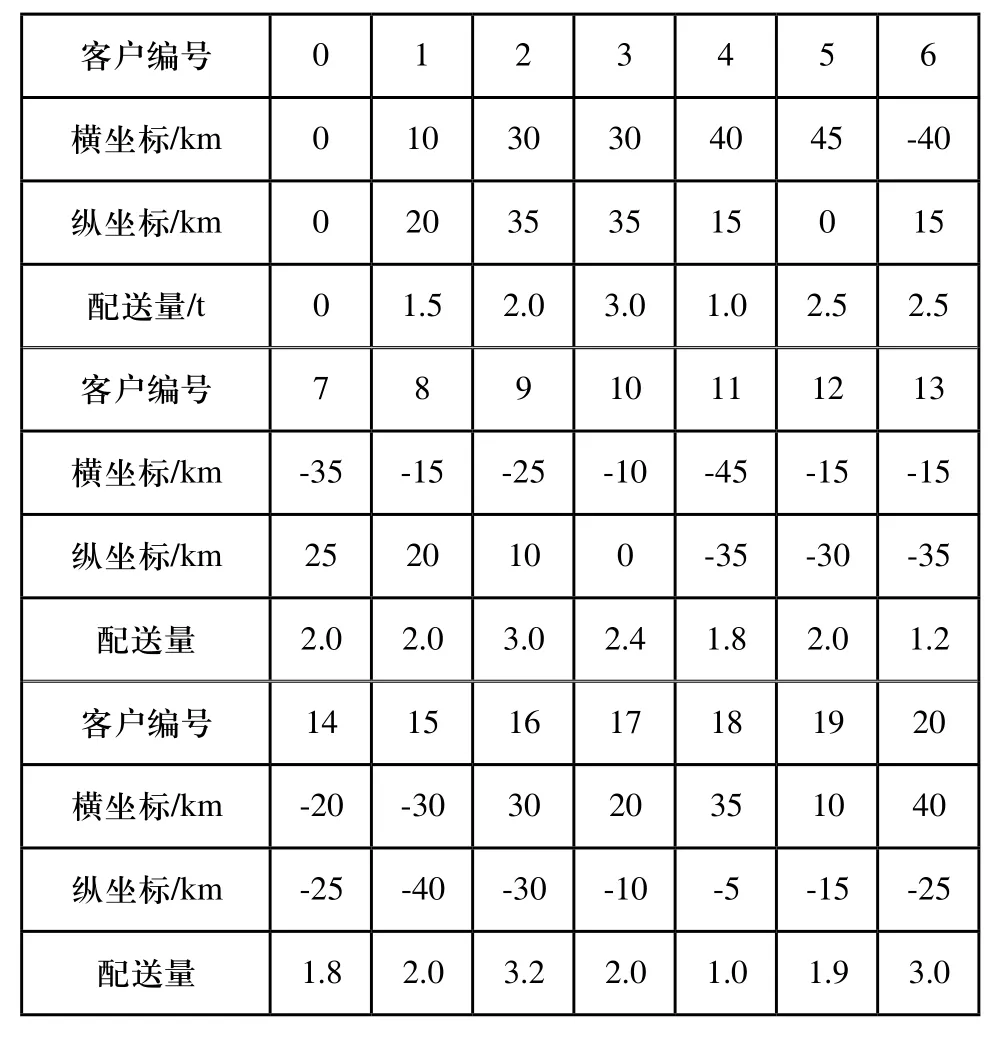
表1 客户及回收中心基础数据

本文根据设计算法，运用Java语言编程求解，在win8 64（intel(R)Core™i7-7500U CPU @2.70GHz处理器）系统下运行时间约0.1s，得到车辆的最短行驶距离为468.967km，车辆回收路径为0-12-13-15-11-14-10-0-1-2-3-4-5-18-0-19-16-20-17-0-8-7-6-9-0。最优回收方案如下表2所示。文献[8]利用基本蚁群算法，求解车辆回收路径最短距离479km，回收路径为：0-1-2-3-4-5-0-8-7-6-9-10-0-14-11-15-13-12-0-17-18-20-16-19-0。

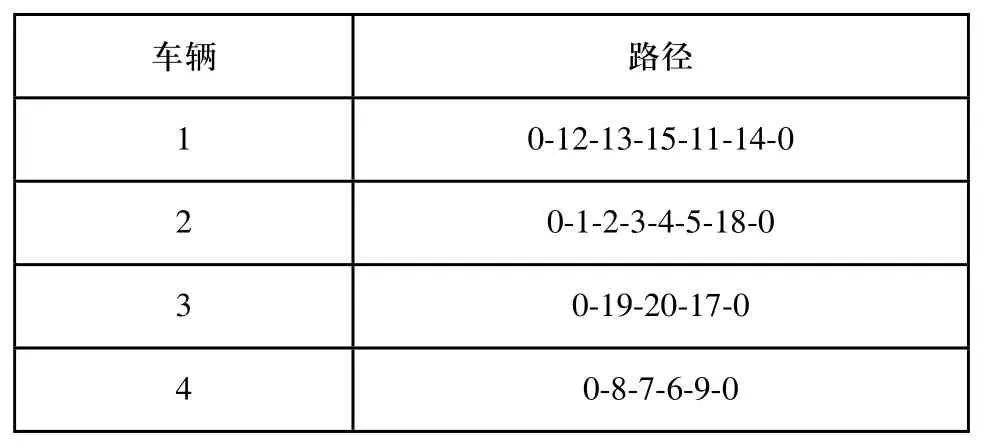
表2 最优回收方案

改进的蚁群算法求解结果相比基本蚁群求解结果，优化了10.003km。由图3可知，由最短距离趋势图可以看出，本文算法首次搜索到最优解的迭代次数为140次，收敛速度较快；从平均距离趋势图可以看出，均值大多低于479km，即优于文献[8]的最优解，且整体逐渐呈平稳趋势，解的质量越来越佳并趋于稳定。

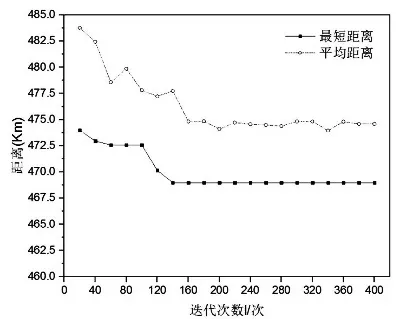
图3 算法收敛图

5 结论

逆向物流车辆路径优化是逆向物流领域研究的重难点。有效提高物流回收效率，减少车辆行驶距离以降低物流回收成本，彰显逆向物流的经济价值，对整个社会的绿色发展具有重大意义。本文针对基本蚁群算法进行动态改进，混合2-opt算法，实验结果表明改进的蚁群算法不仅寻优能力强，收敛速度快且结果比较稳定，对解决逆向物流车辆路径问题有一定参考价值。