反Heyting代数中MT理想及其性质

冯丹丹， 吴洪博

(陕西师范大学 数学与信息科学学院，陕西 西安 710062)

Heyting代数是作为直觉主义命题逻辑的代数模型引进的，使得逻辑排中律一般不再成立.事实上，Heyting代数是通过蕴涵运算对应的伴随关系而提出的一个数学结构.王国俊利用反蕴涵运算对应的伴随关系提出了一个数学结构，称为反Heyting代数，并指出反Heyting代数和Heyting代数不是自对偶的[1].目前，对Heyting代数的研究比较深入[2-9]，其中吴洪博等利用对偶范畴的思想方法和MP滤子的特征，在BR0代数和正则FI代数中提出了MT理想的概念[8-9].本文首先将MT理想的概念引入到反Heyting代数中，讨论了MT理想的等价条件和他的基本性质；然后给出了反Heyting代数的MT理想的几种生成方法；最后，在反Heyting代数中提出了素MT理想、极大MT理想以及次极大MT理想的概念，并且讨论了这些特殊理想的性质以及相互关系.

1 预备知识

定义1.1[1]设D是格，若对于D的任意元a与b，存在D的元a←b满足：∀c∈D有c≥a←b当且仅当c∨a≥b，则称D为反Heyting代数.

事实上，设D是反Heyting代数，因为D是格，故D非空，因此，∃a∈D,又因为∀c∈D,有c∨a≥a，所以c≥a←a，因此a←a为D中最小元，将a←a记作0.

命题1.1[1]设D是反Heyting代数，∀a,b,c∈D有：

1a←a=0;

2a∨a←b=a∨b;

3b∨a←b=b;

4a←b∨c=a←b∨a←c.

命题1.2[10]设D是反Heyting代数，∀a,b,c∈D有：

1a←b←c=a∨b←c;

2a←b←c=b←a←c;

3a←0=0;

4a≥b当且仅当a←b=0;

5a←b←b←c←a←c=0;

6a∧b←c=a←c∨b←c;

7a←b←c≥a←b←a←c.

命题1.3[1]若D是反Heyting代数，则D为分配格.

命题1.4[1]若D是只含有限个元的分配格，则D是反Heyting代数.

命题1.5[1]若D是反Heyting代数，则∀a,b∈D，a←b=minx∈D:x∨a≥b.

Zorn引理[11]设P是非空偏序集，若P的每个全序子集在P中有上界，则P必有极大元.

2 反Heyting代数中MT理想的概念

定义2.1设D是反Heyting代数，∀I⊆D,

1若I满足以下条件:

i0∈I;

ii∀a,b∈D，若a,a←b∈I,则b∈I,

则称I为D的MT理想.

2设I是D的MT理想，若∃a∈D,且a∉I,则称I为D的真MT理想.

本文用ID表示反Heyting代数D中全体MT理想构成的集族，即

I(D)={I⊆D:I是D的MT理想}

命题2.1设D是反Heyting代数，I是D的非空子集，则I是D的MT理想当且仅当I满足：∀a,b∈D，1I是下集；2当a,b∈I时，有a∨b∈I.

证明：(充分性)i因为I是非空，所以∃a∈D，因为0是D的最小元，因此0≤a，结合I是下集可知：0∈I;

ii当a,a←b∈I时，由2知a∨a←b∈I，又由命题1.12知a∨a←b=a∨b,因此b≤a∨a←b，由I是下集可知b∈I;

综上，I是D的MT理想.

(必要性)i若a∈I，∀b≤a，由命题1.24知a←b=0，故a←b∈I.又I是D的MT理想，结合定义2.1知b∈I,因此I是下集；

ii∀a,b∈I，由命题1.14知a←a∨b=a←a∨a←b=a←b.由命题1.13知b∨a←b=b，所以a←b≤b，因此a←a∨b≤b，由于I是下集，所以a←a∨b∈I,再由I是D的MT理想知a∨b∈I.

命题2.2 设D是反Heyting代数，∀a∈D,令↓a=b∈D:b≤a，则↓a是D的MT理想.

证明:1因为0≤a，所以0∈↓a;

2∀x,x←y∈↓a，即x≤a，x←y≤a，又因为x∨x←y=x∨y，故

y≤x∨y=x∨x←y≤a∨a=a

即y≤a，所以y∈↓a.

综上,↓a是D的MT理想.

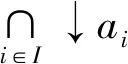
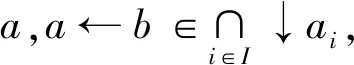
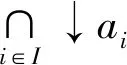
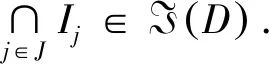
证明:∀Ij:j∈J⊆ID，

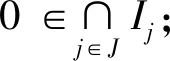
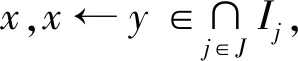
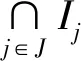
3 反Heyting代数中MT理想的生成方法

定义3.1设D是反Heyting代数，S是D的非空子集，如果D中包含S的最小的MT理想存在，则称这个最小的MT理想是由S生成的MT理想，记作S.

命题3.1设D是反Heyting代数，S是D的任意非空子集，则由S生成的MT理想必定存在，并且S=∩I:I∈I(D),S⊆I.

证明:1D⊆D且D是D的MT理想，所以I:I∈I(D),S⊆I≠φ;

2i由命题2.4知∩I:I∈I(D),S⊆I是D的MT理想；

iiS⊆∩I:I∈I(D),S⊆I;

iii∀J∈I(D)，S⊆J，有∩I:I∈I(D),S⊆I⊆J;

故∩I:I∈I(D),S⊆I是D中包含S的最小的MT理想，即

S=∩I:I∈I(D),S⊆I

命题3.2设D是反Heyting代数，S是D的非空子集，则S={x∈D:∃s1,s2,…,sn∈S,使得s1∨s2∨…∨sn≥x}.

证明:1令B=x∈D:∃s1,s2,…,sn∈S,使得s1∨s2∨…∨sn≥x，

i因为S非空，故∃s∈S，又0≤s，故0∈B;

ii∀x,y∈D，若x，x←y∈B，由B的定义知，存在a1,a2,…,an,b1,b2,…,bm∈S，使得

a1∨a2∨…∨an≥x，b1∨b2∨…∨bm≥x←y

所以a1∨a2∨…∨an∨b1∨b2∨…∨bm≥x∨x←y=x∨y≥y，因此根据B的定义知y∈B.

综上，B是D的MT理想.

2∀s∈S，有s≥s，故s∈B，因此S⊆B,因此B是D中包含S的MT理想.

3设I1是D的任意MT理想且S⊆I1，∀c∈B，由B的定义知∃c1,c2,…,cn∈S，使得c1∨c2∨…∨cn≥c,又S⊆I1,所以c1,c2,…,cn∈I1,又I1是D的MT理想，由命题2.1知c1∨c2∨…∨cn∈I1且I1是下集，故c∈I1，因此B⊆I1.

综上，B是包含S的最小MT理想，即S=B.

命题3.3设D是反Heyting代数，S是D的非空子集，则S={x∈D:∃s1,s2,…,sn∈S,使得s1←(s2←…(sn←x)…)=0}.

证明:利用命题1.21、4可直接证明.

4 反Heyting代数中的素MT理想

定义4.1设D是反Heyting代数，∀I⊆D，

1设I是D的MT理想，如果I满足：∀a,b∈D，a←b∈I或b←a∈I，则称I为D的素MT理想；

2设I是D的MT理想，如果对于D的任意MT理想J，当I⊆J时，有I=J或J=D，则称I为D的极大MT理想；

3设I是D的MT理想，a∈D，如果I在不包含a的MT理想中极大，即a∉I，且若M∈I(D)，I⊆M，则I=M或a∈M，则称I为关于a的次极大MT理想.

命题4.1设D是反Heyting代数，若I是D的素MT理想，则∀a,b∈D，当a∧b∈I时，有a∈I或b∈I.

证明:∀a,b∈D，当a∧b∈I时，由I是D的素MT理想知a←b∈I或b←a∈I，再由命题1.26知：

(a∧b)←a=(a←a)∨(b←a)=b←a，(a∧b)←b=(a←b)∨(b←b)=a←b

因此(a∧b)←a∈I或(a∧b)←b∈I，又因为I是D的MT理想，所以有a∈I或b∈I.

命题4.2设D是反Heyting代数，并且满足条件∀a,b∈D，有a←b∧b←a=0.则D的MT理想I是素MT理想当且仅当∀a,b∈D，当a∧b∈I时，有a∈I或b∈I.

证明:(必要性)命题4.1已证.

(充分性)∀a,b∈D，由于a←b∧b←a=0，又I是D的MT理想，所以a←b∧b←a∈I，故a←b∈I或b←a∈I，因此I是D的素MT理想.

命题4.3设D是反Heyting代数，若I是D的极大MT理想，则I是D的素MT理想.

证明:下面用反证法予以证明.

假设存在D的极大MT理想I不是D的素MT理想，由定义4.1(1)知：∃a,b∈D，有a←b∉I且b←a∉I，令GI,a=x∈D:∃c∈I,使得c←a←x=0.

1下证GI,a是D的MT理想.

i因为I是D的极大MT理想，故0∈I，且0←a←0=0←0=0，所以0∈GI,a；

ii∀x,x←y∈GI,a,∃c1,c2∈I，使得：

c1←a←x=0,c2←a←x←y=0

由命题1.2(1)知

c1∨a←x=c1←a←x=0

c2∨a∨x←y=c2∨a←x←y=c2←a←x←y=0

再由命题1.24知c1∨a≥x，c2∨a∨x≥y，所以

y≤c2∨a∨x≤c2∨a∨c1∨a=a∨c1∨c2

即a∨c1∨c2≥y，因此c1∨c2≥a←y，故c1∨c2←a←y=0，因为I是D的MT理想，由命题2.1知c1∨c2∈I，再根据GI,a的定义知，y∈GI,a，故GI,a是D的MT理想.

2下证b←a∈GI,a.

因a∨b←a=a,所以b←a≤a，由命题1.24知a←b←a=0，又0∈I，且0←(a←(b←a))=0←0=0，再由GI,a的定义知b←a∈GI,a;

3下证I⊆GI,a.

∀m∈I，有a∨m≥m，所以m≥a←m，故m←(a←m)=0，由GI,a的定义知m∈GI,a，因此I⊆GI,a;

4下证a←b∉GI,a.

假设a←b∈GI,a，则∃c3∈I，使得c3←(a←(a←b))=0，又因为

a←(a←b)=(a∨a)←b=a←b

因此c3←(a←b)=0，由命题1.2(4)知c3≥a←b，又因为I是D的MT理想，由命题2.1知I是下集，故a←b∈I，这与原假设a←b∉I矛盾，所以a←b∉GI,a.

结合1、2、3知GI,a是真包含I的MT理想，并且由4知GI,a≠D，这与I是极大MT理想矛盾，因此原假设不成立.

综上∀c,d∈D，有c←d∈I或d←c∈I，即I是D的素MT理想.

命题4.4设D是反Heyting代数，则∀a∈D-{0}，存在关于a的次极大MT理想.

证明:表示D中全体不含a的MT理想构成的集族.因为0是D的MT理想，故0∈，所以≠∅，按集合的包含关系构成偏序集.设{Ij:j∈J}是中的非空全序子集.

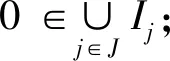
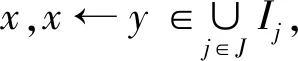
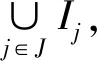
命题4.5设D是反Heyting代数，且满足条件：∀a1,b1∈D，有(a1←b1)∧(b1←a1)=0，则∀a∈D-{0}，存在不包含a的素MT理想.

证明:∀a∈D-{0}，由命题4.4知D中存在关于a的次极大MT理想I，下面用反证法证I是D的素MT理想.

假设I不是D的素MT理想，由定义4.11知：∃b,c∈D，使得b←c∉I且c←b∉I.令：

I1={m∈D:∃n∈I,使得n←((b←c)←m)=0}

I2={m∈D:∃n∈I,使得n←((c←b)←m)=0}

1下证I1，I2是D的MT理想.

i因为I是D的MT理想，故0∈I，又因为0←((b←c)←0)=0←0=0，所以0∈I1;

ii∀x,x←y∈I1，由I1的定义知∃y1,y2∈I，使得：

y1←((b←c)←x)=0,y2←((b←c)←(x←y))=0

由命题1.21知

(y1∨(b←c))←x=y1←((b←c)←x)=0

(y2∨(b←c))←(x←y)=y2←((b←c)←(x←y))=0

由命题1.24知y1∨(b←c)≥x，y2∨(b←c)≥x←y，所以有

y≤x∨y=x∨(x←y)≤(y1∨(b←c))∨(y2∨(b←c))=y1∨y2∨(b←c)

所以(y1∨y2)←((b←c)←y)=(y1∨y2∨(b←c))←y=0，又因为y1,y2∈I，且I是D的MT理想，故由命题2.1知y1∨y2∈I，所以由I1的定义知y∈I1.

综上知I1是D的MT理想，同样的方法可以证明I2是D的MT理想.

2下证c←b∉I1且b←c∉I2.

若c←b∈I1，则∃y1∈I，使得y1←((b←c)←(c←b))=0，又因为

(b←c)←(c←b)=(c∨(b←c))←b=c←b

所以y1←((b←c)←(c←b))=y1←(c←b)=0，因此y1≥c←b，又I是D的MT理想且y1∈I，由命题2.1知I是下集，所以c←b∈I，与原假设c←b∉I矛盾，因此c←b∉I1，同理b←c∉I2，所以I1≠D且I2≠D.

3下证c←b∈I2，b←c∈I1.

因为∀y∈I，y←((b←c)←(b←c))=y←0=0，由I1的定义知b←c∈I1，又由于∀y∈I，y←((c←b)←(c←b))=y←0=0，由I2的定义知c←b∈I2，所以b←c∈I1且b←c∉I,c←b∈I2且c←b∉I.

4下证I⊆I1且I⊆I2.

∀y∈I，因为y∨((b←c)←y)=y，故(b←c)←y≤y，因此y←((b←c)←y)=0，由I1的定义知y∈I1，即I⊆I1，同理I⊆I2.

5下证a∉I1或a∉I2.

若a∈I1且a∈I2，则存在y1,y2∈I，使得

y1←((b←c)←a)=0，y2←((c←b)←a)=0

由命题1.2(1)知

(y1∨(b←c))←a=y1←((b←c)←a)=0

(y2∨(c←b))←a=y2←((c←b)←a)=0

由命题1.24知y1∨(b←c)≥a，y2∨(c←b)≥a，再由命题1.3知D是分配格，所以有

a≤(y1∨(b←c))∧(y2∨(c←b))≤((y1∨y2)∨(b←c))∧((y1∨y2)∨(c←b))=

(y1∨y2)∨((b←c)∧(c←b))=(y1∨y2)∨0=y1∨y2

又y1,y2∈I且I是D的MT理想，由命题2.1知y1∨y2∈I且I是下集，所以a∈I，这与a∉I矛盾，所以a∉I1或a∉I2.

结合1、2、3、4和5知I1和I2是真包含I的MT理想，且a∉I1或a∉I2，这与I是关于a的次极大MT理想矛盾，所以原假设错误，因此I是D的素MT理想.

命题4.6设D是反Heyting代数，并且满足条件：∀a,b∈D，有a←b∧b←a=0，∀I∈ID，则下列条件等价：

1I是D的素MT理想；

2若I=A∩B，其中A,B∈ID,则I=A或I=B;

3∀I1,I2∈ID，若I1∩I2⊆I,则I1⊆I或I2⊆I.

证明:1⟹2 若I=A∩B，其中A,B∈ID,假设I≠A且I≠B，又由于I⊆A且I⊆B，故∃a∈A且a∉I,∃b∈B且b∉I.下证a←b∉I且b←a∉I.

若a←b∈I，则a,a←b∈A，又A是D的MT理想，由MT理想的定义知b∈A，又b∈B,故b∈A∩B=I,这与b∉I矛盾，所以a←b∉I;

若b←a∈I，则b,b←a∈B，又B是D的MT理想，由MT理想的定义知a∈B，又a∈A,故a∈A∩B=I,这与a∉I矛盾，所以b←a∉I;

综上，a←b∉I且b←a∉I，这与I是D的素MT理想矛盾，所以原假设错误，因此I=A或I=B.

2⟹3∀I1,I2∈ID，若I1∩I2⊆I,令I3=I1∩I2,则I3⊆I，又由2知I3=I1或I3=I2，所以I1⊆I或I2⊆I.

3⟹1∀a,b∈D,∀x∈↓a←b∩↓b←a，则x∈↓a←b且x∈↓b←a，即x≤a←b且x≤b←a，所以x≤a←b∧b←a=0，因此x=0，所以↓a←b∩↓b←a=0，由I∈ID知0∈I，因此↓a←b∩↓b←a⊆I,又由3知↓a←b⊆I或↓b←a⊆I，所以a←b∈I或b←a∈I，故I是D的素MT理想.