液压振动台位移补偿的PID控制方式的研究∗
何少佳 闫奥博 祝新军 纪效礼
(①桂林电子科技大学机电工程学院,广西桂林541004;②绍兴职业技术学院,浙江绍兴312000)
随着我国对高端装备的不断投入。如何去提高装备的可靠性的问题,已经越来越引起制造业企业的高度重视,这也是我国高端制造的必经之路[1]。
当前,模拟产品在运行、存储等过程中所受到的振动激励一般通过振动模拟设备来模拟[2]。我国目前的振动模拟设备通常采用液压振动台,但我国液压振动台始终处于中低端水平。其主要原因是位移控制精度不高,则振动激励的模拟效果大打折扣。
通过仿真建立一个高精度的数学模型很难模拟液压振动台系统。主要原因是其存在工艺复杂、系统参数时变、冲击振动等复杂因素[3-4]。虽然传统的PID控制器对其输出效果有所改善,但是固定的PID参数值并不能解决系统自适应能力低,响应滞后等性能缺陷。
对液压振动台位移的控制一般转换为对电压值的闭环控制[5],通过中央处理器处理将电压值转换为相应的位移值。在运行过程中,由于液压泵中压力的损失,造成的位移变化不能直接反映出来,加上传统的PID控制器的调节,液压振动台系统的位移的控制精度和稳定特性等性能严重受到影响。
因此,本研究在前人提出的理论研究的基础上,提出在液压振动台的液压泵中加入压力传感器检测液压泵的输出压力值,与设定的位移值形成双闭环控制,单神经元网络的PID控制系统对反馈回来的位移和压力值进行处理,对位移误差进行在线补偿。
1 研究现状
目前,为了了解液压振动台系统的位移精度控制方面的问题,我国的一些学者对其做了一些研究,比如胡红波[6]提出了一种位移反馈控制系统,以减小振动台输出波形的失真度,但是系统的自适应能力低;晁智强[7]提出了一种基于PID控制和重复控制补偿符合控制策略,但由于定值PID的局限,自适应低,加上液压泵内部的压力的损失等因素的影响,导致系统稳态精度不高;黄茹楠[8]采用常规PID控制和模糊控制策略对振动台实施控制,有效地抑制了超调量和提高了动态特性;严侠[9]提出了一种单神经元PID位移控制系统,有效地提高了系统的自学、和自适应能力。
虽然液压振动台的位移控制精度问题在一定程度上得到了改善,但是与实际的液压振动台系统存在较大的差异。当受到外界干扰时,很难获得高精度的位移控制效果。因此,进一步改善液压振动台的位移控制精度的研究有着重要的意义。
2 液压振动台位移误差补偿的方案
由于液压振动台硬件系统结构复杂,直接精准地控制液压振动台的伺服作动器的位移非常困难[10]。我国大部分液压振动台对位移的控制一般转换为对电压值的闭环控制,通过处理器处理将电压值转换为位移值,但是这样存在较大的误差。在运行过程中,由于液压泵中压力的损失,造成的位移变化不能直接地反映出来,严重影响了液压振动台位移的控制精度。
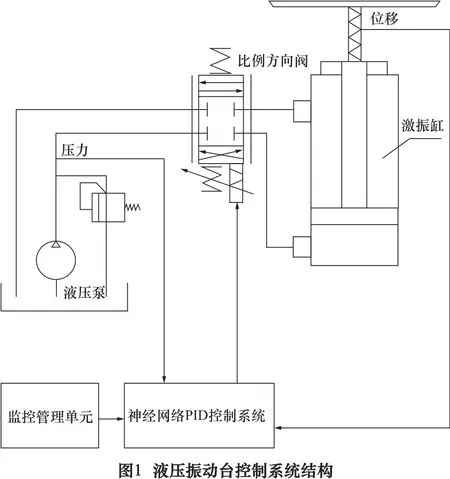
为了改善液压振动台的位移控制精度,研究在液压泵的输出口处加入压力传感器的方法,来检测液压泵的输出压力,从而实现对液压振动台位移误差的补偿。液压振动台控制系统结构图如图1所示。
在监控管理单元里预先设置好液压振动台的位移值和液压泵的压力值。神经网络PID控制系统给比例方向阀电量信号,比例方向阀的流量和方向在其控制下发生变化,按照程序执行,改变伺服作动器的位移。通过位移传感器获得伺服作动器的位移值,实现对位移的控制,液压泵的压力值通过压力传感器获得,并将其转换为电量参数反馈到控制系统中,从而实现对压力值的控制,来减小液压振动台在运行中由于振动、油液泄漏等因素带来的液压泵内部的压力损失,导致位移的变化。监控管理单元,对设定的参数值和实际反馈回来的数值进行比较和处理,通过神经网络算法,不断修正输出的参数,使输出的效果不断趋于最优化。这种控制方式可以减小外界干扰对系统的影响。
3 单神经元网络的PID控制
在工业领域中,应用常规的PID控制,对精准的数学模型的调节有着极其重要的作用[11]。但对于液压振动台这种复杂的数学模型,应用常规的PID控制则不能满足其伺服作动器的控制需求,表现出自适应能力低、反应迟钝等弊端。基于单神经元网络的PID智能控制,不但结构简单,而且具有自学习和自适应能力,有较强的抗干扰能力和鲁棒性[12]。
3.1 单神经元运算过程的原理
为此,本研究针对液压振动台的伺服作动器,引入单神经元网络的PID智能控制,不仅能适应环境的变化且有较强的鲁棒性。按照有监督的Hebb学习法则,单神经元网络的PID智能控制器对加权系数不断地调整从而实现自适应和自组织功能,进而改善其伺服作动器的位移控制精度和抗干扰能力以及鲁棒性[13]。有监督的Hebb学习法则可表示为:

式中:Δwij(k)为神经元i、j的联接权值;η为学习速率;dj(k)为期望输出;oi(k)、oj(k)为神经元i、j的激活值。其运算过程结构图如图2所示。
图2中:x1,x2,…,xn为神经元网络神经元接收到的外部环境信号,wi1,wi2,…,win为神经元的联接权。
3.2 液压振动台系统单神经元PID控制器的设计
采用基于单神经元网络的PID和有监督的Hebb学习法则的智能控制器,对液压振动台系统反馈的位移值和压力值与设定值进行比较和处理,产生的误差通过具有自学习和自适应功能的单神经元网络的PID控制器,从而调整出最优的PID的控制参数,实现对液压振动台的伺服作动器进行闭环控制。液压振动台系统的单神经元网络PID控制器的拓扑图如图3。
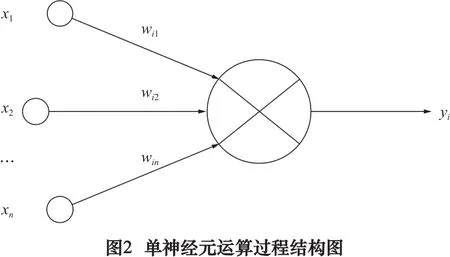

图3中:lin1是液压振动台伺服作动器的位移,pin2是液压泵的压力;y1、y2是系统反馈的位移值和压力值;xp(k)、xi(k)、xd(k)是神经网络中神经元所接收到的外部信号。控制算法及学习算法为[14]:
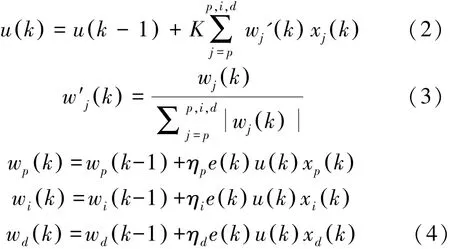
式中:xp(k)=e(k),xi(k)=e(k)-e(k-1),xd(k)=Δ2e(k)=e(k)-2e(k-1)+e(k-2);ηp、ηi、ηd分别表示比例、积分和微分的学习速率;K为神经元的比例系数,K>0。
程序开始运行,首先给u(0)赋初值,然后单神经元网络的PID按照有监督的Hebb的学习法则调整出最优的权值参数,来适应外部环境的改变,从而迅速地减小系统的稳态误差,使系统达到最优化。
4 仿真验证
本研究针对液压振动台位移误差的补偿调节,是加入压力值与位移值形成双闭环控制来对位移值进行补偿。伺服作动器的位移值y1与液压泵中输出的压力值y2互相影响,构成双输入双输出的耦合非线性的系统。假设系统被控的位移和压力的近似数学模型[13]为:
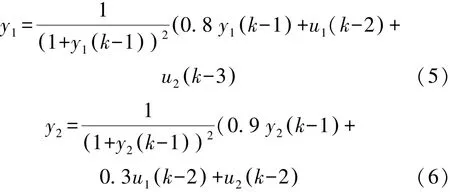
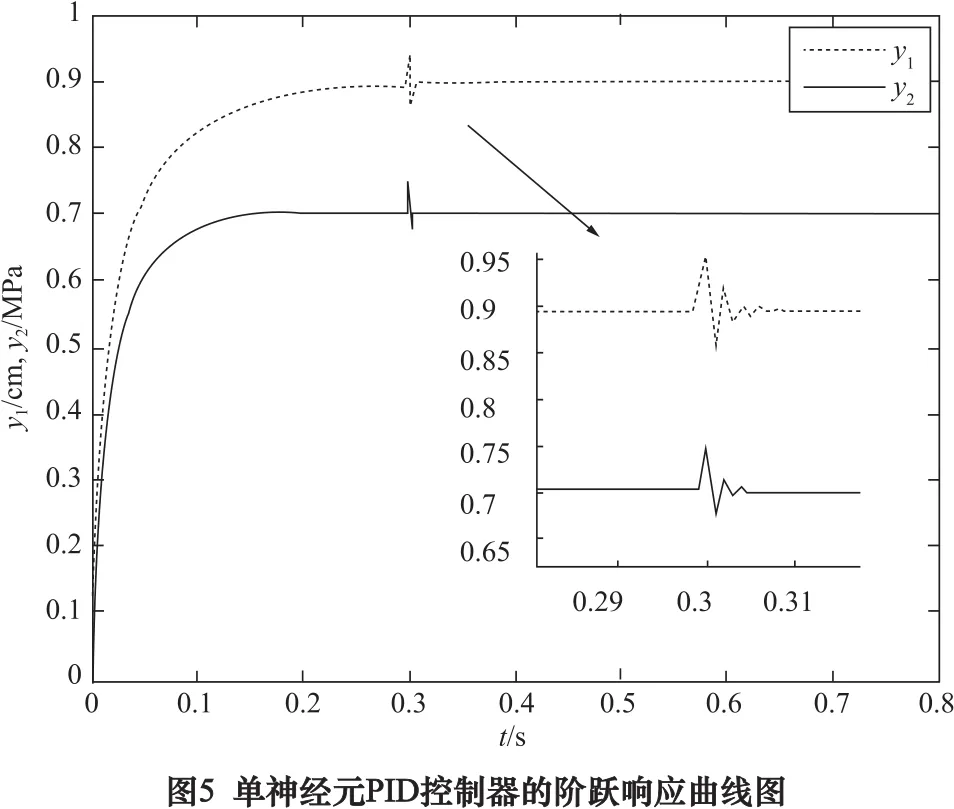
式中:y1、y2分别对应为位移传感器和压力传感器反馈的相应参数;u1、u2分别对应为位移和压力的单神经网络控制器的输出;假设设定的阶跃信号参数分别为:rin1=0.9 cm、rin2=0.7 MPa。 当系统处于稳态时,在第0.3 s采样时刻,分别加入0.05 cm、0.05 MPa的外界干扰。传统PID控制器的阶跃响应曲线图如图4所示,单神经元PID控制器的阶跃响应曲线图如图5所示。
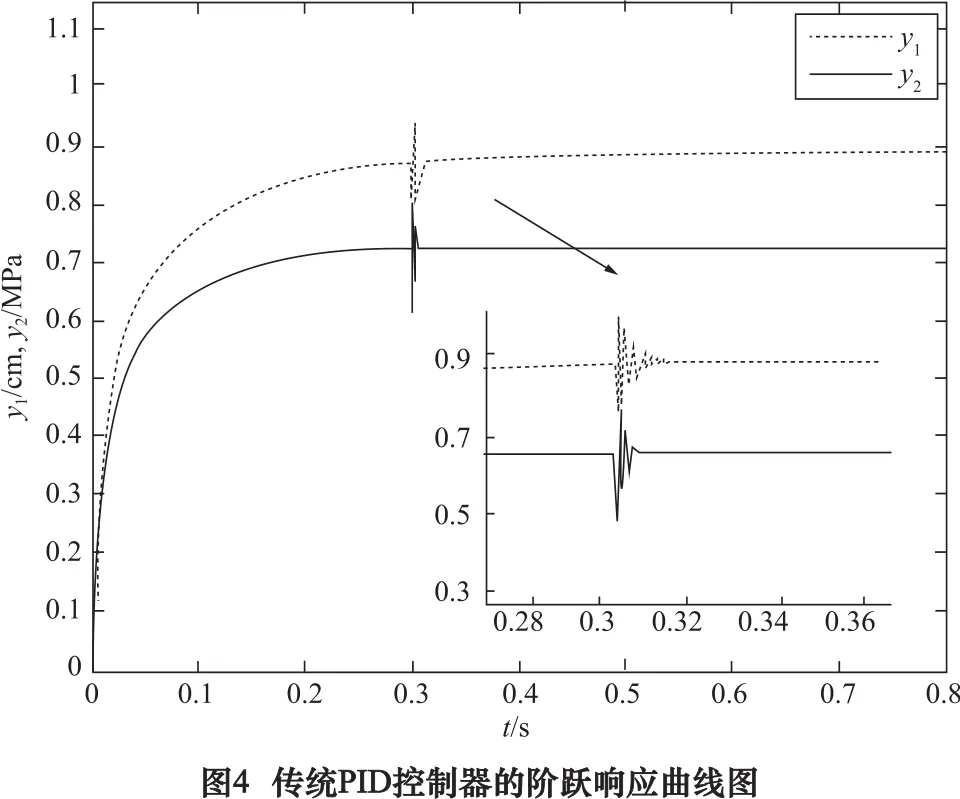
由图4和图5的对比可知,采用基于单神经元网络的PID和有监督的Hebb学习法则的智能控制器,响应速度更快,能迅速达到所设定的参数值[15]。当受到外界干扰时,能迅速反应,并快速地回到稳定状态,因此相比于常规的PID控制方式,其具有更精准和快速的位置控制的特点,可以有效地解决液压振动台在运行过程中位移控制的问题。
5 结语
本研究通过在液压泵中加入压力传感器,其压力值与位移值形成双闭环控制来对位移值进行补偿,以减小液压振动台在运行过程中所受到的干扰等问题造成的位移误差。通过采用基于单神经元网络的PID和有监督的Hebb学习法则的智能控制器来调整出最优的PID的控制参数,从而改善其伺服作动器的位移控制精度和抗干扰能力以及鲁棒性。

