航空发动机中回热器传热和阻力性能的数值模拟

林 坤

（西安航空职业技术学院，陕西西安710089）

间冷回热航空发动机能够在很大程度上提高航空发动机的性能与节能环保水平。椭圆形管回热器是一种十分先进的回热器结构，其具备十分突出的优势，即传热特性。而既有数值研究基本上都是以多孔介质模型作为载体，根本无法切实反映回热器的内部流场，不仅如此，通过整体式模型，还需具备大型服务性，并耗费大量计算时间。因此，进一步详细分析椭圆回热器传热与阻力性能，实现回热器结构优化具有非常重要的现实意义[1]。

1 航空发动机中回热器传热与阻力性能

1.1 传热与阻力性能

构建椭圆形管回热器模型，具体几何参数值如表1所示。通过进行网络无关联分析，能够获得最终数值所计算的独立解，并合理设置边界条件和数值方法，以此计算分析，以此获取传热与压降数值计算结果[2]。结果显示，椭圆形管回热器的努赛尔数与压降都会在雷诺数的影响下出现变化，呈正向关系，并且在雷诺数不断增大的趋势下，压降增加的幅值会明显上升[3]。

表1 椭圆形管回热器模型几何参数值 mm

对椭圆形管回热器传热与阻力性能进行详细分析，热性能指标太过单一，无法明确回热器性能的优劣，因此应全面考虑传热与压降等相关要素。对此，利用总熵增率法，以能量为基础对回热器传热与阻力性能进行评估。其中，在既定单位时间内回热器所产生的损失主要包括压力与温度两部分。所谓总熵增率实际上就是给回热器传输单位热量的时候，消耗的可用能源，也就是随着总熵增率不断变小，那么回热器综合性能就会随之提高。而椭圆形管总熵增率会在雷诺数不断增大的趋势下逐渐提高，所以说，椭圆管回热器综合性能是在雷诺数增大的影响下逐渐减小的，雷诺数越小，综合性能就会越好。总熵增率计算公式为

式中：Q为回热器在单位时间内的平均换热量，J；T1与T2为流体进出口温度，℃；qv为流体体积流量，m3/s；Δp为压降，Pa；T0为环境温度，℃；Ys为总熵增率。

1.2 结构参数影响

合理选择重复段作为数值计算对象，以此有效降低模拟计算量，并保证回热器结构具备一定程度的对称性和重复性。选择4种不同结构尺寸，改变椭圆形管的长轴与短轴，促使回热器的椭圆形管截面面积相同，模型长宽相同，设置无量纲参数为椭圆管的长短轴比[4]。具体不同模型几何参数如表2所示。

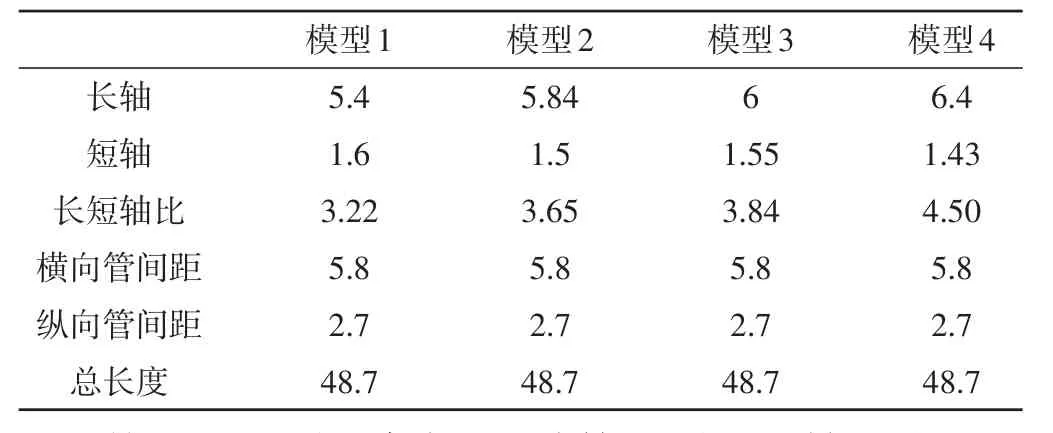
表2 不同模型几何参数 mm

管间距相同的条件下，计算不同长短轴回热器的传热与压降数值，可以得知，在无量纲参数在长短轴比逐渐增大的影响趋势下，努赛尔数不会发生太大改变，但是压力梯度会逐渐缩小。而在长短轴比相同时，努赛尔数和压力梯度会直接受雷诺数增大的影响，随之逐渐增大。这主要是因为雷诺数增加，导致流体流速增大，从而快速冲洗了传热壁面，边界层变薄，流体换热得以强化。而且流体流速增加会使得椭圆形管对流体造成的阻力增大，而产生的压力损失也会增大。但是，长短轴比对压降影响明显大于传热，所以，在传热满足的基础上，可以适度提高长短轴比，以缩减压力损失，减少损耗。通过4种不同椭圆形管长短轴比回热器的总熵增率计算，可以发现，总熵增率会在雷诺数增加的趋势下，不断增大，也就是说回热器综合性能会随之减小。而在雷诺数相同的基础上，随着长短轴比增大，总熵增率会逐渐减小，即回热器的综合性能会在长短轴比增加的影响下，不断提高。

1.3 布管方式影响

在椭圆形管结构参数既定的基础上，横向间距与纵向间距都会直接影响回热器的传热与压降性能。其一，横向间距的影响。椭圆形管尺寸相同时，横向间距的扩大，会导致努赛尔数随之缩小，压降则是呈现先减小然后再增大的状态。横向间距对传热的影响明显较大，因此，在满足压降的基础上，应该适当缩减横向间距，以此降低压力损耗。为了综合对比分析传热与阻力性能，引用总熵增率法，其中总熵增率会在雷诺数的影响下随之变化，即回热器综合性能会在雷诺数增加的趋势下不断下降，而在雷诺数相同时，横向间距越大，总熵增率的变化趋势为先行减小再有所增大，即在横向间距增加的趋势下，回热器的综合性能会呈现出先升高再下降的状态。但是还需注意的是，横向间距越大，那么其对于回热器综合性能造成的影响也会逐渐减小。其次，纵向间距影响。在管间距相同时，纵向间距不断增大，努赛尔数和压降会不断缩小。为了对比分析传热与阻力性能，引用总熵增率法，其中总熵增率会在雷诺数明显增加的影响下逐渐提高，也就是说回热器综合性能会随着雷诺数增加不断减小。而在雷诺数相同时，纵向间距不断扩大，总熵增率则会逐渐减小，也就是在纵向管间距逐渐扩大的情况下，回热器的综合性能会大大提高。但是，纵向间距越大，对综合性能的影响会不断减小[5-6]。

2 航空发动机中回热器的结构与性能优化

2.1 截面形状优化

基于传热学理论，回热器传热过程公式为

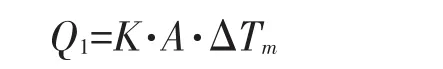
式中：Q1为热负荷；K为总传热系数；A为换热面积，m2；ΔTm为冷热流体对数平均温差，℃。

在回热器生产与设计优化时，可以采取总传热系数提升、换热面积扩大、对数平均温差提高等措施，促使传热性能得到有效提升。但是，如果工艺基础相对稳定，那么物料温度一般不会随意变化，总传热系数也不会出现太大改变，所以，在椭圆形管中添加平行段，以此扩大换热面积，提高传热性能，实现截面形状优化。

选择4种不同结构尺寸，改变平椭圆形管的平行段长度与高度，促使回热器截面面积相同，长宽相同，并与椭圆形管回热器的模型3进行比较分析。设置无量纲参数为平行段长度与高度比，具体几何尺寸参数如表3所示[7]。

2.1.1 传热与阻力性能

在管间距和长宽度相同时，对不同尺寸的平椭圆形管回热器进行数值模拟计算，并与椭圆形管回热器进行比较，可以发现，平椭圆形管努赛尔数明显较大，也就是说平椭圆形管回热器的传热性能明显更具优势。在雷诺数逐渐增大的趋势下，努赛尔数与压降也逐渐增大。其中，模型4的传热性能最优化，而模型3的阻力性能最优化。

表3 不同模型几何参数 mm

2.1.2 综合性能

为了综合比较分析传热与阻力性能，引入总熵增率法，并与椭圆形管回热器进行比较分析，可以发现，总熵增率法会在雷诺数增加的趋势下，逐渐增大，也就是说回热器综合性能与雷诺数之间呈反向关系。而在雷诺数既定时，平椭圆形管总熵增率明显较小，也就是说平椭圆形管回热器的综合性能明显更具优势。其中，模型3的综合性能最优化。

2.2 结构参数影响

随着平椭圆形管的平行段长高度比不断增大，努赛尔数与压降呈先减小后增大的趋势，但是整体上并未出现太大波动。而通过合理利用总熵增率法进行对比，可以发现，在雷诺数既定的基础上，平行段长高度比越大，总熵增率法则呈现先减小后增大的状态，而在长高度比为0.713时，回热器综合性能最优化。

2.3 布管方式影响

其一，横向间距影响。在间距逐渐扩大的影响下，努赛尔数与压降不断缩小，而且压降降低速度逐渐减小，横向间距对于传热的影响相对较大。而利用总熵增率法进行对比，可知如果雷诺数是既定的，那么横向间距越大，总熵增率就会呈现先减小后增加的趋势，也就是在横向间距增加的影响下，回热器综合性能则会先提高再降低。其二，纵向间距影响。在间距不断扩大的趋势下，努赛尔数与压降会随之缩小。通过引用总熵增率法比较分析，可知，既定雷诺数条件下，纵向间距越大，总熵增率则会随之减小，综合性能就会不断增强，而且在间距不断增大的形势下，总熵增率的下降速度与综合性能提高速度都会有所减缓[8]。

3 基于场协同原理强化回热器传热与阻力性能

基于场协同原理针对回热器进行强化传热研究，回热器的场协同原理就是利用调整冷热流体的流动方式，提高回热器性能。流体的换热强度与流速、温度梯度以及两者夹角相关（协同角θ）。

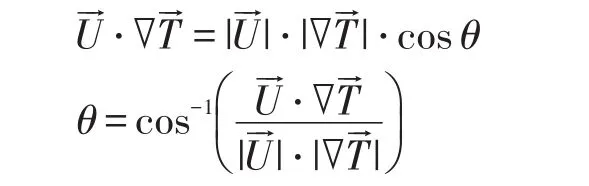
从公式中可知，温度梯度和速度方向保持一致或相反的状态下，回热器处于最佳状态，效果最优，因此，可以适当以减小协同角的方式实现传热强化。基于全局协同角，体积平均协同角是最为常见的，其公式为

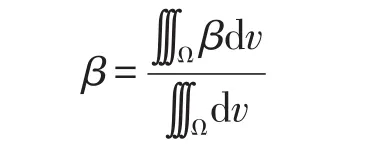
通过计算可知，椭圆形管回热器与平椭圆形管回热器的场协同角变化趋势始终一致。在回热器的进口位置处，在一定范围下，速度和温度夹角的变化会越来越小。但是，在回热器内部，协同角会发生很大幅度的波动，且存在一定的周期性。平椭圆形管回热器的场协同角波动比较大，这就说明平椭圆形管回热器的结构具备强有力的强化传热效果[9-10]。

4 结论

通过上文分析可知，航空发动机回热器的努赛尔数与压降会在雷诺数增加的趋势下不断增大，而总熵增率会随着雷诺数增加则增大，所以回热器综合性能在雷诺数越小的状态下最佳。为了进一步保证强化传热性能，实现了椭圆形管截面形状优化与改善，并详细分析了平椭圆形管回热器，通过比较分析传热与阻力性能，可知，在管间距、截面面积与长宽度相同的基础上，平椭圆形管的努赛尔数明显要大，所以说平椭圆形管回热器的传热性能更好。而平椭圆形管回热器与椭圆形管回热器的场协同角变化趋势始终保持一致，而平椭圆形管回热器的场协同角波动比较强烈，这就代表着平椭圆形管结构具有明显的强化传热效果。