基于小波变换与中值滤波的炉膛火焰图像去噪方法研究
梁利利
(咸阳师范学院,陕西咸阳712000)
近年来,随着工业的快速发展,锅炉燃烧的稳定性与安全性开始备受社会各界积极关注,而实时有效检测炉膛火焰是保证锅炉运行安全的重要途径。因此,在炉膛火焰燃烧状态检测中,积极利用先进的机器视觉技术,以此有效解决图像噪声污染问题,确保图像预处理与后续处理工作顺利进行。图像噪声的类型很多,其中高斯噪声与脉冲噪声的影响最为突出。图像去噪算法就不同处理区域可以划分为频域法与空域法[1]。通过深入分析图像特点、噪声特性与频谱规律等,提出了大量相应的图像去噪算法。因为噪声主要集中在高频区域,图像频谱大多分布于低频区域,就此规律,采取低通滤波法。其中有很多处理算法都可以用在图像滤波中,在空域中开展平滑滤波是一种有效的图像去噪方式,即均值滤波法,主要通过邻域像素点灰度值的平均值代替中心像素点灰度值。尽管空域平滑滤波算法的计算流程相对简单,但是极易造成图像细节模糊。因此,在图像处理领域,寻找可以保持图像细节信息的算法一直都备受关注,而中值滤波可以有效处理这一问题,在滤除脉冲噪声的基础上,确保图像边缘信息不受影响,但是却无法恰当处理高斯噪声,同样会导致细节损伤。然而,以小波变换为基础的阈值去噪算法能够很好地控制高斯与均匀分布,其中小波变化具有其自身的独特特性,即分辨率多、选基灵活、去相关性,在频域与时域中,表征信号局部信息的能力非常突出,能够瞬态分析,所以在图像去噪中备受青睐[2]。
1 小波变换与中值滤波图像去噪
1.1 小波变换图像去噪
小波变换能够科学有效消除高斯噪声,而且在小波域中合理设置阈值,能够更进一步消除噪声分量,然后基于小波变化恢复原始信号。因为小波变换可以集中原始信号能量到相对较大的系数中,并把噪声能量分散到许多系数中,所以,噪声小波的系数相对要小一些。科学合理设置与之相适应的阈值函数,以消除比较小的小波系数,并保证较大的小波系数不会发生变化,这时便能够快速有效消除噪声。一般阈值函数主要包括两种,即硬阈值函数与软阈值函数。其中,硬阈值函数具有整体性,而缺乏连续性,使得图像去噪后悔出现一定的吉布斯问题。但是,软阈值函数不仅整体性较好,而且连续性也比较突出,但是,因为小波系数比较大的时候,所处理的系数与原系数间一直存在着一定程度偏差,从而对重构信号与真实信号差异的缩小有着直接性影响,以此导致重构信号存在较大误差。为了避免这两者的不足,构造新阈值函数已为必然趋势[3]。去噪图像的一般模型为

式中:X为噪声图像;f为理想图像;σ为方差;e为噪声。去噪目标为从含噪声的图像中获取长度为n的理想图像的逼近图像,促使在误差预估状态下,逼近图像为理想图像的最近最优状态。把图像行列分别做小波变换,就能够获得原图像各个频率状态的子图,对其进行三级小波多尺度分解,具体结果如图1所示。LL为低频分量,HL为竖直方向边缘细节,LH为水平方向边缘细节,HH为45°与135°方向的细节,由此可知,小波变换具备非常明显的细化与局部分析能力优势。

图1 正交小波分解图
1.2 中值滤波图像去噪
中值滤波器以次序统计为载体恢复信号,这是一种最具代表性的非线性滤波器,其本质在于将数字图像某点的值用其邻域中各个点值的中值加以替换。首先,就所选窗口,确定中心位置在原始图像中的重合方式。其次,在图象上移动扫描窗口;再次,将窗口对应值合理排序,并将中间值赋予窗口中心位置。一般情况下,中值滤波所选择的窗口样式各式各样,即线形、方形、圆形等等,不同样式窗口的去噪效果也明显各不一致[4]。
1.3 改进自适应中值滤波算法
自适应中值滤波是以中值滤波为基础,就窗口的灰度值中值为依据,对滤波模板进行适当调整。其中,窗口最大灰度值用Gmax表示,最小灰度值用Gmin表示,中值灰度值用Gmid表示。在Gmin<Gmid<Gmax的时候,窗口的尺寸如果没有变化,那么就适当扩大尺寸,直到找到最为恰当的滤波窗口,或达到窗口最大值。随后,对中心点像素灰度值进行检测,其用G(x,y)表示,在Gmin<G(x,y)<Gmax的时候,输出灰度值,或者用Gmid替代灰度值。
中值滤波效果会在滤波模板尺度不断增大的趋势下得到明显改善,但是自适应中值滤波效果却不甚显著。不过中值滤波与自适应中值滤波之间存在着一定程度上的滤波盲目性与非自适应性,难以预先判断图像噪声。据此,采用改进自适应中值滤波算法。在自适应中值滤波中最后的关键环节,因为Gmid提取的是滤波窗口灰度值中值,势必会受图像噪声影响,所以,必须采取行之有效的方法措施全面消除噪声造成的不利影响[5]。
就m×m滤波窗口,探测像素极值为Gmin与Gmax,平均值为Gave。
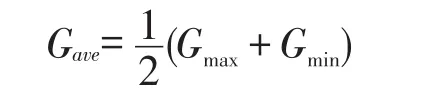
检测异常点,并对窗口各个像素点与平均值进行对比分析。

像素点划分为异常点与正常点两种,其中,异常点主要包含噪声点与边缘点,而没有被污染的就是正常点,以像素点间距为依据对异常点进行检测。在图像中,边缘点相互连接的,具有一定的连续性,但是噪声点却是独立存在的,这样便能够大体上辨别出噪声点。

在噪声分离之后,其余像素点便是正常点,进行排序并获取中间值,以此作为滤波结果输出。
2 基于小波变换与自适应中值滤波相结合的炉膛火焰图像去噪方法
想要有效消除炉膛火焰图像噪声,尤其是高斯噪声与椒盐噪声,应切实有机结合小波变换与自适应中值滤波。先对原始图像进行自适应中值滤波,再进行小波分解,以生成系数矩阵,对子带的小波系数而言,可以利用中值滤波加以处理,并生成全新的系数矩阵,使用此矩阵重新构建图像。基于小波变换与自适应中值滤波相结合的炉膛火焰图像去噪算法流程具体如图2所示。

图2 算法流程

图3 不同方向中值滤波
在经过小波分解之后,图像各个频带都会带有一定的方向性,其中,HL子带为基于行经过低通滤波,基于列经过高通滤波,然后获得子图像,其具备垂直边缘方向性。LH子带为图像基于垂直方向经过低通滤波器的高频信息与水平方向经过高通滤波器的低频信息,其具备水平边缘方向性。HH子带为基于水平方向的低通滤波与垂直方向的高通滤波之后,获取子图像,其具备对角线边缘方向性。把炉膛火焰图像进行三级小波分解之后,LL子带选用低通滤波,LH子带选用水平方向中值滤波,HL子带选用垂直方向中值滤波,HH高频子带选用对角线中值滤波。然后,通过子带小波系数重新构建小波,以此获得去噪图像。具体如图3所示[6-7]。
3 实验结果讨论与分析
采用 Intel CPU Pentium 43.2 GHz,2 GB 内存,Matlab2012作为实验平台。为了证明基于小波变换与自适应中值滤波相结合的炉膛火焰图像去噪方法的科学性与有效性,选择数字图像处理实验的代表性标准图片Lena灰度图像进行实验,图像大小为512×512,从中添加0.02强度的高斯噪声与0.05强度的脉冲噪声相混合的噪声,采用VisuShinrk算法、高斯混合模型算法以及小波变换与中值滤波相结合算法对含混合噪声的图像进行去噪处理[8]。具体实验结果如表1所示。
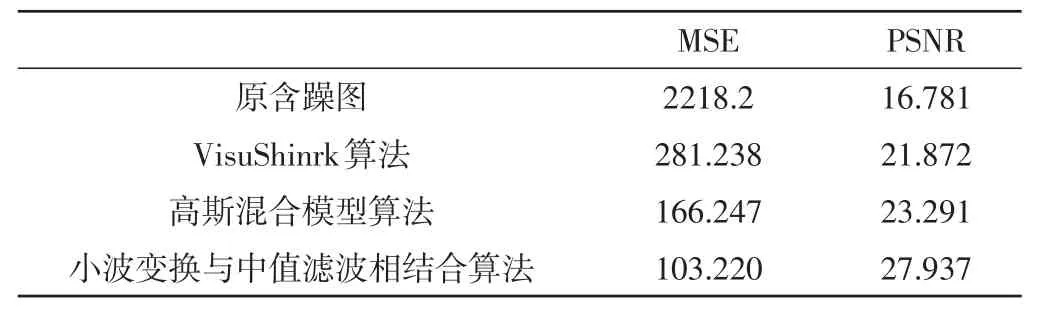
表1 三种方式对Lena图去除混合噪声实验结果
从中可知,这三种方法中,小波变换与中值滤波相结合的算法均方误差(MSE)是最小的,峰值信噪比(PSNR)是最大的,所以,此算法在去除混合噪声中的效果最佳,具有非常突出的去噪能力,而且从表中还可以看出,高斯混合模型算法的去除混合噪声效果明显优于VisuShinrk算法。并且,采取这三种方法,小波变换与中值滤波相结合的算法的图像视觉效果最佳,而且能够相对彻底清除干净高斯噪声与脉冲噪声,其中的纹理细节处理的也非常清晰,细节部分明显可辨,边缘部分保存也比较完整,去噪效果十分显著[9-10]。
4 结论
总之,在图像实际应用中,会同时收高斯噪声与椒盐噪声的污染,这样的图像中,不仅包括椒盐噪声,还包含高斯噪声,对于这种含躁图像的去噪处理,如果单独利用中值滤波或者小波交换,根本无法根除噪声,效果都不甚理想。本文通过实践证明和实验分析,得出结论,可以切实结合小波交换与中值滤波算法,以此形成混合滤波算法,进行噪声去除,可以先使用中值滤波去除椒盐噪声,再使用小波阈值滤波去除高斯噪声,保持图像的边缘信息与细节部分,以实现去除所有炉膛火焰图像噪声的目标。

