基于核心素养背景下高中数学实验案例研究
江苏省射阳中学 徐长中
提高学生的数学核心素养是近几年数学教学所提倡的,尤其是高中数学教学,新课程标准指出,数学核心素养是指具有数学的基本特征、适应于个人终身发展和社会发展需要的数学思维品质和数学关键能力。因此如今的高中数学不仅仅是一门演绎科学,同时它也是一门人文科学,高中数学教学应更加注重数学素养的培养与积淀。数学实验是近几年高中数学教学中大力提倡的一种全新教学活动,经过案例的实践及反思,笔者认为数学实验教学对提升学生的核心素养有积极的作用。下文结合实例案例简要谈谈笔者对此的看法。
一、传统实验,发展数学分析能力
传统实验是指用教具、模型所演示的数学实验,是数学教学中最常见的实验教学方法,其实验的场所通常是教室,实验工具是数学教具或者生活常见物品。通过实物的演示,可以让平时“高冷”的数学更加接地气,便于学生对数学的理解,提高学生数学分析能力。
如《椭圆的标准方程》中,对椭圆第一定义的探索是教学的重点,直接告知学生定义显然不利于学生的理解,设计一个简单的数学实验即可将该抽象的内容变得生动形象,有利于学生对该定义的掌握。
实验场所:教室。
实验工具:白纸、图钉2 枚、绳子一根(25 厘米左右)、笔。
实验过程:在纸上任意选取两个点,记为F1,F2,将两枚图钉固定在F1,F2点处,将绳子的两端分别系在两枚图钉上,用笔尖把绳子拉紧,使笔尖在纸上慢慢移动,并观察当绳子的位置变化时所形成的图形。(完成过程:学生以小组为单位合作完成,后展示实验结果,教师深入学生指导)
通过小组合作,学生基本能顺利完成实验。
师:大家画出的图形是什么?
生(齐声回答):椭圆。
师:没错,是椭圆。大家画的时候应该观察到了,虽然绳子的位置会发生变化,但绳子的总长度却始终没变,因此大家能否用较为连贯的文字语言描述一下刚才所画图形的轨迹呢?
生1:椭圆是到两个定点的距离之和等于定长的点的轨迹。
师:同学们觉得他的描述是否准确呢?有没有需要补充的?
生2:应该在定义上加上“平面内”。
师:刚才同学们在画的时候老师观察到有一个小组刚开始没画起来,因为绳子没拉动,后来松了一下绳子,就画成功了,这是为什么?
生3:绳子的长度必须大于两定点之间的距离,即椭圆是平面内到两个定点的距离之和等于定长(大于两定点之间的距离)的点的轨迹。
师:你分析得真到位!
师(追问):那我们对比各组的椭圆,会发现有些椭圆比较“圆”,而有些则比较“扁”,这是为什么呢?
生4:在F1,F2长度不变的情况下,当绳子的总长度越长,画出的椭圆越“圆”,绳子越短则椭圆越“扁”。
师:没错,这是我们下一节课要讨论的内容,我们将会用数学语言“离心率”来刻画椭圆“圆”的程度。
师生共同总结:(椭圆的第一定义)平面内到两个定点F1,F2的距离的和等于常数(大于F1,F2)的点的轨迹叫作椭圆,两个定点F1,F2叫作椭圆的焦点,两焦点之间的距离叫作椭圆的焦距。
以上实验虽然简单,但是通过学生自己的动手操作、观察,对椭圆定义的理解、椭圆概念的描述及椭圆性质的预热都有促进作用。同时激发学生对解析几何的兴趣,让原本抽象的解析几何更形象。从师生交流中可以看到,学生在实验后能够根据实验过程及结果进行分析,他们的数学分析能力正在发展中。
二、计算机实验,提高数学思维活性
计算机实验,顾名思义,就是用计算机进行操作的实验,可以在教室进行,以教师演示为主,也可以在机房进行,让学生自己操作。这需要倚靠一些数学软件,以几何画板最为典型,同时,简单的数据处理也是必备的技能。通过计算机的实验,不仅能让学生熟悉对数学软件的操作,而且还能发展学生思维的活性。
实验场所:计算机房。
实验工具:计算机几何画板软件。
实验实施片段:
学生成果:
学生成果:

学生成果:

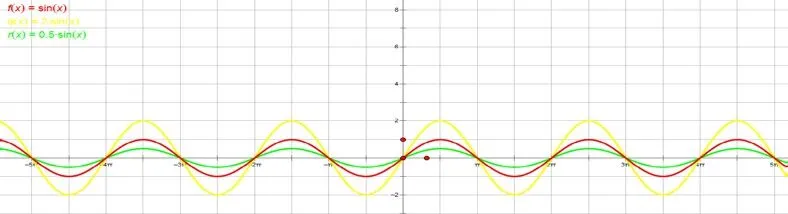
学生的操作任务相对简单,数据比较单一,便于他们操作。教师也可在此基础上进行动态演示,利用变化的数据更形象地描绘图像的变化规律。如右图:
一次计算机数学实验、一次上机操作让学生体会到数学原来是会“动”的,同时感受到科学的魅力,在实验探究的过程中可以有效提高思维的活性。

三、实验室实验,形成数学研究意识
数学实验室的建立是近几年中学数学发展的新追求,数学实验室拥有较完备的数学实验教学设备,如多媒体计算机及学生操作台、配套器材(各学段的学具及几何模型)、数字化设备( 图形计算器、数据采集器、传感器)、数学软件资源(动态数学网络软件、中小学教学资源、配套教材、图书资料) 等。在实验室进行实验教学,可以营造浓厚的实验研究氛围,给学生创造良好的实验研究环境,逐步培养学生的数学研究意识,提高学生数学研究能力。
如在《古典概型》的教学中让学生在数学实验室进行计算机模拟“蒲丰投针”实验,体悟概率产生的过程,了解概率的实质。
实验场所:数学实验室。
实验工具:计算机几何画板软件、Excel 软件。
实验实施片段:
由于该实验的设计过程较为复杂,教师在实施前可以通过网络下载该实验的模板,以便学生能在教学规定时间顺利实施该实验。在这个过程中学生只需根据提前下载好的资源包安装并运行模板,即可进行该实验。学生在实验中的任务有两个,一是运行该实验,二是将实验数据导出到Excel 表格中,通过数据推算其概率。
上文提到的该实验的模板也可以作为数学拓展课或者数学兴趣小组的教学资源,由教师引领学生开放设计实验流程,编写代码,拓宽学生的能力。但就这节课来说,重点是让学生通过实验过程推导实验结果,因此使用模板,让实验的演示过程简单化,提高学生的可操作性。除上述实验以外,本校还在实验室进行了“线性规划”“圆锥曲线方程”“对数函数的图像及性质”等多次实验,实验过程中学生总是充满兴趣与热情,通过这些实验,明显感觉到学生的探究能力得到了增强,数学研究意识也加深了,实验室内被学生对数学热爱的氛围所充斥着。
四、户外实验,挖掘数学应用价值
数学实验并非要在实验室或者教室进行,它还可以延伸到室外,甚至走出校园。户外实验更倾向于生活实验,让学生挖掘数学的生活价值,体会数学与生活的联系。
如在《等差数列的前n 项和》的教学中提到有关“复利”的问题,笔者在双休日即给学生布置了任务:(1)通过一定的方法理清单利和复利的区别。(2)走出家门,寻找有关“复利”的实际问题进行调查实验,撰写简单的实验报告。
在回收的实验报告中,学生基本上通过书本或者网络理解了复利的含义,知道了单利和复利的关系。有关实际问题的调查实验,大部分学生走访了公积金问讯处、售楼处、房产中介等场所,并且采集了样本进行分析。分析结果达到了预期的要求。
数学核心素养是新时代的高中生所必需的素养,基于核心素养背景下的高中数学实验教学是笔者与团队的一次尝试,尝试中有收获也有不足,本文是笔者对此的愚见,权当是抛砖引玉,希望同仁们能给出更好的意见和建议。在今后的教学中,笔者会不断反思与改进,争取在高中数学实验教学中更好地凸显数学核心素养的价值。

