生活中的数学问题与教学中数学意识的培养
甘肃省酒泉市第二中学 杨 瑛
在抽象的意义下,一切科学都是数学。在数学教学过程中,如何培养学生良好的数学意识与利用数学知识解决实际问题是终极目标;在学生学习数学的过程中,学生具备数学意识,构建数学模型,建立数学思维方法,以数学的视角看问题、解决问题,从而以最优的方法解决问题并创新是最高境界。
初中数学的教学目标指出:在培养学生的数学意识方面要求“逐渐掌握以数学的观点看问题、解决问题,综合应用数学理论解决实际问题,提高创新意识,增强理论联系实际的能力。”同时,在我们的日常生活中,像储蓄、债券、保险、购物、决策更是生活中不可避免的现实问题,都需要数学知识来解决。而由于数学应用意识,属于意识范畴,处于隐形状态,在应试教育的当下,极易被忽视。而在教材的编排上,却处处体现了数学应用意识的培养要求和有意识的应用数学知识去解决实际问题的内容。
一、解决数学问题,建立数学意识
【实例一】北京师范大学版数学,初二下学期二单元,一元方程组,第五节“不等式与一次函数”一节例题:东方传媒公司计划在国庆期间组织员工去胡杨林旅游,参与旅游的人数共有20 人。目前接触的A,B 两个旅行服务社的服务内容基本相同,服务价格均为200 元/人。经过协商,A 旅行服务社可以提供的七五折的折扣价格,B 旅行服务社给予八折的折扣,并且可以省去其中一人的所有费用,问这个单位选择哪家这次旅行的花费最少,成本最低?这样的数学应用问题,文字叙述较长,没有明确给出求什么,用什么知识解决,学生感到比较难。尽管学生已经学习了一次函数与一元一次不等式,但想不到用二者联合起来去解决问题,缺乏应用数学知识的意识。换种问法,把此问题细化成明确的数学问答,如:(1)设支付的费用为y,参与活动的人数是x,分别写出A,B 两个旅行社所支付的成本y 与总人数x之间的数学函数关系式;(2)参加旅游的人数在什么范围内选A 旅行社费用低于B 旅行社?(3)参加旅游的人数在什么范围内选B 旅行社费用低于A 旅行社?(4)会不会出现两家费用相同的情况?问题细化后,学生会从总费用随着人数的变化而变化,想到函数的思想,从而想到一次函数的增减性,写出两家旅行社与人数的函数关系式,结合一元一次不等式求解。解答过程:
设该单位参与活动的总人数为x,选择A 社进行服务时,所需的成本是y1元,选择B 社时,所需的成本是y2元,则:
y1=200×0.75x,即y1=150x,
y2=200×0.8(x-1),即y2=160x-160,
由y1=y2,得150x=160x-160,解得x=16,
由y1>y2,得150x>160x-160,解得x<16,
由y1<y2得150x<160x-160,解得x>16。
通过这样的实例,不仅使学生明白了解决此类问题的数学方法,而且学生把生活中遇到的实际问题与相应的数学模型连接起来,建立了数学意识与思维,提高了同学们的学习能力。
二、解决实际问题,发展数学意识
【实例二】北师大版九年级数学上册第四章《图形的相似》第六节,利用三角形相似测高。根据旗杆的高度,综合运用三角形相似的判定定理和相似三角形的定义解决问题,发展应用意识。
1.通过影子计算旗杆的高度,如图1

图1
计算过程:教师让一个学生在旗杆前站立,阳光照射到学生与旗杆时地上形成影子,测量两段影子BE 与BD 的长度,如图2。

图2
∵光线是平行入射的,∴AE ∥CB,∴∠AEB =∠CBD,
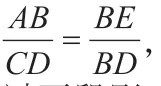
经过推算得出:通过两段影子的长度BE 与DB 以及人的高度AB,我们利用方程得出CD 的长度,即旗杆的高度。
2.利用标杆测量旗杆的高度
计算过程:教师让一名同学参与解题,教师在学生与旗杆间插入一根标准杆,杆的长度预先已经测量完毕,教师要求学生不断移动位置,保证学生的眼睛、旗杆与标杆的顶端三者在同一直线上,这时老师测量学生脚分别与标杆、旗杆之间的位移,根据标准杆的长度以及两个位移量,计算出旗杆的长度。如图3。

图3
如图3,过点A 作AN ⊥DC 于N,交EF 于M。
提示:∵学生、标准杆与旗杆都是与水平面垂直的,∴∠ABF=∠EFD =∠CDH =90°,
∴学生、标准杆、旗杆是相互平行的。
∵EF ∥CN,∴∠1 =∠2,∵∠3 =∠3,
∵学生与标准杆的位移、学生与旗杆的位移,标准杆与学生高度差异EM 都是已知量,
∴能求出CN,∵∠ABF =∠CDF =∠AND =90°,∴四边形ABND 所组成的图形为矩形。
∴DN =AB,∴能求出旗杆CD 的高度。
3.利用镜面反射求解旗杆的高度
操作方法:仍然是让一名同学参与,这次学生与旗杆之间垂直放一面镜子,要求学生移动自己的位置,直到学生在镜子里面可以看见旗杆的顶端。这时老师测量出学生与镜子的位移以及旗杆与镜子之间的位移,以此计算出旗杆的高度。
图4
∵反射角=入射角,∴∠CED =∠AEB,∵学生、旗杆直立于地面,90 度垂直,∴∠B =∠D =90°,∴
经过测量学生、旗杆与反射镜子之间的位移,已知学生的身高,就可以利用方程求出旗杆的高度CD。
初中数学教材中编排的实际问题实践活动探索课,往往由于受条件的限制与应试教育的影响,而被老师忽视或者略过。其实,实践活动课是以问题为载体,学生自己动手参与探索求知的过程,是数学知识活化的过程,也是积累数学活动经验,达到培养学生遇到实际问题要有数学意识的关键。
三、遇到问题,思维意识数学化
培养学生有意识地利用数学概念、理念和意识去解决日常实践过程中的问题。同学们在平时的生活中经常碰到一些需要用数学知识来描述的现象。当遇到这样的一些现象时,学生若有一定的应用数学的意识,善于从数学的角度,利用数学思维去表达与理解这些现象,就会开启数学奥秘的大门。
例如,在各类比赛活动中,评委人数一般是奇数,并且最后得分总是去掉一个最高分与一个最低分,然后求其他数据的平均数,这样做的原因是什么?学生学习了数据的分析与整理,了解了平均数,中位数等知识后,就能有意识地去运用这些知识去分析这一现象,并能给出合理的解释,实际上就是体现了应用数学的意识。再解决“在两个汽车站之间,怎样设加油站的位置,使得到两个汽车站的距离最小”这样的问题时,同学们就会在脑海中浮现,关于最短路问题的数学理论。在学生的思维模式中渗透数学意识,使学生建立起应用数学知识解决问题的数学意识,学数学,用数学的目的自然就达到了。
数学思维是通过数学的视角,以数学的观点来探索生活中与数字、空间几何有关的现象,发现问题以及人们的心理活动与思想意识上的反映。在数学课的教学中,要抓住教材这一载体,渗透建立激发学生的数学意识。

