金珠水库拱坝坝肩抗滑稳定分析论证

石从浩，杨 柳，马富强

（贵州省水利水电勘测设计研究院，贵州 贵阳 550002）

1 概况

金珠水库位于纳雍县西北部约72 km的昆寨乡凹猪河村上，距离昆寨乡政府约3km。水库枢坝址以上流域面积为26.7km2，多年平均流量0.546 m3/s，水库总库容1100万m3,兴利库容834万m3。推荐坝型为碾压混凝土拱坝方案。坝顶高程为1599 m，水库正常蓄水位为1595 m，最大坝高68.5 m。工程等别为Ⅲ等，工程规模属中型。

其中大坝为碾压混凝土双曲拱坝，坝顶高程1599 m，河床建基面高程1530.5 m，最大坝高68.5 m；顶坝弧线长度为198.76 m，坝顶弦线长度为179 m，顶拱中心角75°；坝顶宽5.5 m，拱冠梁处最大拱厚18 m，大坝厚高比0.263。大坝主体C9020W6F50三级配碾压混凝土；大坝上游迎水面采用50 cm厚C9020W6F50二级配变态混凝土；变态砼层之后采用C9020W6F50二级配碾压混凝土防渗层。

2 计算方法

拱坝坝肩抗滑稳定分析有多种方法，常用的方法有刚体极限平衡法、有限元计算法和地质力学模型实验法。其中在拱坝坝肩抗滑稳定分析方法中，刚体极限平衡法为基本方法，刚体极限平衡方法有二维的刚体极限平衡法和三维的刚体极限平衡法。

二维的刚体极限平衡法进行坝肩抗滑稳定分析，一般采用单位高度的水平拱来计算各个高程的坝肩基岩稳定，并确定各个高程必需的坝肩基岩等高线范围。在计算中不考虑坝体和岩体铅直重量的抗滑作用，如果各个高程的水平拱的坝肩稳定都能满足设计要求，就可以保证整个坝肩基岩稳定。

三维刚体极限平衡法进行坝肩抗滑稳定分析，视滑动体为刚体，不考虑各部分的相对位移进行拱端的整体稳定分析。

2.1 二维刚体极限平衡法

采用《拱坝坝肩岩体稳定分析》(王毓泰，周维桓等编著)[1]中计算方法，取单位高度（z=1 m）的拱圈作为计算单元对坝肩抗滑岩体进行平面稳定分析。计算时选择一个底滑面和侧滑面组成的滑动模式。

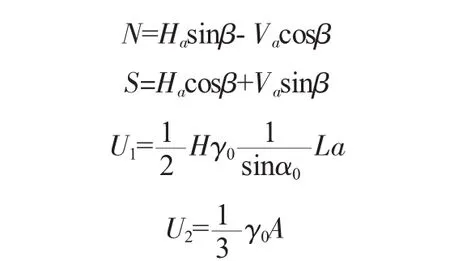
图1 二维刚体极限平衡法计算简图计算公式如下：

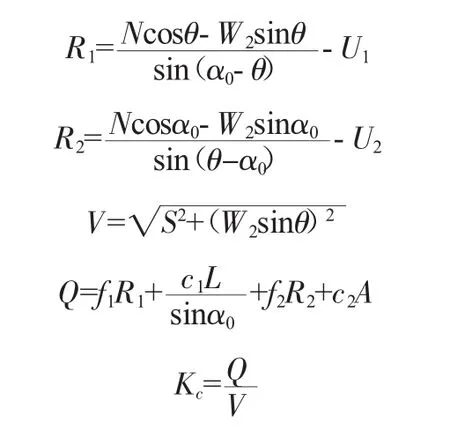
计算简图见图1。式中：N及S为由拱端传来的轴向推力Ha和剪力Va在侧向滑移面AC上的法向力及滑移力；β为滑移面与Ha的夹角；W2为抗滑岩体ABC的重量；U1、U2为陡、缓结构面上的渗透压力；H为滑移面的平均水头（上下游水位差）；γ0为水容重；L为滑移面的长度；α0为高倾角结构面的倾角；θ为缓倾角结构面的倾角；α 为渗透压力系数，一般 α=0.4～0.5，取 α=0.4；c1为陡倾角结构面的粘着力；c2、A为缓倾角结构面的粘着力及面积；f1、f2为陡、缓结构面上的摩擦系数。

2.2 三维刚体极限平衡法

图中的ABGF为拱坝建基面，AEJF为拱端上游拉裂面(简称P1)，作用荷载为水压力，EDIJ为侧滑面(简称P2)，FGHIJ为底滑面(简称P3)，块体上的作用有：Ha为拱端轴向力，位于水平面内；Va为径向剪力，位于水平面内；V’c(=Vctanθ)为梁底剪力，位于水平面内；U1为垂直作用于P1面的渗透压力；U2为垂直作用于P3面的渗透压力；U3为垂直作用于凡面的渗透压力；W为坝体及坝基滑块的总重量，垂直向下，W=W1tanθ+W2，W1tanθ为作用在块体上的坝体和水体自重W2为块体自重[2]。

图2 三维刚体极限平衡法计算简图首先计算侧滑面和底滑面上的反力R2和R3，以及沿侧滑

计算简图见图2。面P2和底滑面P3交线方向J的分力S；坝肩滑块抗滑稳定安全系数K1利用下式求解：

式中：f2、c2、A2为侧滑面P1上的摩擦系数、黏聚力、滑动面积；f3、c3、A3底滑面 P3上的摩擦系数、黏聚力、滑动面积。

3 地质条件和地质参数

址区为单斜构造，无大断裂构造发育，岩层产状305°～315°∠70°～85°，右岸岩层倾角变化较大，左岸变化较小，多在80°以上，坝区岩性为砂质泥岩、含泥质细粒粉砂岩，黄色泥岩，节理裂隙较发育。

3.1 结构面参数

表1 岩体物理力学参数建议值

3.2 地质裂隙统计

坝址区裂隙发育统计情况见表2。3.3 分析对象及岩体物理力学参数

以拱坝的左坝肩为抗滑稳定分析对象，底滑面采用岩层层面的抗剪断参数，侧滑面抗剪断参数是由岩石/岩石和裂隙面按连通率加权平均计算所得，见表3。

表2 坝址区裂隙发育统计表

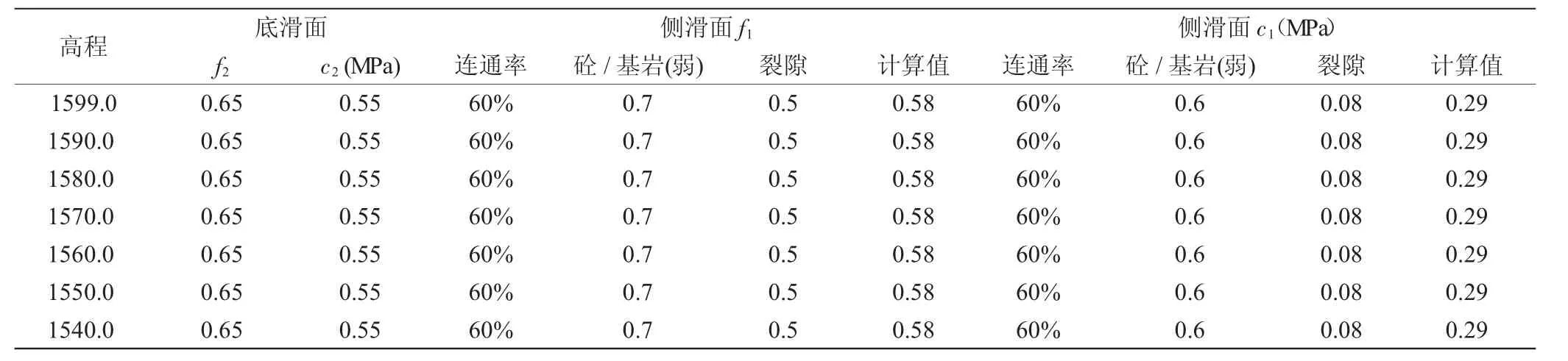
表3 左坝肩抗滑岩体物理力学参数换算表

4 坝肩稳定计算分析

4.1 滑动面的选取

二维和三维刚体极限平衡法滑动面选取的原则一致，左岸侧滑面和底滑面选取如下：

左岸侧裂面4组裂隙中裂隙③50°～60°/∠80°～85°与各层拱圈拱端径向均成较小夹角，对坝肩抗滑稳定最不利，以裂隙③作为右坝肩的抗滑稳定计算的侧裂面。

左岸底滑面坝址岩层产状为310°∠80°，岩层倾角80°较陡不能作为底滑面；分析实际存在的裂隙组合，发现左岸的裂隙组合均倾角较陡，不能作为底滑面；因此，假定一组层面作为底画面，该底滑面倾角按0°处理，底滑面的地质参数取弱风化岩体参数。

4.2 二维刚体极限平衡法计算成果（表4）

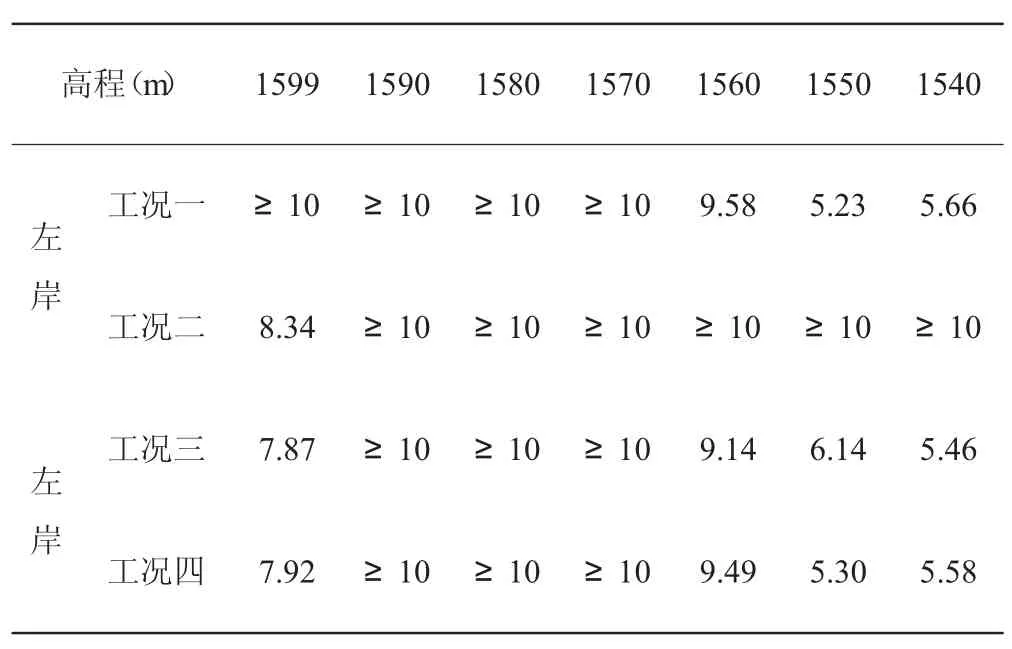
表4 二维刚体极限平衡法稳定计算成果表

4.3 三维的刚体极限平衡法计算成果（表5）

表5 三维刚体极限平衡法稳定计算成果表

4.4 两种计算方法对比评价

从上述计算结果可知，按照二维刚体极限平衡法，其稳定系数大于二维的刚体极限平衡法计算成果。计算结果是偏于不安全。当采用二维分层稳定计算方法每个高程的层面都考虑了底滑面的抗剪因素，而三维分层稳定计算方法只考虑一个底滑面的抗剪因素，三维刚体极限平衡法更加接近拱坝坝肩的破坏模式，因此在实际工程运用中，应该采用多种方法进行拱坝的坝肩稳定分析，更好地评价拱坝的坝肩稳定。

5 结语

通过上述两种计算方法，对金珠水库大坝坝肩抗滑稳定做了一个较为全面的分析论证，计算结果表明，在各个工况下，坝肩抗滑稳定安全系数均满足《混凝土拱坝设计规范》SL 282-2018[3]的要求。