基于逐步回归法的BP神经网络在大坝渗流分析中的应用

谢文群

（江西省大余县水库工程管理局，江西 大余 341500）

大坝安全监测资料分析方法常用统计模型、确定性模型和混合模型[1]等，这些模型均建立在数理统计的基础上，影响因子的选择是模型精度关键之一，根据不同影响因素的确定方法，统计模型又可划分为逐步回归法、差值回归法，正交多项式回归法等，不同方法所建立的计算矩阵带宽不同，计算速率及精度也有较大差异。

人工神经网络模型是基于模仿生物大脑的结构和功能，采用数学和物理方法构成的一种信息处理系统或计算，由于具有非线性映射、分类和聚类、优化计算等特点，被广泛用来解决不同种类数据之间的复杂关系，根据网络结构的不同，神经网络又可划分为误差反向传播神经网络（BP模型）、Hopfield神经网络、Boltzmann机等[2]，仲云飞等[3]提出了利用遗传算法优化BP神经网络进行大坝扬压力预测，张国翊等[4]提出了变更传递函数倾斜以和动态调节不同学习速率的BP改进算法，提高了缺陷识别率。缪新颖[5]等人则基于LM-BP神经网络进行了大坝变形预测分析，在精度和训练速上得到了提高。

1 逐步回归模型

逐步回归分析方法基本思想是根据自变量对因变量的影响显著程度，将个因子逐步引入回归方程中，依据重要性，有选择性的剔除次要因子，直到显著因子全包括在回归方程以内为止，建立相对较为稀疏的计算矩阵，减小带宽，提高计算速率；另一方面，更直观了解影响因素，逐步分析法在进行异常原因分析，分析变化规律和发展趋势等方面发挥重大作用。如傅蜀燕等[1]确定了大坝变形主要原因，其表明计算量少、精度高等；陈兰等[2]利用逐步回归法较好的分析了边坡变形的变化规律和发展趋势。本文采用逐步回归法，结合某水库大坝测压管水位实测数据进行分析，为了解该水库渗流运行状态提供理论依据。

进行大坝渗流监测数据分析，首先需确定所有可能的影响因子，根据文献[1]可知，大坝渗流影响因素可能包括水位分量f（H），降雨分量R及时效分量。由于滞后效应，水位分量H包括当日库水位、前期库水位、坝基水位、下游水位等，降雨分量包括当时降雨量及前期降雨量，时效分量主要为筑坝土体结构的固结对渗流影响。

2 BP神经网络

2.1 标准BP神经网络

误差反向传播(Error Back Propagation，BP)学习算法具有无反馈的神经网络结构，采用有指导学习方式进行训练和学习，通过比较输出层各个神经元的实际输出与期望输出，获得二者之间的误差，按误差函数按梯度方向，调整各个连续权值，达到减少误差效果。

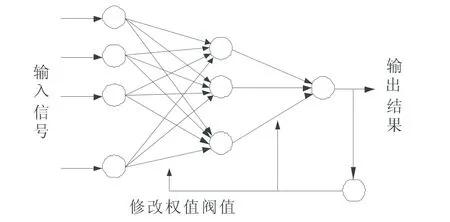
图1 典型三层BP神经网络结构图

正向传播：传递函数采用S型，按式(1)，将前一层作为输

入，得出的输出结果作为下一层输入，直至求得最终输出结果。

根据给定的期望输出，求出与实际输出的偏差为δtk：

其偏差期望为：

为使随着连接权值调整按梯度下降，按照误差按梯度下降原则，则有：

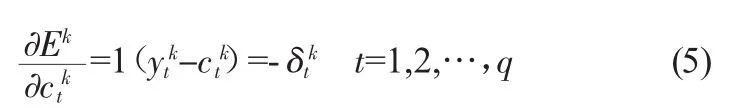
因此，隐含层至输出层的连接权值V调整值为：

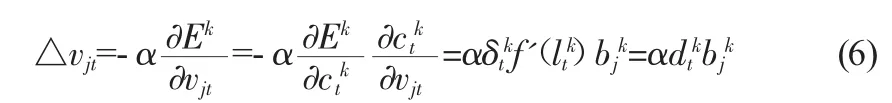
同理，连接权值w调整值为：

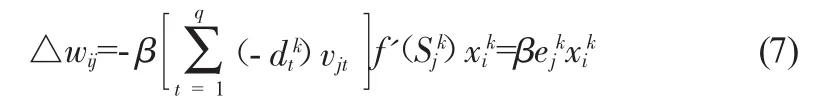
2.2 逐步回归-BP神经网络优化算法模型

由于标准BP网络的算法在最速下降法存在缺点，如学习算法的收剑速度慢、存在局部极小点、隐含层层数及节点数选取缺乏理论指导，训练时学习新样本有遗忘旧样本的趋势[6]。为此，可从两方面就进行改善，一方面引入动量因子、变学习速率等，另一方面采用更有效的数值优化方法，如共轭梯度学习算法、Levenberg-Marquardt算法及B&B算法等，不同的数值优化方法优缺点也差异明显，Levenberg-Marquardt算法是应用于训练BP网络问题的牛顿算法的一个简单版本，其突出优点是收敛速度快，而且收敛误差小[7]。

另外，网络结构的复杂程度，直接影响神经网络训练效率。当网络层次及输入变量节点越多，其计算精度可能越高，但迭代矩阵明显加大，其训练速度越慢，逐步回归-BP神经网络优化算法模型（以下简称混合模型）的思路就是在一定的精度下，首先通过逐步回归法，确定显著性影响因子，减少输入层变量，达到简化网络结构，提高计算效率的效果。

3 实例分析

油罗口水库位于江西省大余县，正常高水位220.00 m，最大坝高36.3 m，为大(2)型水库。主坝为混凝土心墙坝，大坝渗流设3个断面，共14个测压管，采用自动观测监测坝体渗流。选取典型桩号0+144断面，编号依上游往下游分别为UP401、UP402、UP403，其布置见图2，记录时间为2014年1月～2016年12月。

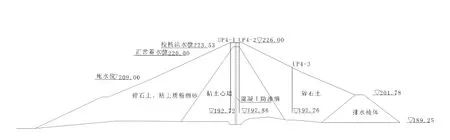
图2 坝体测压管典型断面图

3.1 影响因子分析

综上，水位分量包括上、下游水位差及滞后时间，因此，选取当日至前7日各日上游水位作为影响因素；降雨主要是通过影响上游水位，而间接影响管水位，其过程较为缓慢，但若测压管埋设质量不好，降雨入渗作用明显，也会直接影响管水位，表现为管水位异常升降；时效分量主要由于土体固结沉降作用导致土体的渗透性发生变化；温度因子对土石坝影响较小，可忽略。

分析表明，UP401管水位显著性影响因子为H0及H1，UP402及UP403管水位显著性影响因子均为H1与H3，其中，Hi为i天前的上游水位，降雨及时效等因子均为不显著，计算时可忽略。

3.2 成果分析

采用MATLAB编程，分别进行逐步回归、优化后BP神经网络及混合模型的计算，其中，优化后BP神经网络输入变量采用所有可能影响因子进行分析，混合神经网络(简称混合模型)采用显著性影响因子作为输入变量，其计算结果如下，图3～图5为三种模型拟合值过程线，表1～表3为计算结果拟合精度。

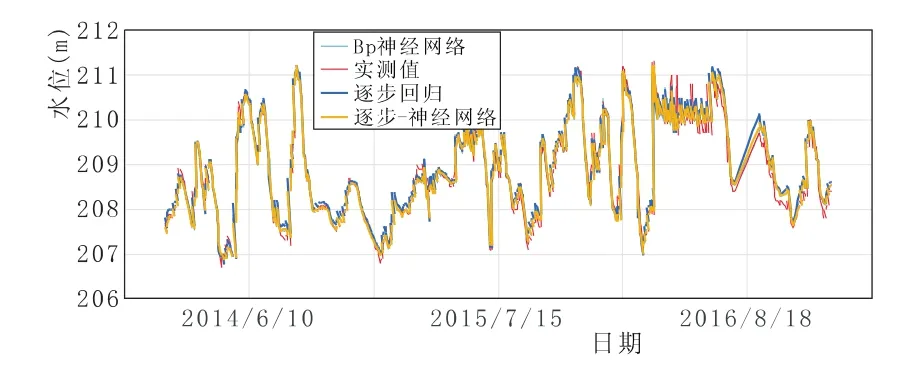
图3 UP401测压管实测水位与回归值过程线

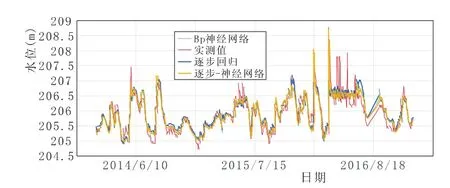
图4 UP402测压管实测水位与回归值过程线

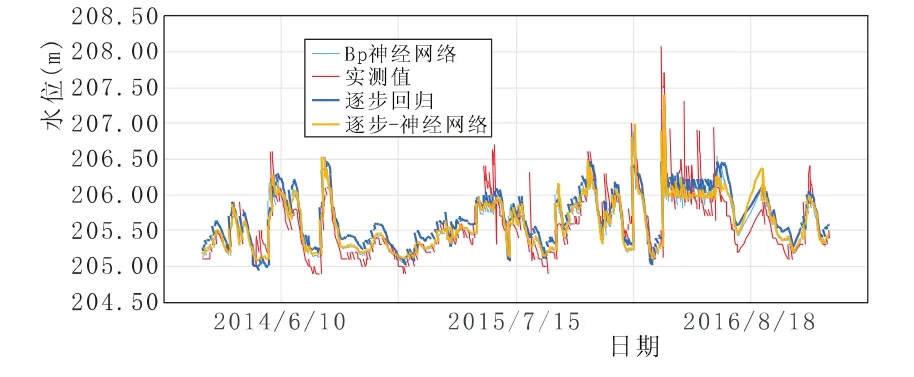
图5 UP403测压管实测水位与回归值过程线

从整体上来讲，三种模型的拟合曲线与原始记录曲线走势较为一致，拟合效果较好。UP401相关系数达到0.98以上，相关性强；UP402相关系数达到0.89以上，相关性较好；UP403相关系数达到0.77以上，相关性一般，表明距上游水位越远，管水位的受影响因素越复杂，如坝基渗流、下游水位等，说明在缺乏相关资料的情况下，采用统计模型进行分析所达到的精度有限。

三种模型中，神经网络的拟合精度较统计模型明显提高，以UP402测压管残差总方差为例，残差总方差为0.21，其次为0.22，最后为0.26，分别较统计模型分别提高31%、23%，表明随着输入层节点增多，拟合效果越好。而且，越往下游，采用神经网络求得的效果越好。

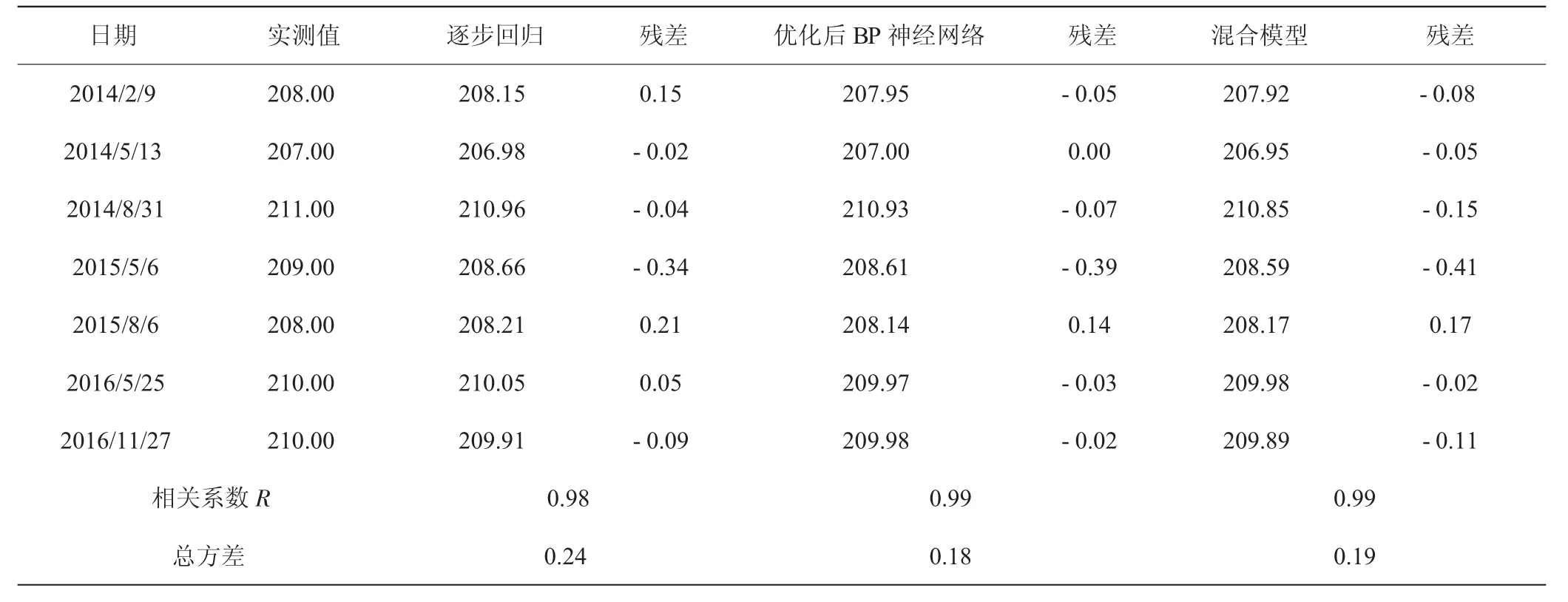
表1 UP401管水位三种模型结果对比

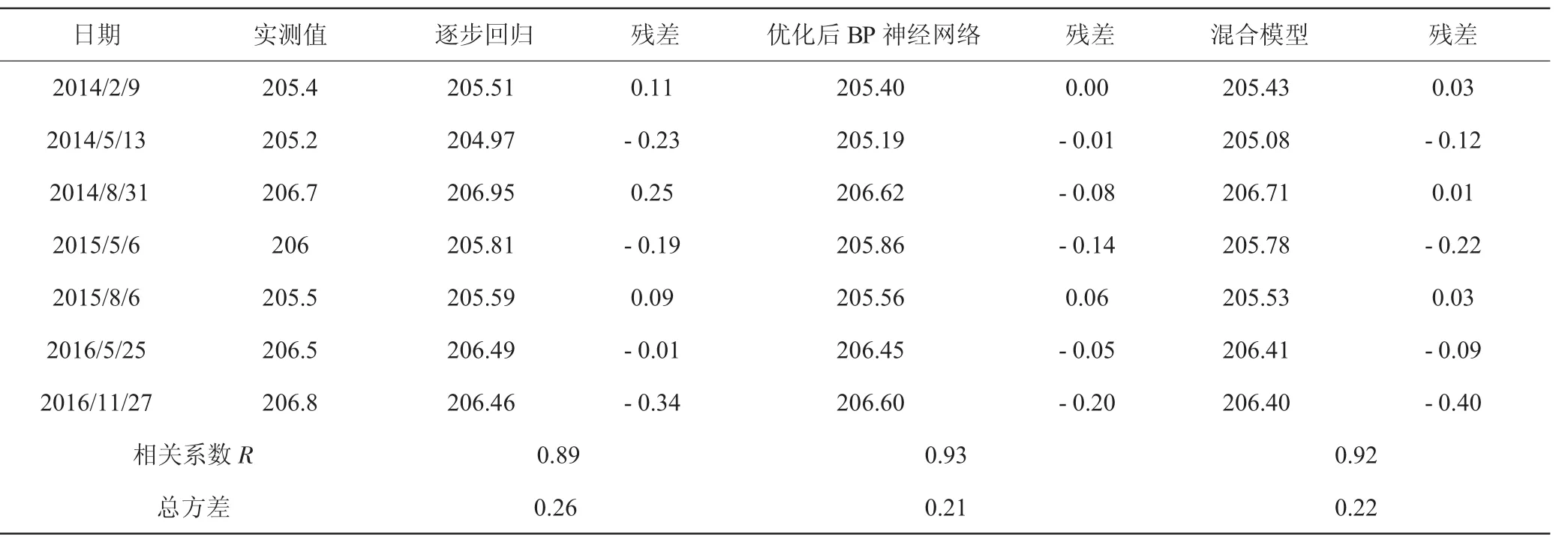
表2 UP402管水位三种模型结果对比

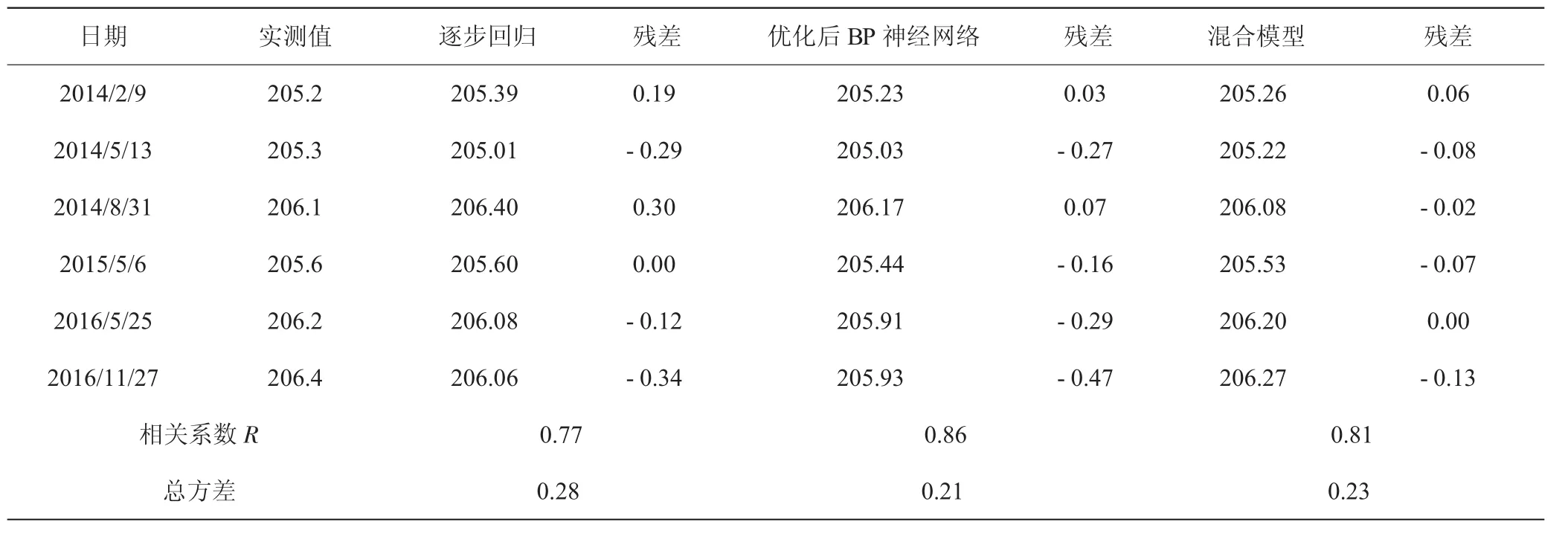
表3 UP403管水位三种模型结果对比

4 结论

(1)对于土石坝心墙上游，采用逐步回归模型及神经网络，拟合精度较高，能达到预测要求。

(2)当位于心墙下游时，逐步回归模型拟合精度下降较快，而采用神经网络模型，拟合效果明显优于逐步回归模型，预测效果最高提高了30%以上。

(3)对于靠近心墙上游测压管，采用统计模型即可达到精度要求，而位于心墙下游，当统计模型精度达不到要求时，可采用神经网络提高预测效果。