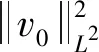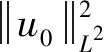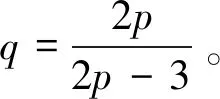三维耗散型电流体动力学系统在齐次Triebel-Lizorkin空间中的BKM型爆破准则*
李秀蓉, 梁洪
(西北农林科技大学理学院,陕西 杨凌 712100)
本文主要研究一类来源于电流体动力学中刻画带电离子漂移、扩散和对流现象的数学模型。该模型中流体的运动由含源项的不可压Navier-Stokes方程刻画, 而带电离子的运动由Poisson-Nernst-Planck方程给出,具有强非线性,奇异性和强耦合性,其三维初值问题如下:
(1)
其中,u=(u1,u2,u3)和π分别表示流体的速度场和压力场,ψ表示电子静电势,v和w分别表示流体中带正电荷和负电荷离子的密度函数。为简单起见,我们已经假设流体密度、粘性系数、电荷迁移率和介电常数均为1。
系统(1)由Rubinstein于20世纪末在文献[1]中首次提出,主要用来刻画等温不可压粘性流体中电场和流场间的相互作用和发展演变原理。2002年,基于Kato半群理论,Jerome在文献[2]中建立了系统(1)局部光滑解的适定性理论。随后,诸多学者考虑了系统(1)在各种初边值条件下的弱解问题,得到了与不可压Navier-Stokes方程类似的一些结果。例如:Schmuck在文献[3]中利用能量不等式和Schauder不动点定理,针对NSPNP系统的Neumann 初边值问题,证明了三维整体弱解的存在性以及若干唯一性和正则性结果。随后,Jerome和Sacco在文献[4]中利用Rothe半离散化方法对NSPNP系统的混合边界问题建立了任意维空间中整体弱解的存在性。Ryham在文献[5]中研究了赋予No-flux边界条件的NSPNP系统初边值问题二维弱解的整体存在性、唯一性和正则性以及三维情形下小稳态解附近整体弱解的存在性。另一方面,对于系统(1)的初值问题,Zhao等在文献[6-8]中建立了其在临界Lebesgue空间、负数阶临界Besov空间和Besov-Triebel-Lizorkin空间中的局部适定性和小初值问题的整体适定性,并建立了自相似解的存在性及其渐近稳定性。特别地,他们还建立了在临界Besov空间中的最优衰减估计。但是注意到,由于Navier-Stokes方程是系统(1)的子系统(此时v=w=ψ=0),所以类似于Navier-Stokes方程,三维情形下系统(1)整体弱解的正则性和唯一性或局部光滑解是否在有限时间发生爆破仍然是电流体动力学中极具挑战性的问题。针对整体弱解的正则性和唯一性问题, Fan等在文献[9-11]和Zhao在文献[12]中分别建立了系统(1)三维整体弱解若干与速度场相关的正则性准则和唯一性准则;Zhao在文献[13]中建立了系统(1)三维整体弱解在齐次Besov空间中与压力场相关的对数型正则性准则。
本文主要考虑系统(1)局部光滑解的爆破问题。最近在文献[14]中,Zhao-Bai建立了系统(1)局部光滑解的BKM型爆破准则和Prodi-Serrin型爆破准则。特别地,他们还建立了如下改进的BKM型爆破准则:若系统(1)的局部光滑解(u,v,w)在时刻T*发生爆破,则一定有
(2)

1 定理的提出

(3)

注1 在定理1的假设条件下,如果对某个时间0 (4) 则局部光滑解(u,v,w)可以延拓至时间T。 注2 在文献[15]中, Dong-Zhang建立了Navier-Stokes方程局部光滑解关于速度场水平分量的爆破准则,即如果 (5) 对于更一般的情形f∈S′(R3),其Fourier变换可由标准的对偶方法来定义,即 ∀ξ∈R3{0} 基于上述φ的构造,令φj(ξ)=φ(2-jξ),h(x)=F-1(φ)(x),其中F-1表示Fourier逆变换。 则对任意的f∈S′(R3),我们定义二进制分解算子Δj和Sj如下: 其中, 最后,我们给出证明定理1需要用到的Bernstein不等式。 引理1[16](Bernstein不等式) 对任意f∈S′(R3),任意非负整数k,任意实数对(p,q)满足1≤p≤q≤∞,存在常数C,有如下不等式成立: 我们利用反证法来证明定理1,即假设(3)不成立,则存在正常数K,有 (6) 基于文献[14]中的定理1.4的证明,为证明定理1,我们只需推导出如下估计: (7) 其中,常数C0仅仅依赖于初值 T和K。 首先,由文献[14]可知,在定理1的假设条件下,带电离子密度函数v,w≥0,且对任意0≤t≤T,有如下的能量不等式成立: (8) (9) ∂3u3=-(∂1u1+∂2u2),ω3=∂1u2-∂2u1 则I1可表示为 于是,我们有 (10) 从而由(10)可得 (11) 为估计I1,一方面,由Biot-Savart定律可知: 其中, 表示Riesz算子。另一方面,由于Riesz算子是L2(R3)上的有界线性算子,因此有下面估计成立: (12) 下面我们估计I1。对I11,由 Hölder不等式,Bernstein不等式和式(12)可推得 (13) 可得 (14) (15) 结合式(13)~(15),我们得到了I1的估计。现将这些估计代入(11),有 (16) 对I2,利用式(1)的第五个方程,能量不等式,Gagliardo-Nirenberg不等式及式(12)可得 (17) 将式(16)和式(17)代入式(9),我们有 (18) 则由(18)可得 (19) 应用Gronwall不等式,我们有 即 从而由(19)可知u∈L∞(0,T;H1(R3))∩L2(0,T;H2(R3)),即式(7)成立。定理1证毕。
2 预备知识




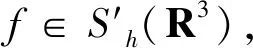
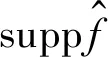
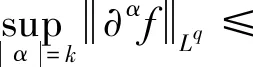
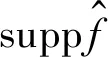
3 定理1的证明