基于人工蜂群算法的交叉口指路标志设置优化方法*

张腾，黄敏，刘芳，郑健

(中山大学智能工程学院∥广东智能交通系统重点实验室，广东 广州 510006)

指路标志是一种交通诱导管理设施，为交通参与者传递道路的相关信息(方向、地点、距离等信息)，指引驾驶员做出合理的路径决策。合理的指路标志系统可以提高交通系统的运行效率，缓解交通拥挤。而实际情况中，指路标志存在信息的缺失、错误以及指引路径不连续等问题，导致出行者错行绕行现象频发[1]。为出行者提供连续的指引信息，帮助其顺利到达目的地是指路标志诱导系统最基本的功能。目前许多学者针对指引信息可达性进行了研究。韩跃杰等[2]建立了指路标志信息连续性评价模型，对路网中的指引信息可达性进行评价。黄敏等[3]结合出行者的寻路习惯，构建了指引信息可达性分析模型，并对指路标志可达性给予了明确的定义与评价。

基于对指路标志系统的可达性评价，优化指引信息是完善指路标志诱导功能、改善道路出行环境的重要举措。有学者提出了相应的指引信息优化方案[4]，把不可达路径扩展为指引可达路径。但，优化方案仅考虑了单条不可达路径的扩展优化，未从整体进行考虑，因此不能满足实际工程的需要。另一方面，车辆路径规划问题是一个NP问题，只有在路网规模较小时才有可能寻求其精确解。因此，启发式算法的应用成为人们研究求解该类问题的重要手段，如：蚁群算法、遗传算法、粒子群算法等[5-8]。但这些算法本身存在一系列问题，如：蚁群算法收敛速度慢、遗传算法易早熟收敛、粒子群算法精度不高且易陷入局部最优等。

人工蜂群算法(artificial bee colony algorithm，ABC)是由Karaboga.D于2005年提出的一种元启发式群智能算法。该算法具有设置参数少、搜索速度快，实现方便等优点，因此其已经被广泛地应用到各个优化领域[9-12]，如：求解旅行商问题、机器人路径规划、通讯领域等，并表现出了强大的适应性和优异性。此前已有学者[4]将人工蜂群算法应用到指引信息的优化问题中，并将实验结果与遗传算法进行了对比。实验表明：人工蜂群算法能比遗传算法更高效地寻找最优路径。本文针对已有的指路标志布设方案，利用可达性分析模型[3]得出了特定兴趣点的多条不可达路径；为将上述多条不可达路径扩展为可达路径，考虑了多条不可达路径扩展时的相互影响，进一步构建出以指引路径与指路标志布设综合最优为目标的优化模型；并利用该模型实现已有指路标志布设方案的优化。实验数据表明：本模型在指路标志优化布设方面具备更好的可行性。

1 指引路径优化问题描述

1.1 路网结构表示

出行者对于路径的选择是基于路网进行的，因此交通路网是路径规划的基础。本文通过“节点-弧段”的方法对路网进行描述，将路网定义为G={V,A}，其中V={vi}为路网G中的节点集合，A={aij|aij=(vi,vj),vi、vj∈V}为G中的弧段集合，aij为有向路段vi到vj，cij为弧段aij的弧段信息，如路段长度信息。

1.2 指引路径与指引可达

指引路径是驾驶员根据指路标志系统的指引和驾驶员自身驾驶经验的指导，选择出的一条从起点前往指定终点的期望路径。在驾驶过程中，驾驶员会根据指路标志给出的指引信息进行路径选择。当道路交叉口缺少对目的地指引的指路标志时，驾驶员会根据自己的驾驶经验做出选择。

基于已有的指引信息可达性分析模型，本文对指引信息构成的指引路径进行分类和定义。已知某路网，路网结构如图1所示。当指引路径能够实现驾驶员从起点到终点的出行，就称这条指引路径是指引可达的，即O1出发路径；反之，则称这条指引路径是指引不可达的，即O2出发路径。

1.3 指引路径的综合优化问题

决策者在规划指引路径的过程中，需要综合考虑多方面因素，如：指引路径的长度、增设指引信息的数量、道路的重要程度等。

已有的单条路径优化模型[4]以指引路径长度和增设指路标志数量综合最优为目标，把单条不可达路径扩展为指引可达路径。然而，工程实际中可能出现多条不可达路径，如果将它们单独优化，并把结果进行直接叠加，所得的最终路径可能非最优。

图2 指引路径单独优化示意图Fig.2 Single optimization guide path

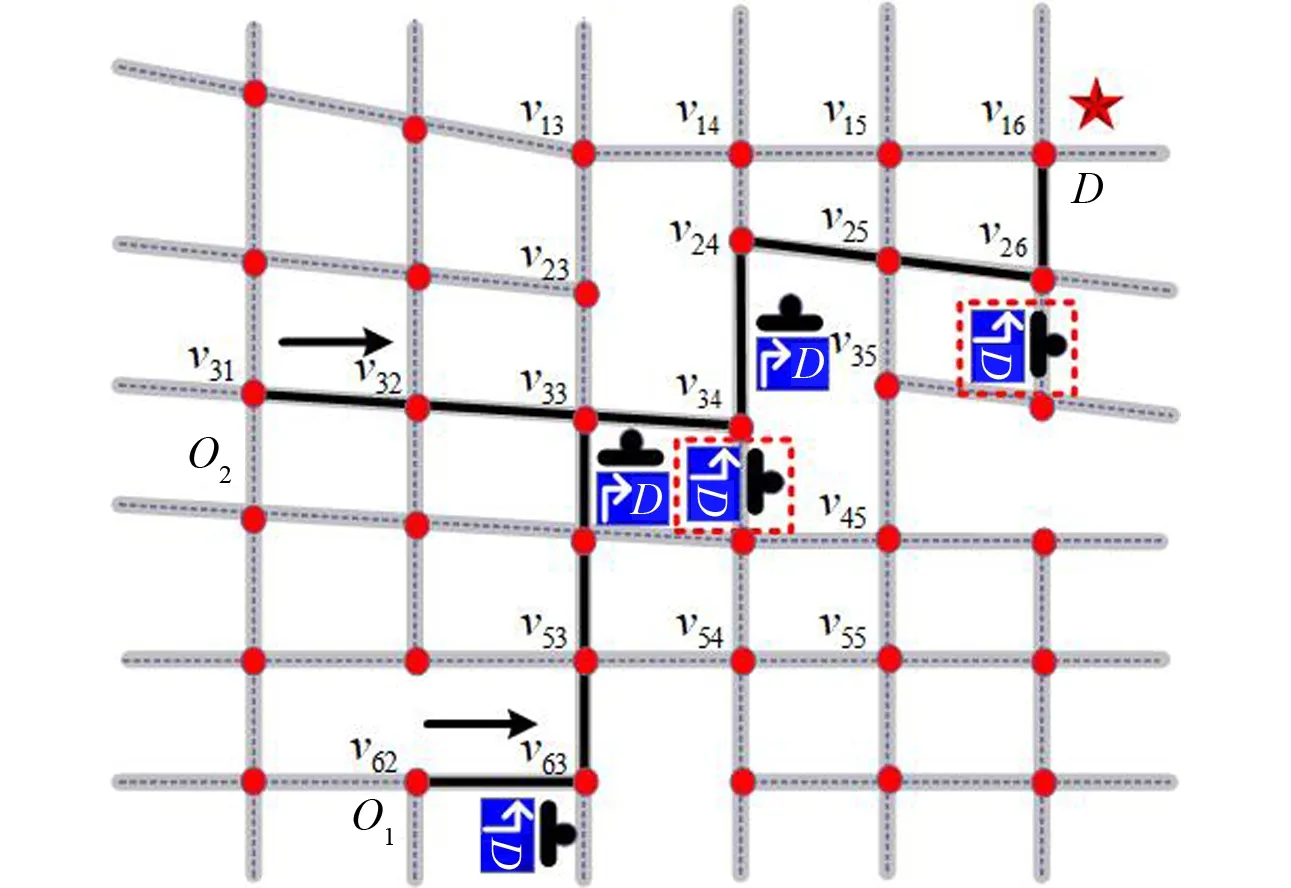
图3 指引路径综合优化示意图Fig.3 Guide path overall optimization

如图2路网中，已知O1、O2为D的两条不可达路径端点，且路网中已有指向D的指引信息(图中虚线框内为已有指引信息，下同)，对其分别进行优化，得到的优化路径如图2所示。但若对两条不可达路径进行综合优化，可得如图3所示路径。综合优化考虑到了对重复指引信息的利用，两条路径在v33处合流后，路径可共用同一指引信息，如：v34、v26处共用已有指引信息，v24处共用新设指引信息，需增设指引信息要少于单独优化路径，因此综合考虑此路径可能优于单独优化路径。

为了使系统的整体可达性达到最优，需将多个单条扩展路径看成一个整体进行综合优化。

1.4 指引路径的综合优化模型

假定路网结构G已知，对给定的被标识对象D，其指引信息集合RS={rs}，设D共有n条不可达路径x1,x2,,xn。则对于每条不可达路径xi，从其端点Oi开始扩展，直至到达D，该延伸指引路径分段记为ei，记e={e1,e2,,en}为D的一条延伸指引路径。如图2所示，e={e1,e2}即为D的一条延伸指引路径。其中，e1为起点O1到终点D的路径，e2为起点O2到终点D的路径。E={e}为D的所有可能延伸指引路径的集合。指路标志的综合优化模型需综合考虑指引路径长度和增设指路标志数量两个要素。但二者的数量单位不统一，因此需要进行归一化处理。在已知指引路径的长度、已设置指路标志数量的前提下，本文利用最大距离d和最大数量N，实现了对指引路径长度和指路标志设置数量的归一化处理。

综上所述，指引路径的综合优化模型如公式(1)所示。目标函数通过对指引路径长度和增设指路标志数量的归一化处理，使得模型可通过目标函数值实现对整体优化方案的优劣评价，且目标函数f值越小，指引路径越优。

s.t.RS (ei)∩RS (ej) = ∅,∀ei,ej∈e

RS (ei)∩RS= ∅,∀ei∈e

(1)

其中， leni为延伸指引路径分段ei的长度， numi为ei中需增设的指引信息个数，RS (ei)为ei中需增设的指引信息集合，α1表示路径长度对决策的重要程度占比，α2表示增设指引信息对决策的重要程度占比。

2 指引路径优化问题的人工蜂群算法

求解指引路径优化问题的关键在于综合考虑延伸指引路径的路径长度及增设指引信息数量，使得延伸指引路径的总评价指数最优。结合人工蜂群算法的基本特点，本文设计了一种人工蜂群算法用于求解该优化问题。

2.1 延伸指引路径表达方式

本文将单条延伸指引路径e定义为单个蜜源，并记录为e={ei|i=1,2,···,n}，其中n为延伸指引路径中分段数。假设延伸指引路径分段ei从Oi点出发，依次经过vp(i)、、vq(i)等点，到达D点，则记录e为

其中，tj表示该路径经过节点vj处是否需要增设指引信息。若需要，则tj=1；反之，则tj=0。

根据前人的研究[15]，在缺少指引信息的路口，绝大多数驾驶员会选择直行。为简化算法表达，本文仅在延伸指引路径转弯处增设指引信息。

如图4所示路网，存在两条不可达路径，端点分别为O1、O2，目的地为D，且在v26处已有指向D的左转指引信息。则图4中黑线为一条延伸指引路径e={e1,e2}，并在转弯处增设指引信息，该路径e的编码为

其中，e2经过点v25时，此处已有e1增设指引信息，不需重复增设，因此e2中t25=0。

图4 延伸指引路径示意图Fig.4 The extended guidance path

2.2 适应度函数

根据1.4中对目标函数的分析，延伸指引路径e的优劣程度由适应度F判断。路径适应度F由式(2)求得，适应度函数值越小，指引路径越优。

(2)

2.3 算法整体流程

人工蜂群算法的整体流程如图5所示。

图5 算法流程图Fig.5 Procedure of algorithm

其对延伸指引路径的更新分为引领蜂、观察蜂及侦察蜂三个阶段进行，计算步骤如下：

(1)初始迭代次数cycle= 1，并初始化蜜源种群R={ek|ek∈E,k= 1,2,···,SN }，其中SN为蜜源种群规模。

(2)引领蜂k对延伸指引路径ek采用邻域搜索策略进行更新，k=1,2,,SN。

(3)观察蜂k依据概率随机选择一条路径，并采用邻域搜索策略对所选路径ei进行更新，选中路径ei的概率Pi由式(3)求得：

(3)

其中，Fi为路径ei的适应度，k=1,2,,SN,i∈{1,2,,SN}。

(4)令单条路径最大连续搜索数为limit，对ek连续搜索次数进行判断，若连续搜索次数超过limit路径ek仍未发生变化，则视为陷入局部最优，舍弃该条路径，由侦察蜂重新生成新的ek，k=1,2,,SN。

(5)将当代所有指引路径ek与历史最优指引路径eopt的适应度进行比较，更新最优指引路径eopt。

(6)令算法的最大优化代数为MEN，若cycle=MEN，算法终止，最优路径为eopt；反之，cycle=cycle+1，返回步骤(2)，继续优化。

2.4 延伸指引路径更新策略

由2.3中的整体流程可知，算法更新路径主要采用邻域搜索策略，但实际路网结构复杂，路径之间的邻近关系不规则，无法直接采用函数优化中构造邻域的方法，因此本文设计了一种适应于路网结构的邻域搜索策略，以实现指引路径的更新，其更新操作如下所示：

(1)计算路径e={ei}的适应度F，并将其分解为n条分路径ei，移除所有增设指引信息。

(2)为分路径ei搜索邻域分路径，令i=1。

(3)随机选取路径ei上两点作为邻域段的起点和终点。

(4)删除邻域段内节点，重新选取该段路径，用新生成路段补全邻域段。

(5)按规则添加指引信息，并对路径重新编码，生成ei的邻域分路径ei′。

(6)若i=n，转步骤(7)；反之，i=i+1，转步骤 (3)。

(7)将邻域路径ei′整合为e的邻域路径e′={ei′}，计算其适应度F′，并与F比较，保留更优路径。

以图4所示延伸指引路径e={e1,e2}为例，e1选取v63为邻域起点、v35为邻域终点，重新选取新路段组成邻域分路径e1′，并增设指引信息，如图6(a)所示；e2选取v32为邻域起点、v35为邻域终点，重新选取新路段组成邻域分路径e2′，并增设指引信息，如图6(b)所示；将两条邻域分路段进行整合，组成邻域路径e′，如图6(c)所示。由于F′

图6 指引路径邻域搜索过程图Fig.6 Guide path neighborhood search process graph

3 实例应用

选择广州大学城路网作为试验路网，路网总共包括333个节点，812条路段。利用已有可达性分析模型[3]分析，A、B、C三处都是中山大学的指引不可达路径端点，其中A为华南快速路出口，C为交叉口，B为道路入口，已有指引信息如图7所示。因此，选择点A、B、C作为延伸指引路径的起点，点D中山大学作为终点，对指引路径进行综合优化。本实验认为路径长度、增设标志数对选择的贡献值相同，因此取α1=50%，α2=50%。同时根据多次试验确定了模型的参数为SN=100，MEN=200，limit=200，并借助 ArcGis 10.0 平台进行了实验仿真，程序采用C#编程语言实现。

对图7运用指引路径优化模型，可得到如图8所示结果。其中路径总长度为11 510.99 m，总共需要增设的指引信息数为6个，计算得到的适应度值为1.196 409。

在相同条件下，运用单条路径优化模型分别对各个起点寻找最优路径，其各条路径寻优结果如图9所示，路径信息如表1所示。将其直接叠加，可得到如图9(d)所示结果。其中，路径总长度为11 499.99 m，各条路径的指引信息数之和为8个，其中有两个为相同指引信息，舍弃重复信息，因此需要设置的指引信息数为7个，计算得到的其适应度值为1.273 985。

图7 广州大学城路网Fig.7 Guangzhou University city road network

图8 算法优化结果Fig.8 Algorithm optimization results

最优路径指引路径的距离/m需设指引信息数/个适应度FA→D优化4 675.87830.435 070 4B→D优化2 712.35330.582 804 6C→D优化4 111.75520.390 283 4

指引路径综合优化模型、单条路径优化模型的计算结果如表2所示。通过对比可发现，综合优化模型得出的路径适应度更低，结果更优。由此可见，综合优化模型在整体性考虑方面更优，更符合实际需求。图10为算法的收敛曲线。可以看出，迭代至140次左右时适应度已收敛至全局最小值。

表2 结果数据对比Table 2 Results by different methods

图9 单条路径优化结果示意图Fig.9 Single path optimization results

图10 算法收敛曲线Fig.10 Algorithm convergence curve

4 总 结

本文探讨了人工蜂群算法在指引路径综合优化中的应用，提出了一种适应路网结构的邻域搜索策略，并综合考虑路径的长度、设置指引信息数两项指标，初步构建了相应的优化模型，并将其运用于实际路网。实验证明：指引路径综合优化模型具有可行性和良好的适用性，且相较于单条路径优化模型，更符合实际需求。但，目前模型只考虑了单个指引对象，当存在多个指引对象时，指引路径间会相互影响，还会出现过载现象，且模型在优化过程中考虑的影响因素等方面仍有深入研究的价值，后续研究中将会进一步扩大优化考虑范围，提高模型的实际应用性。