交叉结构面对岩体力学特性的弱化效应*

刘佳明，孙少锐，张中行，高林，苏运基

(1.中国电建集团海南电力设计研究院有限公司，海南 海口570100； 2.河海大学地球科学与工程学院，江苏 南京 210098)

裂隙岩体广泛存在于岩体工程中，其强度、变形和破坏形式均对岩体工程的施工及运营期的稳定性有重要影响。目前，对于裂隙岩体的强度分析大多采用单结构面弱化理论及其的推广理论。单结构面弱化理论由Jaeger(1960)提出，并广泛应用于岩土力学的解析和数值计算中，作为裂隙岩体的破坏判据。该理论假设存在两种相互独立的破坏方式：沿断续面滑动破坏和完整岩块的剪切破裂，破坏方式由断续面走向和主应力方向夹角决定。Hoek和Brown[1](1980)将单条结构面弱化理论推广到多条结构面条件下的岩体强度分析，其中各条结构面之间的夹角是相同的。继而，可以推断出：在包含四组或更多组结构面的岩体中，其强度是接近于各向同性特征的。韩建新等[2]利用单结构面理论分析了不同结构面组合条件下岩体试样的破坏形式，未考虑交叉结构面间的相互作用和应力路径对岩体力学性质的影响。通过室内类岩石材料模型试验[3-6]，有学者针对单一结构面、多条平行结构面和含两条正交结构面裂隙的岩体的力学行为进行了研究，得到了一些有价值的成果，但均未考虑结构面间的相互作用。Halakatevakis和Sofianos[7](2010)将单条结构面弱化理论推广到任意多条贯穿断裂面、各条结构面的单独分析，并取低值作为低强度包络线。但，与室内试验数据对比，可以发现：在低围压条件下，该方法对岩体强度估计过高；在较高围压条件下，所得到的结果与实验数据相近。因模型制作困难，Kulatilake[8]等采用相似材料和颗粒流方法(PFC2D)研究了包含两条交叉结构面的岩体试样的强度、变形和破坏特征，并提出了试样的单轴抗压强度与结构张量之间的关系。黄彦华[9]采用PFC2D模拟了包含两组交叉结构面的砂岩试样的单轴和三轴压缩试验，并观察到裂隙试样的五种破坏形式：张性破坏、沿节理滑移破坏、穿节理剪切破坏、张性滑移破坏和剪切滑移破坏。刘佳明等[10]对裂隙岩体试样进行了单轴压缩试验，研究发现：裂隙岩体的强度不仅仅取决于最不利结构面；Jaeger的单弱面理论在包含两组倾角相近的交叉结构面的岩体中不适用。另外一些研究者的室内试验[11-12]也证明了单弱面理论在多裂隙岩体的强度分析中的不适用性。

交叉结构面是岩体中结构面的主要赋存形式之一。但，目前对包含交叉结构面的岩体的强度、变形和破坏特征的研究，大部分仅考虑了单一结构面、平行分布多条结构面的情况，仅少数研究人员对X型交叉裂隙岩体的力学行为进行了研究。而，对于交叉结构面的相互作用及其对岩体力学特性的弱化效应，目前少有相关文献发表。本文通过颗粒流方法(PFC3D)，以裂隙倾角、倾角组合为变量生成了多裂隙圆柱试样；并对试样进行单轴压缩试验，得到了含交叉结构面的岩体的力学性能，包括应力场、起裂及破坏形式等的规律。研究结果为岩体稳定性评价、岩体工程的设计、施工提供了一定的理论基础。

1 试验设计

参考文献[10]中完整试样和结构面的力学性质，并考虑单裂隙试样中结构面倾角对试样破坏形式的影响，将结构面倾角分为三个区间：①张性破坏，0°～25°和80°～90°的倾角；②沿结构面破坏，35°～80°的倾角；③混合破坏模式，25°～35°的倾角。针对三个区间进行试验设计，考虑相同和不同区间组合分别进行单轴压缩和三轴压缩试验，试验方案如表1所示。假设两条交叉结构面的倾角分别为β1与β2，其模型如图1所示。

表1 试验设计方案Table 1 Design scheme of experiment

图1 包含交叉结构面的模型示意图Fig.1 Model of jointed sample with two sets of crossed joints

丁晓兵等[13]基于大量数值模型的尺寸效应研究，给出：在2%的容差范围内L/d的比例至少为25，其中L为最小边长(圆柱试样中取直径)，d为颗粒平均直径；且还需满足国际岩石力学学会关于L/dmax≥20的要求。考虑计算效率和消除尺寸效应，本文的L/d取为31.25。Rmin和Rmax分别为0.8 mm和1.6 mm，颗粒粒径在Rmin～Rmax之间随机分布。依据以上尺寸生成50 mm ×100 mm的圆柱试样，每个模型中包含22 450个颗粒。张小平等[14]采用PFC3D模拟了0.016～0.200 m/s的加载速度条件下岩体试样的单轴压缩试验；并与加载速度为0.5～0.8 m/s条件下岩体试样的室内单轴压缩试验进行了对比，研究发现：加载速率过小时，数值模拟与室内试验结果差异较大。因此，本文采用的轴向加载速度为0.05 m/s。

为避免结构面贯穿试样顶底面对试验结果产生干扰，仅考虑倾角为10°～60°的结构面对岩体强度的影响。同时，对单裂隙试样、双裂隙等倾角试样以及双裂隙不等倾角试样进行单轴压缩试验，从裂隙发展、应力场的角度出发，分析交叉结构面对试样强度的影响。

2 裂隙岩体单轴数值试验

2.1 岩石和结构面细观参数标定

岩体试样采用文献[10]中的相似材料试样，建立完整的岩石试样模型和直剪试样模型。PFC3D中需要的参数为表征颗粒和联结的细观参数，包括几何参数、细观力学参数。其中，几何参数包括模型的长宽高、颗粒的最大粒径、最小粒径和孔隙率。如果选择的联结模型为平行联结模型，几何参数还包括平行联结的半径乘子。颗粒的力学参数包括颗粒的密度、法向刚度、切向刚度和颗粒间的摩擦系数。平行联结的力学参数包括其法向刚度、切向刚度、法向强度、法向强度的误差、切向强度和切向强度的误差。诸多学者[14-16]结合室内试验和数值模拟结果，得出了一些颗粒的细观参数和材料宏观参数之间的联系。然而，材料的某一宏观参数与多个数值模型的细观参数相关，细观参数对宏观参数的影响也不是单一对应关系。因此，在应用PFC3D进行模拟前，需要根据材料的实际参数进行严谨的参数校准工作。

本文中岩体试样均采用平直结构面，不考虑结构面的粗糙度影响。通过试错法模拟岩体试样的单轴压缩试验和直剪试验，得到与实际相符的抗压强度、弹性模量和泊松比，标定相应的颗粒和联结的细观参数。表2为完整岩块和结构面的细观参数，表3为室内试验与数值模拟结果对比。在表3中，数值模拟得到的宏观力学参数与室内试验的结果十分接近，误差较小。因此，用数值模拟校准的细观参数基本可以代表完整岩石材料和结构面的真实力学性质，可以采用表2中的细观参数来开展裂隙岩体的单轴压缩数值模拟。

表2 岩石和结构面的细观参数Table 2 Microscopic parameters of rock and joint

表3 室内试验与数值模拟的宏观力学参数对比Table 3 Comparison of material properties of physical experiment and numerical simulation

在完成岩块和结构面的细观参数校准后，生成与室内试验尺寸一致的圆柱形模型，同时根据试验方案生成不同结构面组合的裂隙岩体模型。为验证所校准微观参数的可靠性，还要对比数值模拟与室内试验结果的一致性。取试样S-10、S-30、SD-30和SD-40，由于PFC3D程序中颗粒生成的随机性，对试样的6个数值模型进行单轴压缩模拟实验，取其单轴强度和变形模量均值与室内试验结果进行对比，如表4所示。从表4所示结果可以看出，数值模拟与室内试验的结果表现出良好的一致性，说明上文校准的颗粒和接触细观参数能够较为准确地表现裂隙岩体的宏观力学特性。

表4 室内试验与数值试验结果对比Table 4 Comparison of physical and numerical tests results

室内试样和数值模拟模型的典型破坏形式如图2所示。其中，数值模拟模型的黑色短柱表示接触力链，灰白色和灰褐色圆点分别表示张拉破坏和剪切破坏形成的微裂纹，裂纹相互连接形成的贯穿面即为岩体的破坏面，可以明显看出试样S-10的破坏形式为典型的张性破坏，试样SD-30和SD-40的破坏形式为沿结构面剪切破坏，而试样S-30的破坏形式为混合破坏形式，数值模拟模型的破坏形式与室内试验相吻合。

2.2 单裂隙试样与双裂隙等倾角试样对比

本节对单裂隙试样与等倾角双裂隙试样在单轴压缩作用下的表现进行研究，分析等倾角交叉的结构面对试样的变形特征、强度特征、微裂纹发展、应力场和破坏形式的影响。单裂隙试样和双裂隙等倾角试样的单轴试验应力-应变关系如图3所示。试样S-10和SD-10的强度分别为38.19 MPa和32.47 MPa，试样S-20和SD-20的强度分别为36.46 MPa和30.71 MPa，试样S-30和SD-30的强度分别为32.00 MPa和27.12 MPa。可以明显看出，当结构面倾角在10°～30°间时，等倾角交叉结构面之间的相互作用对试样的强度有明显的弱化影响。从峰值应变来看，双裂隙模型的峰值轴向应变也明显小于单裂隙试样。20°和30°分别在区间①和②内，故可推断：对区间①内的小倾角和区间②内的所有倾角而言，等倾角交叉结构面的相互作用对岩体的强度有明显的弱化影响。而，当结构面倾角在40°～60°时，等倾角交叉的双裂隙试样的单轴抗压强度与同倾角的单裂隙试样相比也有一定程度的相对弱化，由于在此区间内裂隙试样的强度较低，故其强度差绝对值较小；在倾角为40°、50°和60°时，其单裂隙模型与双裂隙等倾角试样的强度差分别为1.07 MPa、1.22 MPa和1.62 MPa。同时，随着结构面倾角的增大，岩体的抗压强度有显著降低的趋势，这是由于随着倾角的增大，轴向荷载在结构面上的法向应力分量逐渐减小且切向应力分量逐渐增大，故而导致单轴抗压强度随倾角的增大而逐渐降低。

图2 室内模型和数值模型的典型破坏形式Fig.2 Typical failure modes of physical and numerical tests

图3 单裂隙模型与等倾角双裂隙模型在单轴荷载下的应力-应变曲线Fig.3 Comparison of the stresS-strain curves under unaxial compression between the single joint model and double joint model with same dip angles

现根据应力场分布来研究交叉结构面相互作用对试样强度的弱化机制。取与轴向平行、与结构面走向垂直且过试样中心的平面为纵剖面，向两侧各扩展0.1 mm，取该方形区域内的接触作为取样点。在0.25σc、0.5σc、0.75σc和σc时，导出试样纵剖面内颗粒间平行接触的法向应力和剪应力，在Originlab中分别作出试样SD-30和S-30的应力云图，同时导出不同应力条件下时试样的接触力链图，如图4所示。试样中微裂纹总数量与轴向应力的对应关系，如图5所示。需要指出的是，在PFC3D颗粒流模型中，颗粒间的平行联结有法向抗拉强度和切向抗剪强度。当平行联结上的法向应力超过其抗拉强度或其剪应力超过其抗剪强度时，平行联结将发生破坏且不再继续承载和传递应力。

图4 模型S-30与SD-30在不同轴向应力下的应力云图与接触力链Fig.4 Stress contour and contact force chain under different axial stress for model S-30 and SD-30

从图4可以看出，当轴向应力达到0.25σc时，模型S-30与SD-30的法向应力分布基本一致，都是沿着结构面呈张应力集中分布。其中，SD-30中在结构面交叉处有明显的应力集中，其应力水平较低，远低于试样的接触法向强度。且，SD-30的应力水平也较低，可以看出应力主要沿结构面附近的接触集中分布，应力集中带呈X型分布。

当轴向应力达到0.5σc时，模型S-30和SD-30的法向应力成倍增大；此时S-30中尚未发生平行联结的破坏，而SD-30中已有14个平行联结的张性破坏产生，这是由结构面交叉处的应力集中所导致；在图4中，由于采样点接触的破坏，导致SD-30此时没有明显的应力集中表现，且因平行联结的剪应力强度较法向强度要高，故此时没有发生平行联结的剪切破坏，接触力链图也基本与上一阶段一致。

当轴向应力达到0.75σc时，由图5可以看出，此时S-30和SD-30中均产生了一定数量的微裂纹。而相同的轴向应力条件下，SD-30中的微裂纹数量明显多于模型S-30。由于采样点接触的破坏，此时的张应力最大值相对于0.5σc时并未成比例上升。从接触力链图上看，此时二者的应力集中带仍然沿结构面分布。

在轴向应力达到σc时，张应力和剪应力最大值分别接近平行接触的法向强度和切向强度均值。即，随着荷载继续增加，应力集中部位的接触将会发生相应的剪切破坏或张性破坏。由应力云图的分布可以看出，在S-30的截面上，张应力主要沿30°结构面集中分布，但也在完整材料中有一定的分布，其集中分布带与结构面小角度相交。而在SD-30的截面上，应力集中带主要沿结构面分布，应力集中在完整材料部分的分布较S-30有明显减少，这是由于此时SD-30的应力低于S-30。同样，通过接触力链图可以看出，在接近峰值时，模型S-30的应力除沿结构面分布外，还有向岩块部分扩展，而SD-30的应力依然只沿结构面分布。

S-30与SD-30峰值时的应变分别为1.73×10-3和1.62×10-3，前者在峰值应力时的应变和微裂纹数量均大于后者，两者平行联结的破坏总数量分别为1 156和993个。可以明显看出，SD-30的平行联结发生破坏时的应力明显低于S-30的，且在峰值前SD-30的微裂纹数量显著高于模型S-30的，这也导致在较低的轴向应力条件下SD-30中的微裂纹相互连接形成贯穿的宏观破坏带，即SD-30在相对较低的应力条件下就会发生破坏。

当结构面倾角为20°或60°时，单裂隙试样与双裂隙等倾角试样在0.5σc时的应力云图，如图6所示。根据微裂纹总数量与轴向应力关系曲线可以看出，在0.5σc时，处于裂隙初始扩展阶段，仅有少量的微裂纹产生，此时的应力分布可以在一定程度上反映整个压缩试验中试样的应力场。从图6可以发现，与单裂隙试样相比，等倾角双裂隙试样在裂隙交叉处均有一定的应力集中表现。

当结构面倾角为20°或60°时，单裂隙与等倾角双裂隙试样的微裂纹总数量与轴向应力的关系，如图7所示。由图7可以看出，对于结构面倾角为20°和60°的试样，单裂隙与等倾角双裂隙试样的微裂纹数量与轴向应力的关系有明显的差异，即交叉结构面对试样在单轴作用下微裂纹的扩展有明显的影响。等倾角双裂隙试样的起裂应力要显著小于单裂隙试样，并且微裂纹总数量明显大于单裂隙试样中的微裂纹总数量。同时，随着结构面倾角增大，峰值时微裂纹数量有逐渐减小的趋势，这是因为：随着结构面倾角的增大，岩体的峰值应力逐渐降低，在较低的轴向应力作用下发生破坏的接触较少，并且岩体的破坏形式也逐渐由岩块的张性破坏转变为沿结构面剪切破坏。

微裂纹总数量达到峰值时微裂纹总量的10%时的轴向应力为起裂应力σci。起裂应力从微裂纹发育和扩展的角度反映了结构面对裂隙试样的弱化作用。单裂隙与等倾角双裂隙试样在单轴压缩作用下的起裂应力，如表5所示。

图5 试样S-30与SD-30 中微裂纹总数量-轴向应力曲线Fig.5 The curves of total cracks number to axial stress for model S-30 and SD-30

图6 单裂隙试样与双裂隙等倾角试样在 0.5σc时的应力云图Fig.6 Stress contour of the single joint specimens and double joint specimens with same dip angles under 0.5σc

图7 单裂隙与等倾角双裂隙试样的微裂纹总数量-轴向应力曲线Fig.7 The curves of total cracks number to axial stress of the single joint specimens and double joint specimens with same dip angles

表5 单裂隙与等倾角双裂隙试样的起裂应力Table 5 The crack initiation stress of the single joint specimens and double joint specimens with same dip angles

从表5可以看出，等倾角双裂隙试样的起裂应力低于单裂隙试样，这是由于前者的结构面交叉处在较低的轴向应力下产生了微裂纹。双裂隙试样在相同的轴向应力下的微裂纹发育程度高于单裂隙试样，进一步导致了等倾角双裂隙试样在较低强度下形成贯穿的破坏面。单裂隙试样与等倾角双裂隙试样在单轴压缩作用下的破坏形式如图8所示。

从图8可以看出，在区间①内，当结构面倾角为10°时，交叉结构面对裂隙试样的破坏形式没有明显的影响，其破坏形式均为完整岩块的张性破坏；随着结构面倾角增大，当结构面倾角为20°时，单裂隙试样的破坏模式为完整岩块的张性破坏，而等倾角双裂隙试样的破坏形式变为混合破坏模式。这表明当结构面倾角较小时，交叉结构面对裂隙试样的破坏形式没有明显影响；而，当结构面倾角较大(接近区间③时)，等倾角双裂隙试样的破坏形式由张性破坏变为混合破坏模式。当结构面倾角为30°时(在区间③内)，等倾角交叉结构面对试样的破坏形式有明显的影响，单裂隙试样为混合破坏模式，而等倾角双裂隙试样的破坏形式变为沿结构面滑移破坏。当结构面倾角在区间②内时，交叉结构面对试样的破坏形式没有明显的影响，单裂隙和等倾角双裂隙试样的破坏形式均为沿结构面发生破坏。选取试样S-10、S-30与S-60分别代表张性破坏、混合破坏、沿结构面滑移破坏三种破坏形式，现分析试样的微裂纹数量与轴向应变的关系、应力-应变曲线，如图9所示。值得注意的是，各试样均运行到峰值后的0.6倍峰值应力时。

图8 单裂隙与等倾角双裂隙试样的破坏形式Fig.8 Failure mode of the single joint specimens and double joint specimens with same dip angles

图9 试样的微裂纹数量-应变和应力-应变曲线Fig.9 The cracks number-strain curve and stress-strain curve of specimens

从图9可以看出，不同破坏形式所对应的平行联结破坏趋势存在较大差异。其中，完整岩块张性破坏的微裂纹数量显著多于其他破坏形式的，在峰值时为1 453个，在峰值后的0.6倍峰值时增长到7 305个。在图9(a)中，微裂纹的数量在峰值后逐渐增大，且其增长速度呈增大趋势。混合破坏形式的微裂纹数量在峰值时为1 017个，在峰值后的0.6倍峰值时达到4 205个，其破坏的增长趋势与完整材料的张性破坏相似。如图9(b)所示，混合破坏形式的张性微裂纹和剪性微裂纹的增长速度低于完整岩块张性破坏的增长速度。在图9(c)中，沿结构面滑移破坏的微裂纹数量较完整岩块张性破坏的要小一个数量级，在峰值后的0.6倍峰值时的平行联结总数量为609个；且在峰值之后，平行联结破坏的增长速度呈降低的趋势，在峰值后的0.6倍峰值时，其增长速度趋近于零。

2.3 单裂隙试样与非等倾角双裂隙试样对比

单裂隙(S组)和非等倾角交叉结构面试样(SN组)在单轴作用下的应力-应变曲线如图10所示。由图10可以看出，除试样SN-1(20°和30°)的强度显著小于S-20和S-30外，其他SN组试样的单轴抗压强度均与单裂隙试样的相近，且其峰值的轴向应变也基本相同。即，交叉结构面的相互作用仅对SN-1试样的强度起了弱化作用，而其他双裂隙试样的强度主要由倾角较大的结构面控制。

图10 单裂隙与双裂隙非等倾角试样的应力-应变曲线Fig.10 Stress-strain curve of the single joint specimens and double joint specimens with different dip angles

S-30、SN-1和SD-30(最不利结构面的倾角均为30°)在轴向应力达到其峰值应力的0.5倍时的应力云图，如图11所示。从图11可以看出，当轴向应力均处于0.5σc时，SN-1与SD-30的应力分布较相似，均在结构面交叉处出现明显的应力集中现象；S-30沿着结构面上有3处明显的应力集中，但在结构面交叉处没有明显的应力集中表现。S-30、SN-1和SD-30的最大拉应力分别为24.8 MPa、22.6 MPa和24.7 MPa，此时的轴向应力分别为16 MPa、13.88 MPa和13.56 MPa，将最大拉应力与轴向应力的比值定义为法向应力集中系数Kn，则S-30、SN-1和SD-30的Kn分别为1.55、1.63和1.82，即SD-30的应力集中程度最高。三个试样的微裂纹数量与轴向应力的关系，如图12所示。可以看出，在微裂纹扩展的初始阶段，裂隙扩展的速度从大到小依次为SD-30、SN-1、S-30。

图11 轴向应力为0.5σc时S-30、SN-1与SD-30的应力云图Fig.11 The stress contour under 0.5σcfor model S-30, SN-1 and SD-30

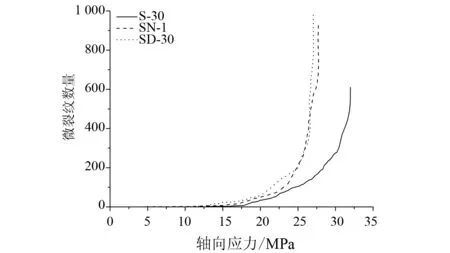
图12 S-30、SN-1与SD-30的微裂纹数量-轴向应力曲线Fig.12 The curves of total cracks number to axial stress for model S-30, SN-1 and SD-30

在图12中，在微裂纹的起裂阶段，相同轴向应力条件下SN-1的微裂纹数量大于S-30，但小于SD-30。随着轴向荷载的增加，SN-1中的微裂纹数量和扩展速度与SD-30逐渐接近；当轴向应力接近峰值时，二者的微裂纹数量和扩展速度基本一致。并且，二者的微裂纹数量和裂隙扩展速度均显著高于S-30。S-30、SN-1和SD-30的起裂应力(微裂纹总数量达到峰值应力时微裂纹总数量1/10时的轴向应力)分别为16.64 MPa、14.11 MPa和12.72 MPa，说明：20°&30°和30°&30°的结构面组合对微裂纹的扩展发育均具有明显的促进作用，使得SN-1和SD-30相对于S-30在较低的轴向应力下发生了颗粒之间联结的张性破坏，形成微裂纹并进一步扩展，最终形成贯穿的宏观破坏面。需要指出的是，SN-1与SD-30在微裂纹起裂阶段有一定的差异，即：SN-1中的微裂纹初始发育、扩展要略慢于SD-30；而，在轴向应力接近0.75σc时，SN-1微裂纹扩展速度增大，之后二者微裂纹数量和扩展速度基本一致，最终破坏时的峰值应力也相近。

图13 最不利结构面的倾角为40°和50°时试样的 微裂纹数量-轴向应力曲线Fig.13 The curves of total cracks number to axial stress for the specimens with same weakest joint of 40° and 50°

最不利结构面的倾角为40°和50°时，单裂隙试样、非等倾角双裂隙和等倾角双裂隙试样在单轴压缩作用下的微裂纹总数量-轴向应力曲线如图13所示。在图13中，当最不利结构面的倾角为40°或50°时，等倾角和非等倾角交叉结构面对试样变形和强度的影响相差不大，试样强度主要受最不利结构面控制。当组合结构面中最不利结构面的倾角在区间②内时，交叉结构面对裂隙试样强度有一定的弱化作用，强度降低较小，且其弱化作用与强度较高的结构面没有明显关联。当最不利结构面相同时，随着两组结构面的倾角差的减小，在裂纹起裂阶段试样中的微裂纹扩展速度增快，即：在相同轴向应力条件下，微裂纹总数量越多。对于沿结构面发生滑移破坏的非等倾角双裂隙试样，其峰值后0.8σc时的张性和剪性破坏分布如图14所示。从图14可以看出，当非等倾角双裂隙试样包含区间②的结构面时，其破坏形式均是沿结构面发生剪切破坏。当两结构面倾角相差较小时，倾角较小的结构面上的平行联结也会有一定程度的破坏，但是并未连接形成贯穿的破坏面；当两结构面的倾角相差较大时，倾角较小结构面上的平行联结几乎没有破坏产生。故可以推断，当非等倾角双裂隙试样的结构面处于区间②内时，其破坏形式仅由倾角较大的结构面控制，与另一倾角较小的结构面无关。

最不利结构面的倾角为40°和50°时试样的起裂应力,如表6所示。从表6中可以看出，在最不利结构面的倾角为40°或50°时，单裂隙试样的起裂应力最高，且当试样中存在两组交叉结构面时，试样的起裂应力有随着另一组强度较高的结构面倾角增大而减小的趋势。

图14 试样S-40、S-50与对应双裂隙试样的峰后破坏分布图Fig.14 Failure mode for model S-40, S-50 and the corresponding double joint models with different dip angles

试样编号S-40SD-40S-50SD-50SN-2SN-3SN-4SN-5SN-6起裂应力/MPa12.910.357.636.1910.877.3210.657.366.86

3 结 论

本文研究了交叉结构面的相互作用及其对岩体试样变形和破坏过程的影响。主要结论如下：

1)对于包含等倾角交叉结构面的双裂隙试样，当倾角在区间①和③时，相比于单条结构面，交叉结构面的相互作用对试样的强度和起裂应力有显著的弱化作用；当倾角在区间②内时，交叉结构面的相互作用对试样的强度和起裂应力也有一定的弱化作用，但其弱化程度较低。

2)对于等倾角双裂隙试样，当倾角小于结构面摩擦角且接近区间③时，其破坏形式为张性破坏，而对应的单裂隙试样的破坏形式为沿结构面破坏；当倾角在区间③时，其破坏形式为沿结构面破坏模式，而对应的单裂隙试样的破坏形式为混合破坏；当结构面倾角显著小于或大于结构面摩擦角时，其破坏形式与单裂隙试样的破坏方式相同。

3)对于包含非等倾角交叉结构面的双裂隙试样，当最不利结构面的倾角在区间①或③时，相比于单条结构面，交叉结构面的相互作用对试样的强度和起裂应力有显著的弱化作用；当最不利结构面的倾角在区间②时，交叉结构面的相互作用对试样的强度和起裂应力影响较小，且其弱化作用随着倾角差的增大而减小，且均小于等倾角双裂隙试样的弱化作用。

4)对于包含非等倾角交叉结构面的双裂隙试样，当最不利结构面的倾角在区间③时，其破坏形式变为沿结构面发生破坏，不同于单裂隙试样的混合破坏模式；当最不利结构面的倾角在区间②时，则其破坏形式仅由倾角较大的结构面控制，均为沿结构面发生剪切破坏。

5)随着轴向荷载增大，结构面交汇处发生应力集中，促进了微裂纹的发展，导致在峰前时相同的轴向应力条件下，双裂隙试样中微裂纹的数量要显著多于仅含最不利结构面的单裂隙试样，即前者的裂纹扩展速度显著大于后者。