癌症疫苗和抑制剂治疗模型整体解的存在唯一性*

刘春燕，卫雪梅，冯兆永，刘成霞

(1. 广东工业大学应用数学学院，广东 广州 510520； 2. 中山大学数学学院，广东 广州 510275； 3. 南方医科大学口腔医院，广东 广州 510280)

当癌细胞发生坏死时，它们释放高活动性组框-1(HMGB-1)激活树突细胞，树突细胞便产生IL-12来激活效应T细胞CD4+Th1和CD8+T。CD4+Th1和CD8+T细胞都能杀死癌细胞[1-3]。CD8+T细胞在杀死癌细胞方面更有效，但CD4+Th1细胞的辅助功能可提高肿瘤反应性CD8+T细胞的功效[4]。癌症疫苗可以扩大肿瘤特异性T细胞的储备，也可以激活休眠的肿瘤特异性T细胞[5]。由于缺乏肿瘤浸润效应T细胞，临床试验中的许多患者对检查点抑制剂治疗没有反应；另一方面，癌症疫苗可以诱导效应T细胞浸润到肿瘤中，而且癌症疫苗和免疫检查点抑制剂的组合可以协同作用以诱导更有效的抗肿瘤免疫回应[6-8]。

早期在文献[9-10]中提出了用常微分方程系统描述癌症疫苗免疫治疗的数学模型，但这些模型没有考虑检查点抑制剂。2017年，Lai等[11]认为疫苗增加T细胞库，检查点抑制剂使T细胞保持完全活性，杀死癌细胞，从而提出了一种将癌症疫苗与检查点抑制剂结合起来的数学模型。在该模型中Lai等进行了数值模拟，对数值解进行渐近分析[11]。具体模型如下：

(1)

(2)

(3)

(4)

(5)

(6)

(7)

0≤r≤R(t),t>0；

(8)

(9)

(10)

(11)

u(0,t)=0；

(12)

D(r,0)=D0(r)；

(13)

T1(r,0) =T1 0(r)；

(14)

T2(r,0) =T2 0(r)；

(15)

C(r,0)=C0(r)；

(16)

G(r,0)=G0(r)；

(17)

I1(r,0) =I1 0(r)；

(18)

I2(r,0) =I2 0(r)；

(19)

P(r,0)=P0(r)；

(20)

A(r,0)=A0(r)；

(21)

R(0)=R0

(22)

h(D,T1,T2,C,G,I1,I2,Q) =

(d1D+d2T1+d3T2+d4C)]

(23)

C+D+T1+T2=N0

(24)

1999年Friedman及其合作者考虑了肿瘤生长的自由边界问题[14]，得到了模型整体解的存在唯一性、稳态解以及解的渐近性态。之后，大量数学工作者对肿瘤生长的自由边界问题进行了一系列研究[15-18]。

根据生物学和医学原理，我们有以下假设：

(A)D0(r),T10(r),T20(r),C0(r),I10(r),I20(r),P0(r),A0(r)∈Dp(0,1)，D0(r),T10(r),T20(r),C0(r),I10(r),I20(r),P0(r),A0(r)≥0。

本文的主要结论如下：

定理1 假设条件(A)满足，则对任意的T>0，系统(1)～(22)的整体解存在且唯一。

1 预备引理

下面我们将介绍一些引理, 首先引入一些记号。

▽u，▽v，Δu，Δv∈Lp(ΩT)}

且规定

0≤z≤1，0≤τ≤T;

(25)

z=0，1：Bc=φ，0≤τ≤T;

(26)

c(z，0)=c0(z)，0≤z≤1

(27)

2 模型的等价形式

考虑到直接解决自由边界问题(1)～(22)的困难性，我们将该自由边界问题变换为固定区域{(z,τ),0≤z≤1,τ≥0}上的初边值问题，以利于讨论其解的适定性。

D′(z,τ)=D(r,t)，C′(z,τ)=C(r,t)，

(28)

P′(z,τ)=P(r,t)，A′(z,τ)=A(r,t)，

u′(z,τ)=R(t)u(r,t)，

Q′(z,τ)=Q(r,t)

(29)

(30)

(31)

(32)

(33)

(34)

(35)

(36)

(37)

(38)

(39)

(40)

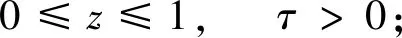
(41)

(42)

(43)

(44)

v(z,τ)=u′(z,τ)-zu′(1,τ),

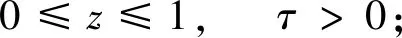
(45)

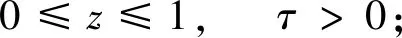
(46)

(47)

u′(0,τ)=0；

(48)

η(0)=R0

(49)

根据以上变换过程，可以得出如下结论：

引理2 在变量替换(28)下，自由边界问题(1)～(22)与初边值问题(29)～(49)等价。

3 局部解的存在唯一性

这部分将证明系统(29)～(49)有唯一的整体解。先通过运用Banach不动点定理证明系统(29)～(49)有唯一的局部解。记

定义空间XT上的度量为

d((U1,η1),(U2,η2))=

显然(XT,d)是一个完备度量空间。由式(46)、式(48)得

(50)

(51)

(52)

(53)

(54)

(55)

(56)

(57)

(58)

(59)

(60)

(61)

(62)

(63)

(64)

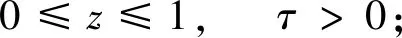
(65)

(66)

(67)

(68)

首先证F是映射空间XT到自身的映射。

(69)

考虑问题(51)，利用条件(i)和(iii)，可得

(70)

结合式(69)得

(I2) 考虑问题(53)～(54)，

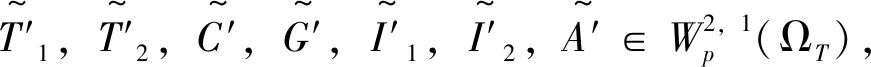
由于

2)

综上所述，若取K>0，则当T>0充分小时，C(T)是有界的，C(T)K≤M，有

利用嵌入定理

得

其次要证当T充分小时，映射F压缩。

(II1) 显然，通过计算可得

因此由式(69)可得

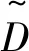
其中

TC(T)Md

(II3) 同理，记

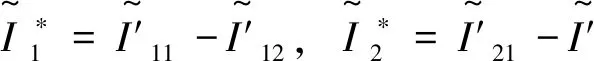
则有

则由情形(II2)～(II4)可得

结合情形(II1)～(II4)，可推出

因此，当T足够小时满足C(T)M<1，此时F为压缩映射。

由上述分析可得如下结果：

定理2 若条件(A)满足，当0≤t≤T时，系统(1)～(22)存在唯一解。

4 整体解的存在唯一性

由上下解原理得

引理3 问题(1)～(25)的解有如下结论

D,T1,T2,C,G,I1,I2,P,A≥0

将式(10)变换为

对上式关于r积分可得

则

将上式代入式(11)得

因此

由此可得

即

(71)

引理4 对任意的1

证明显然，v(z,τ)为连续函数， |h′|≤B为有界连续函数，则由式(45)、式(50)与式(71)可得

且

因此u′(z,τ)与v(z,τ)均为有界连续函数。

同理有

由

可得

(c) 考虑问题(35)～(40)和(43)～(44)，因为

而且显然

(t)均有界且连续，因此同理可得

则有

由情形(a)～(c)可得

继而由

得

由系统(29)～(49)与(1)～(22)的等价性得知

因此引理4得证。根据定理2、引理3和引理4以及时间T的任意性可证得本文的主要结论定理1。