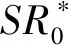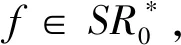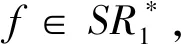伯努利双纽线右半有界区域内广义解析函数类的三阶Hankel行列式*

汤获，张海燕，牛潇萌

(赤峰学院数学与统计学院， 内蒙古 赤峰 024000)

设C表示复平面，A表示在单位圆盘D={z:|z|<1}内解析且适合如下形式

(1)

的函数类。

设函数f(z),g(z)在单位圆盘D内解析，如果存在D内的Schwarz函数ω(z)，满足ω(0)=0，|ω(z)|<1，使得f(z)=g(ω(z))，则称f(z)从属于g(z)，记为f(z)g(z)(见文[1-2])。

用P表示在单位圆盘D内具有如下形式

p(z)=1+p1z+p2z2+

(2)

且满足条件Re(p(z))>0的解析函数族。若p(z)∈P，则|pn|≤2(n=1,2,)(见文献[2])。

1996年，Sokol 和 Stankiewicz在文[3]中引入了伯努利双纽线右半有界区域内的解析函数类SR*，并讨论了该类函数的凸半径问题。

定义1 设SR*表示定义如下

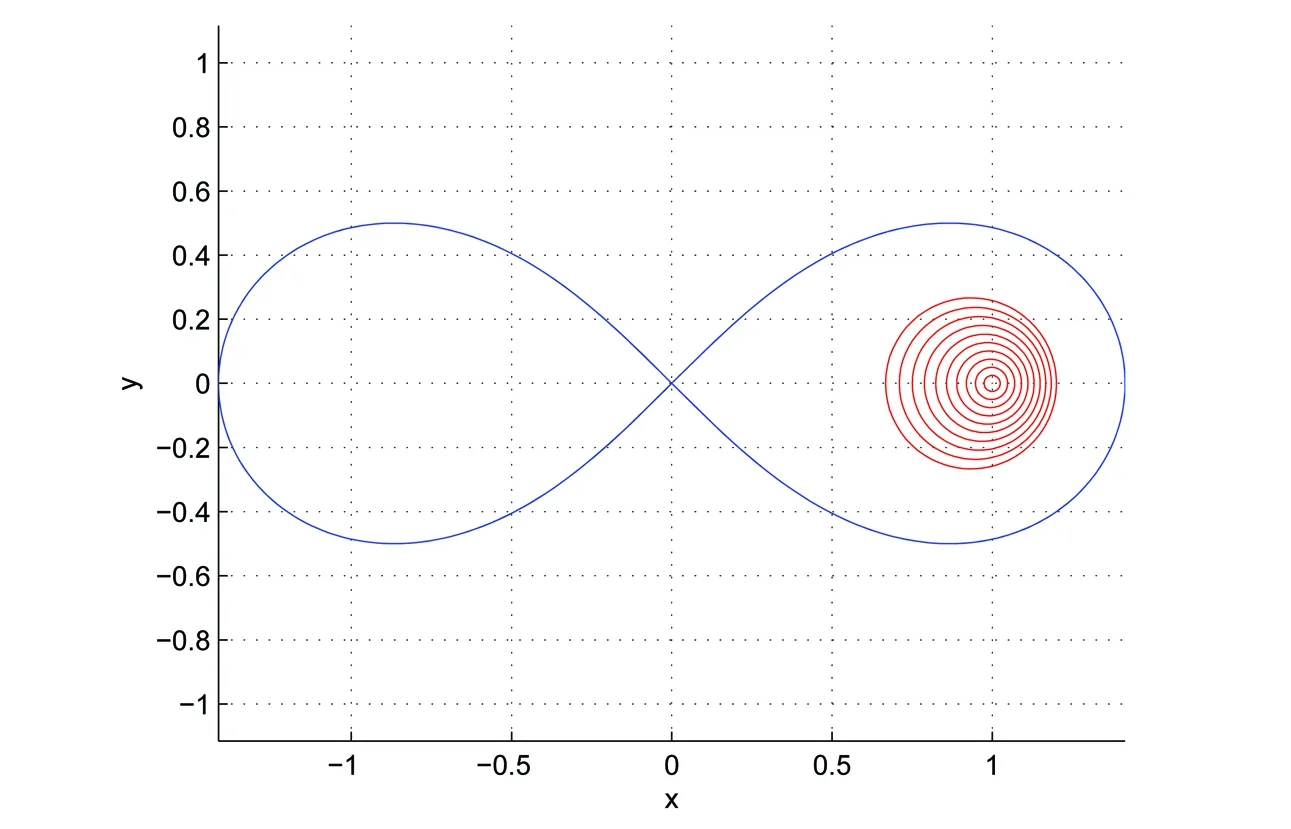
图1 函数类SR*的图像(其中Fig.1 The graph of the function classSR*

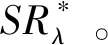
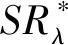
(3)

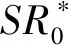
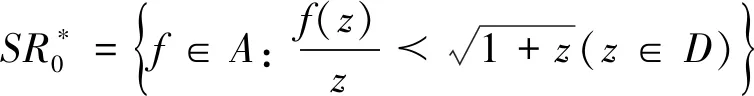
{ω∈C:Reω>0,|ω2-1|<1}的伯努利双纽线右半有界区域内(见图2)。

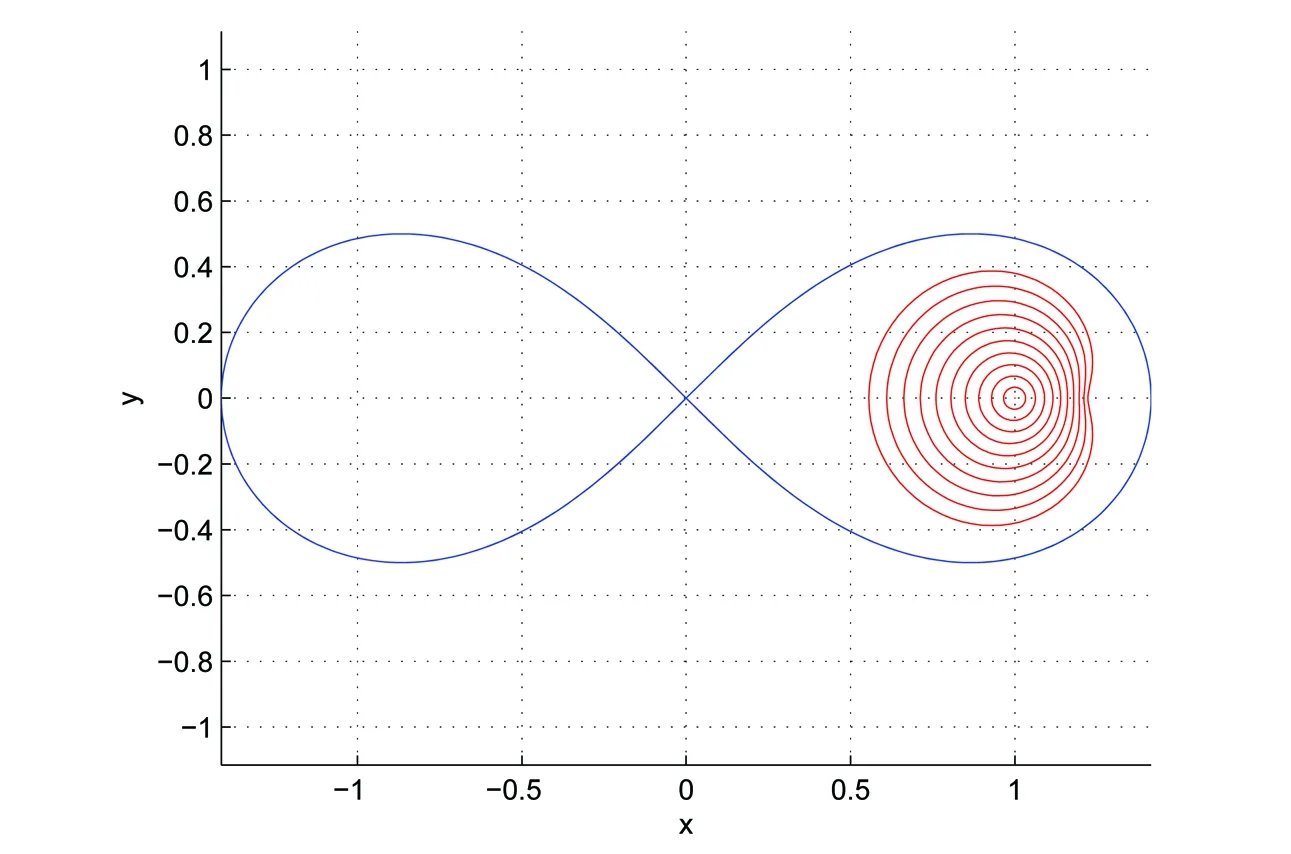
图2 函数类的图像

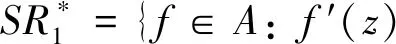
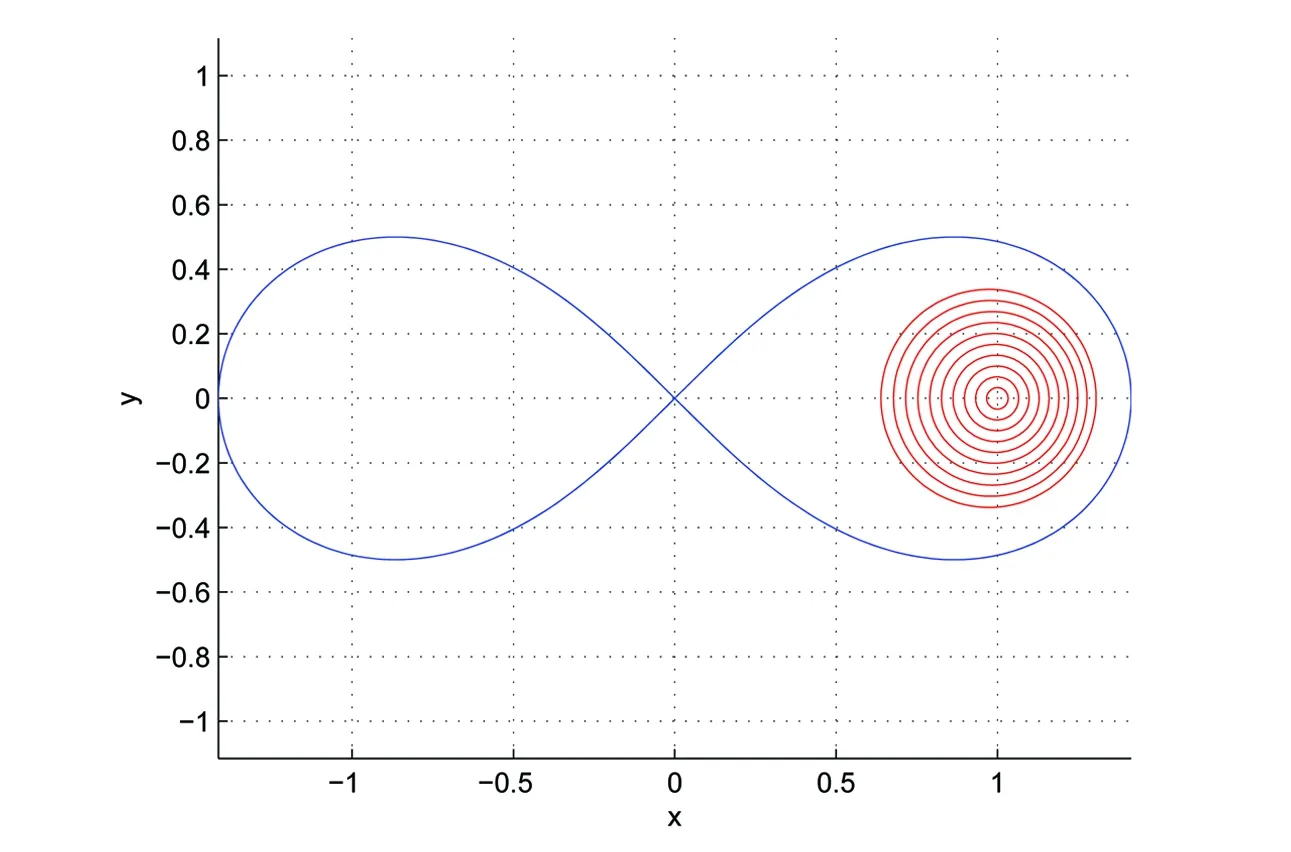
图3 函数类的图像

1976年，Noonan和Thomas 在文[4]中引进函数f的q阶Hankel行列式Hq(n)，其定义如下：

其中n≥1，q≥1。

特别地，若f∈A,a1=1，则有

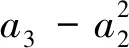
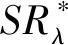
1 若干引理

为了证明本文主要结论，我们需要如下引理。

引理1[17]如果p(z)∈P适合式(2)，则有

(4)

且

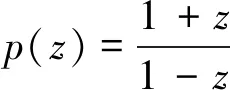
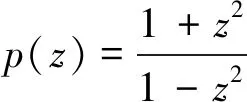
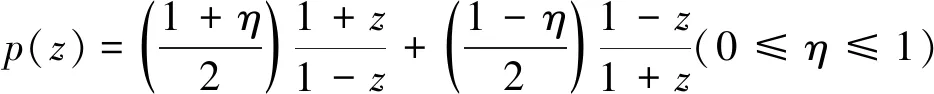
(iv)如果υ=1，则当且仅当p(z)是使得υ=0时等号成立的函数的倒数。

引理2[17]如果p(z)∈P适合式(2)，则对于任一复数υ，有

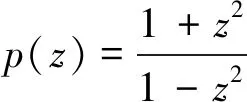
引理3[18]如果p(z)∈P适合式(2)，则存在复数x,z满足|x|≤1,|z|≤1,使得

2 主要结果及其证明

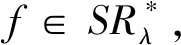
且

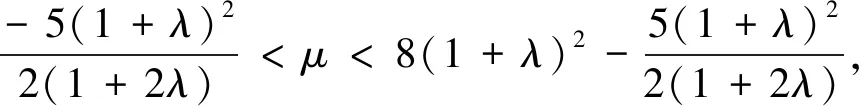
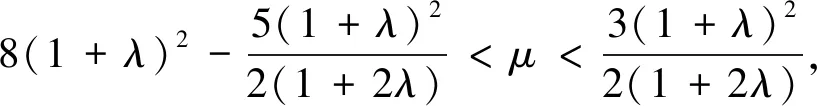
并且这些结果都是精确的。

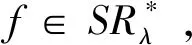
(5)

利用式(5)和从属关系，有

(6)

定义函数

显然，p(z)∈P，这意味着

(7)

综合式(6)和式(7)，可得

而

1+(1+λ)a2z+(1+2λ)a3z2+

(1+3λ)a4z3+

分别比较上两式中z,z2和z3的系数，并经简单计算可得

机组电源由于发电机输出受电机磁通限制等一系列因素制约，输出频域不可能太广。而对于电力电子变频器为核心的静态变频电源而言，可以轻松实现宽频域输出。例如，本厂重型试验站和18 000 kW试验站均实现了1～120 Hz输出或者12～80 Hz正弦满容输出，而风电试验站和直流试验站的机组电源设计上均只能满足45～65 Hz满容输出。

(8)

(9)

(10)

进一步，根据式(6)和式(7)，有

再用引理1，可得

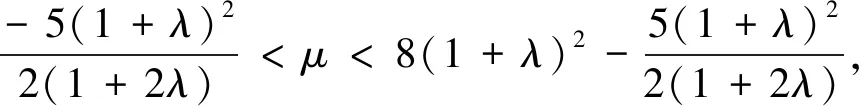
定理1证毕。

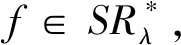
证明由于

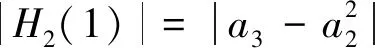
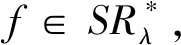
(11)

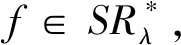
(12)

证明由式(8)-式(10)，有

设p1=c∈[0,2]，|x|=t∈[0,1]，则由三角不等式及引理3，可得

|32c(1 + 2λ)2(4-c2)(1-t2) + 8λ2(4-c2)c2t+

16(4 + 16λ+ 12λ2+λ2c2)(4-c2)c2t2+

(1 + 4λ+ 5λ2)c4|

记

[32c(1+2λ)2(4-c2)(1-t2)+

8λ2(4-c2)c2t+16(4+16λ+12λ2+λ2c2)

(4-c2)c2t2+(1+4λ+5λ2)c4]

假设F(c,t)在矩形区域[0,2]×[0,1]的内部点存在上界，将上式关于t求导，有

[32(4+16λ+12λ2+λ2c2)(4-c2)c2t-

64c(1+2λ)2(4-c2)t]

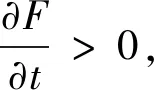
maxF(c,t)=F(c,1)=

[8λ2(4-c2)c2+16(4+16λ+12λ2+λ2c2)·

(4-c2)c2+(1+4λ+5λ2)c4]

令

[8λ2(4-c2)c2+16(4+16λ+12λ2+λ2c2)·

(4-c2)c2+(1+4λ+5λ2)c4]

则

[190λ2c-96λ2c3-32(4+16λ+12λ2+λ2)c+

4(1+4λ+5λ2)c3]

[190λ2-288λ2c2-32(4+16λ+12λ2+λ2)+

12(1+4λ+5λ2)c2]

因为c=0是G′(c)=0的根，且G′′(c)<0，所以函数G(c)在c=0处取得最大值。 综上可知，函数F(c,t)在t=1，c=0处取得最大值，即有

定理3得证。

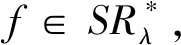
(13)

证明由式(8)-式(10)，有

设p1=c∈[0,2]，|x|=t∈[0,1]，则由三角不等式及引理3，可得

|16(1+λ)(1+2λ)(4-c2)(1-t2)+

(8+24λ+8λ2)(4-c2)ct+8(1+λ)(1+2λ)·

(4-c2)ct2+(2+6λ+2λ2)c3|

记

[16(1+λ)(1+2λ)(4-c2)(1-t2)+

(8+24λ+8λ2)(4-c2)ct+8(1+λ)·

(1+2λ)(4-c2)ct2+(2+6λ+2λ2)c3]

假设F1(c,t)在矩形区域[0,2]×[0,1]的内部点存在上界，将上式关于t求导，有

[(8+24λ+8λ2)(4-c2)c+

16(1+λ)(1+2λ)(4-c2)ct-

32(1+λ)(1+2λ)(4-c2)t]

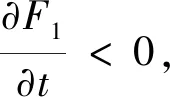
maxF1(c,t)=F1(c,0)=

令

G1(c)=

则

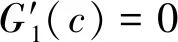
定理4得证。

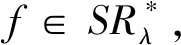
(14)

(15)

(16)

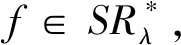
[(1-λ)f(z)+λzf′(z)]2=z2(1+ω(z))

其中ω(z)是Schwarz函数且满足

ω(0)=1,|ω(z)|<1,z∈D

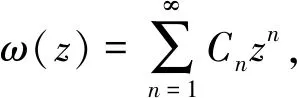
[(1-λ)f(z)+λzf′(z)]2=

[z+(1+λ)a2z2+(1+2λ)a3z3+

(1+3λ)a4z4+]2

所以有

[z+(1+λ)a2z2+(1+2λ)a3z3+

分别比较上式中z3,z4,z5,z6的系数，并经简单计算可得

又因为|ω(z)|<1，|z|≤1，|Cn|≤1，故

定理5得证。

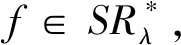
|H3(1)|≤

证明由于

故由三角不等式，可得

(17)

将式(11)～(16)代入式(17)，即得定理6。