基于广义Pareto分布的洪水序列频率分析*

赵玲玲，陈子燊，刘昌明，许扬生

(1. 广州地理研究所广东省地理空间信息技术与应用公共实验室，广东 广州510070； 2. 中国科学院地理科学与资源研究所中国科学院陆地水循环及 地表过程重点实验室，北京100101； 3. 中山大学地理科学与规划学院，广东 广州510275； 4. 北京师范大学水科学研究院，北京1008755； 5.广东省水文局，广东 广州 510050)

变化环境下导致极端事件呈现增加趋势，其中洪水属于典型的灾害事件。基于有限的水文观测数据中发现尽可能多的洪水的规律，提高推算洪水重现水平的精度，对防洪工程规划设计和灾害风险评估有重要作用。超限频率分析是极值统计建模理论的重要组成部分[1]，国内外已有不少探索与研究。研究人员对超定量样本的频率分布线型的适用性做了较多研究，如指数分布[2-3]、Gamma分布和Weibull分布[4]。之后研究集中在广义Pareto分布(GPD)[5-8]。而GPD应用于实际数据集的成功与否很大程度上取决于参数估计过程。Hosking等[9]使用极大似然法(ML)和概率权重矩法(PWM)估计GPD模型的参数，Zhang[10]提出了基于GPD的参数估计似然矩法。Bermudez等[11-12]详细介绍了多数情况下使用的最大似然(ML)、概率加权矩(PWM)和矩法(MOM)参数估计方法及其优缺点。王剑峰等[13]用常规线性矩法和改进线性矩法对广义Pareto分布参数进行估计，并对比分析了超定量序列频率。周长让等[14]采用高阶概率权重矩估计其分布参数，统计试验表明该方法具更高的参数估计精度，估参结果对应的GPD曲线能较好地拟合稀遇频率洪水段的经验频率分布。但在洪水超限频率分析中如何选取阈值这一关键问题、超定量数和超定量分布的拟合优度检验等还需要更多的探索与实践[7]。

本文以山区中小流域日流量过程为例，深入探讨广义Pareto分布(GPD)模型的阈值选择方法，洪水序列超定量数检验、拟合优度检验，最后对GPD、GEV分布与P-III型分布推算的设计水平加以对比。

1 极值分布模型

单变量极值分布模型有2种常用方法：一是分组区块最大值模型(block maximum group of models，BM)。首先是对所得到的数据进行分块，常用年最大值方法(annual maximal series，AMS)采用年最大值样本作为建立模型的观测值。BM模型的要求数据样本独立同分布(IID)。而对洪水序列而言，常常一年内出现多次洪水样本，所以按年最大值抽样后会出现多个洪峰流量远大于枯水年份出现的最大值的现象。按年最大值抽样显然会造成洪水信息利用不充分；二为峰量超阈值模型(peaks over threshold models，POT)，其选取超特定阈值抽取样本，该方法可获取较多的洪水极值序列建立模型。POT模型要求满足超定量发生的时间服从泊松分布，且彼此相互独立服从GPD(generalized Pareto distribution)分布)[8]。

1.1 广义Pareto分布

设序列{xn} 的分布函数为F(x)，定义Fμ(y)为随机变量X超过阈值μ的条件分布函数：

Fμ(y)=

P(X-μ≤x|X>μ)=

⟹F(x)=Fμ(y)(1-F(μ))+F(μ)

(1)

研究表明[18-20]，当μ阈值足够大时，条件超量分布函数Fμ(y) 收敛于广义Pareto分布，累积分布函数为：

Fμ(y)≈G(x,ξ,σ,μ)=

(2)

式中，ξ、σ、μ分别为形态参数、尺度参数和位置参数。当ξ=0时，GPD对应于指数分布,为Pareto I型分布；当ξ<0时为Pareto II型分布，x∈[μ,∞)；当ξ>0，为Pareto III型分布(短尾型)。有关研究证明了超定量(X-μ)数服从泊松分布[17]。

GPD模型T年一遇的分位数xT为：

(3)

1.2 超定量洪水序列阈值确定

阈值μ的合理确定是GPD模型参数ξ和σ正确估计的前提。μ取值过高，超限数据量少，使估计出来的参数方差很大；相反μ取值过低，则难以保证分布的收敛性，估计偏差较大。阈值选取基本原则：对于每次洪水过程，选取洪峰流量最大值；不同场次洪峰取样时，各场次洪峰发生时间间隔要求大于流域的汇流时间，以保证不同洪水之间相互独立。采用以下4种相结合的方法确定μ：

1)绘制样本的经验平均超过函数图

令X(1)>X(2)>>X(n)，样本的经验平均超过函数定义为[21]：

(4)

其中

k=min{i|Xi>μ}

绘制的平均超过函数图即为点(μ,e(μ))构成的曲线，选取较大的μ作为阈值，它使得当x≥μ时e(x)为近似线性函数。当x≥μ时平均超过函数图曲线向上倾斜，表明点据服从形状参数ξ为负的GPD分布，属于II型分布。当x≥μ时曲线向下倾斜，表明数据源自于尾部较短的分布，当x≥μ时曲线是水平的，表明该数据服从指数分布。因此，如果某个阈值μ后的e(n)趋向于新的线性变化时，可选取这个值为阈值。

2)Anderson-Darling(AD)检验

AD检验属于平方根类经验分布函数统计检验，采用AD检验GPD模型的超定量样本的经验分布和理论分布的拟合优度时，AD检验在小频率的上尾部区域赋予了更多权重。

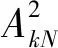
(5)

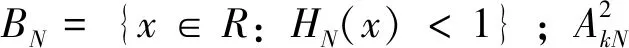
3)泊松分布检验

为了保证所选样本的独立性，选择一定的阈值区间，在显著水平0.05下，分别对阈值区间内不同阈值的超限数采用χ2假设检验其是否服从泊松分布：

P(x=k)=e-λλk/k！，k=0，1，2，

其中λ为平均发生超限的频次。对服从泊松分布样本的阈值再根据其它拟合优度检验指标作进一步的筛选。

4)初始阈值与洪水序列的确定

以枯水年最大洪峰流量值为初始阈值，根据流域汇流时间形成阈值区间，采用不同的汇流时间间隔分别抽取不同间隔时段内不同序列的洪峰阈值，在显著水平0.05下，对各超定量样本数的做独立性检验。对确定的洪水序列样本估计分布参数值及其拟合优度检验值。

通过以上4种相结合的方法对于确定最终采用的超阈值洪水序列样本满足独立性，阈值μ为优选值。

2 实例研究

2.1 研究背景与基本数据

选取广东强降水地区典型中小流域-曹江流域作为研究对象。曹江是粤西独流入海鉴江的一级支流，发源于高州马贵镇山心村海拔1 141 m的蓝蓬岭，中上游雨量充沛，是广东的暴雨高区之一，流域坡降大汇流时间短，洪水陡涨陡落，导致洪灾频发，对当地造成严重的生命威胁与经济损失。流域多年平均年雨量2 160 mm，最大平均年雨量为3 150 mm。曹江流域出口断面大拜水文站集水面积394 km2。

利用1967～2013年共47年大拜站逐日流量观测序列分析曹江流域洪水的超阈值频率分布特征。流量序列日最大值778 m3/s，最小值仅0.46 m3/s，日平均流量19.4 m3/s。对大拜站流量序列的洪水过程统计表明，通过大拜站的洪水平均传播时间绝大多数为1～3 d，最长历时可达10 d(2010年9月21～30日)。

2.2 洪水阈值

采用以下步骤确定曹江流域洪峰流量阈值：

1)在平均超过函数图(图1)内流量序列在100 m3/s左右存在线性变化折点，随之曲线向上倾斜，表明点据服从形状参数为负的GPD分布，可考虑选取线性变化折点值为参考阈值。

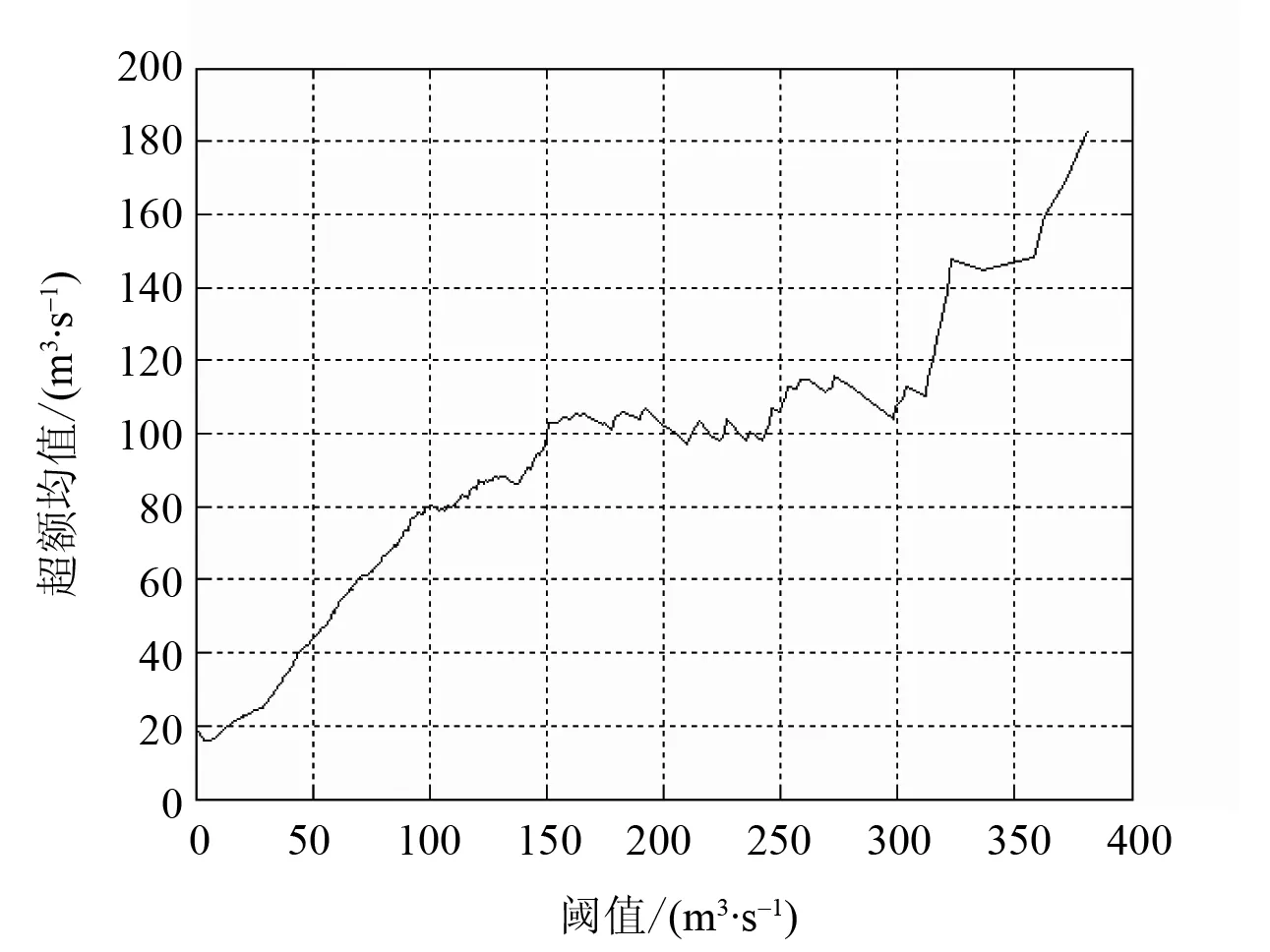
图1 超限样本的经验平均超过函数图Fig.1 Definite mean excess function chart

2)以枯水年(2007年)最大洪峰流量值74 m3/s为初始阈值μ0，形成阈值区间：μi=μ0+(i-1)×10，i=1,,15，阈值选择范围为74～214 m3/s。

3)按不同洪水序列之间相互独立的要求，根据流域汇流时间短的特点，以3 d时间为初始间隔时段，以1 d为步长增量逐步增加至10 d时间间隔，按照步骤1)分别抽取不同间隔时段内不同序列的洪峰阈值，在显著水平0.05下，对各超定量样本数的泊松分布加以χ2检验(表1中原假设，H0=0：样本服从泊松分布)；为节省版面，文中仅列出采用参数概率权重矩估计和极大似然估计法4，6，8和10 d时间间隔的洪水序列样本的参数估计值及其拟合优度检验值。

4)超限抽样系列的AD检验的P值都远大于α=0.05的临界值，超定量样本的频率分布与理论CDF拟合良好，表明该超限样本符合GPD分布。除去不符合泊松分布的超限样本和λ<1的超限样本后发现，在8种采样时间间隔的洪峰序列中阈值为104 m3/s的超限样本的PAD值最大，其中采样时间间隔中间隔8 d的PAD值和PPCC(概率图位相关系数)值最大，RMSE(均方根误差)最小。因此104 m3/s可作为大拜站洪水序列的日洪峰流量序列的优选阈值(表1)。

2.3 GPD参数估计与拟合优度检验结果

极值分布模型的参数估计是统计分析的关键点之一。不同的参数估计方法推算的分布参数直接影响极值重现水平。因此本文使用具有统计特性良好的概率权重矩法(PWM)和极大似然法(ML)[6]估计模型的参数，对各超限样本的GPD重现水平的推算结果进一步采用了PPCC和RMSE作为拟合优度检验指标，主要结果如下：

1)PPCC值均大于0.984，表明各个超定量样本点据与理论分布值的相关关系达0.984以上。同时PWM参数估计方法得到的GPD模型的均方误差RMSE小于ML拟合的模型误差，其中λ=2.0-3.0估计的指标更可靠，拟合优度检验结果见表1。

2)模型的形态参数为负值，表明曹江洪水序列服从Pareto II型分布。

前述结果显示，GPD模型确定超定量洪水是根据多个指标综合分析确定的动态过程。

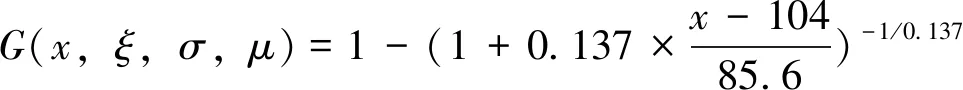
2.4 不同概率分布模型对比分析

对比GPD和GEV两种极值分布及P-III型分布推算参数的分布函数拟合指标值，P-III型分布参数估计使用常规矩法(OME)和线性矩法(L-M)。三种模型最优模型参数和拟合优度检验指标见表2，各分布模型推算的洪水重现水平见表3和图2～4。

三种概率分布的拟合优度指标对比显示，超限量抽样在满足超限量数服从泊松分布，超限彼此相互独立条件下构建的GPD模型，在介于2.0～3.0之间构建的GPD模型精度优于GEV和P-III型，图2显示，大拜站超定量洪水频率曲线图上的样本点与理论曲线非常吻合，尤以PWM参数估计推算的GPD模型最佳。以8 d为抽样间隔的拟合优度检验指标为例，阈值74～124 m3/s范围内，采用PWM参数估计方法拟合的GPD模型PPCC值大于等于0.984，以阈值104 m3/s对应的PAD和PPCC值最大，RMSE也明显小于P-III分布和GEV分布。

同频率设计值对比结果表明，设计频率小于2%(重现期50年)时，GPD模型设计值介于GEV和P-III之间，随着设计频率增大，GPD设计值超过GEV和P-III分布的设计值(表3)。此或反映了自然流域洪水过程的差异性，其原因需要通过更多的实证加以归纳说明。

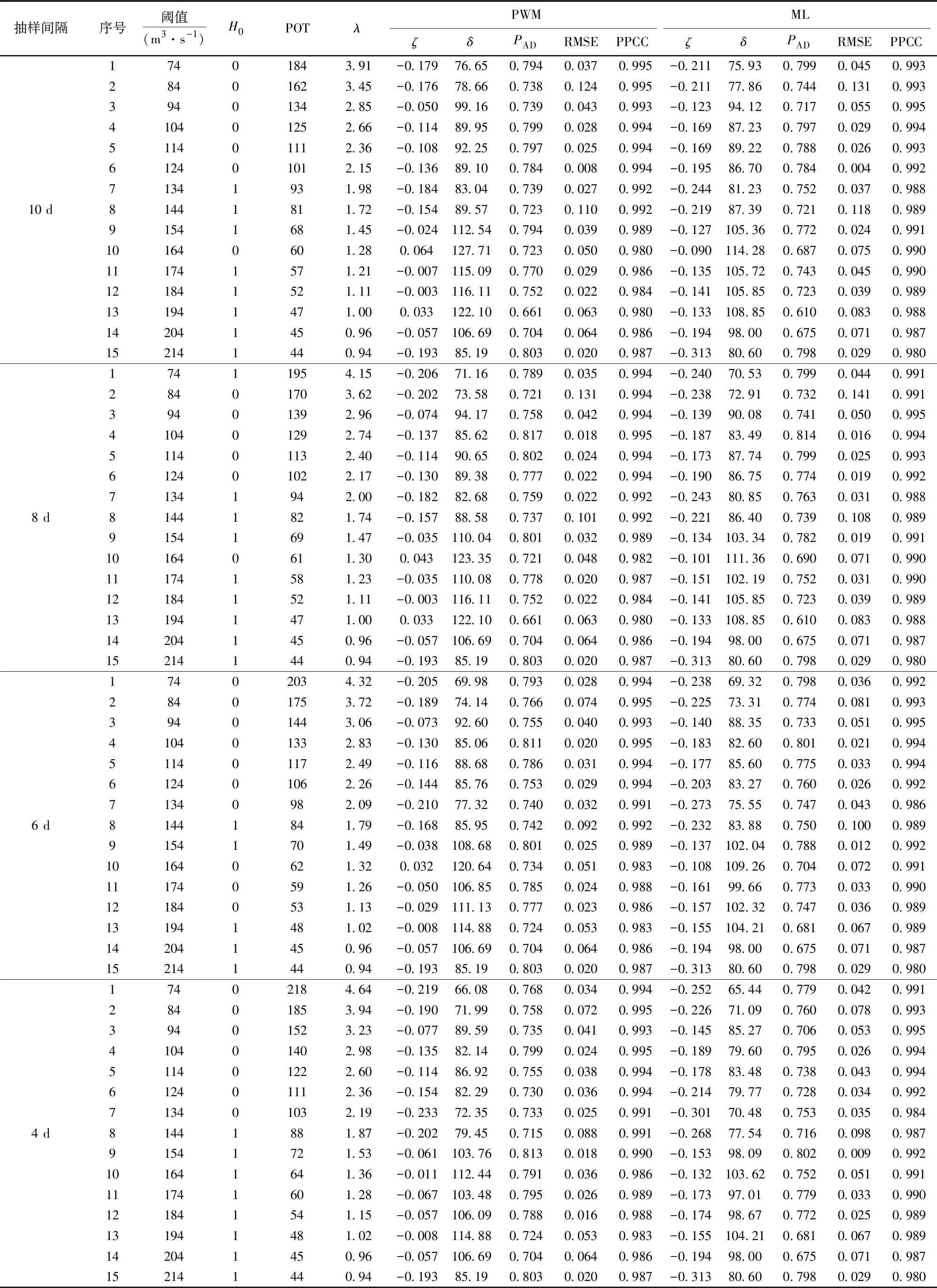
表1 GPD模型的阈值、参数估计与拟合优度检验结果Table 1 The selected threshold values, estimated parameters and goodness-fit test of GPD models

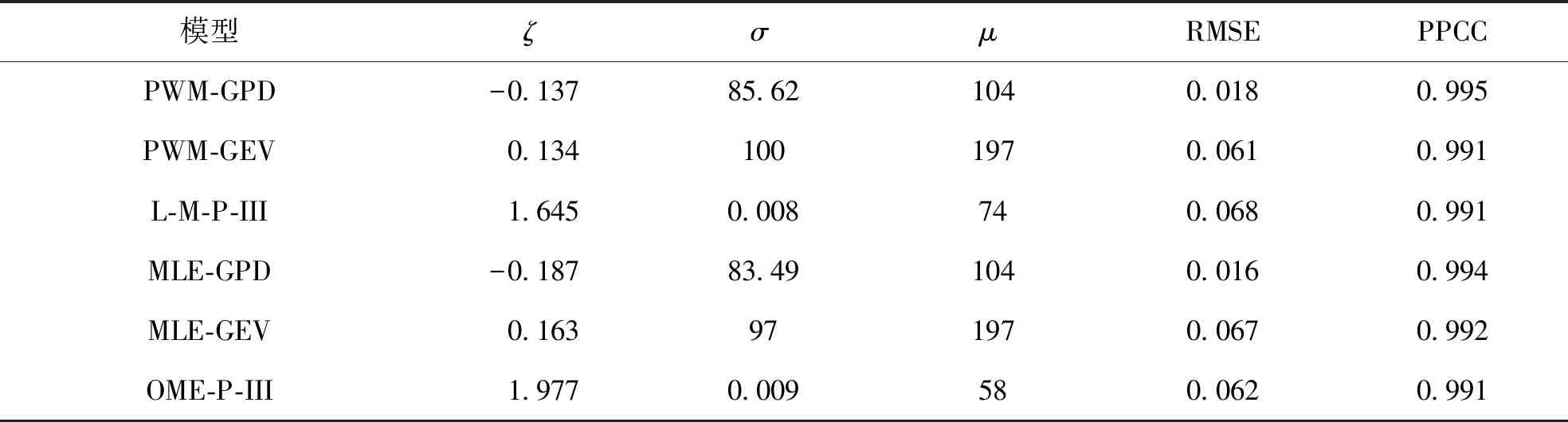
表2 最优GPD、GEV、P-III分布参数与拟合优度检验对比Table 2 Comparison of parameters and indicators of goodness-fit test among the optimal GPD, GEV and Pearson Type III models

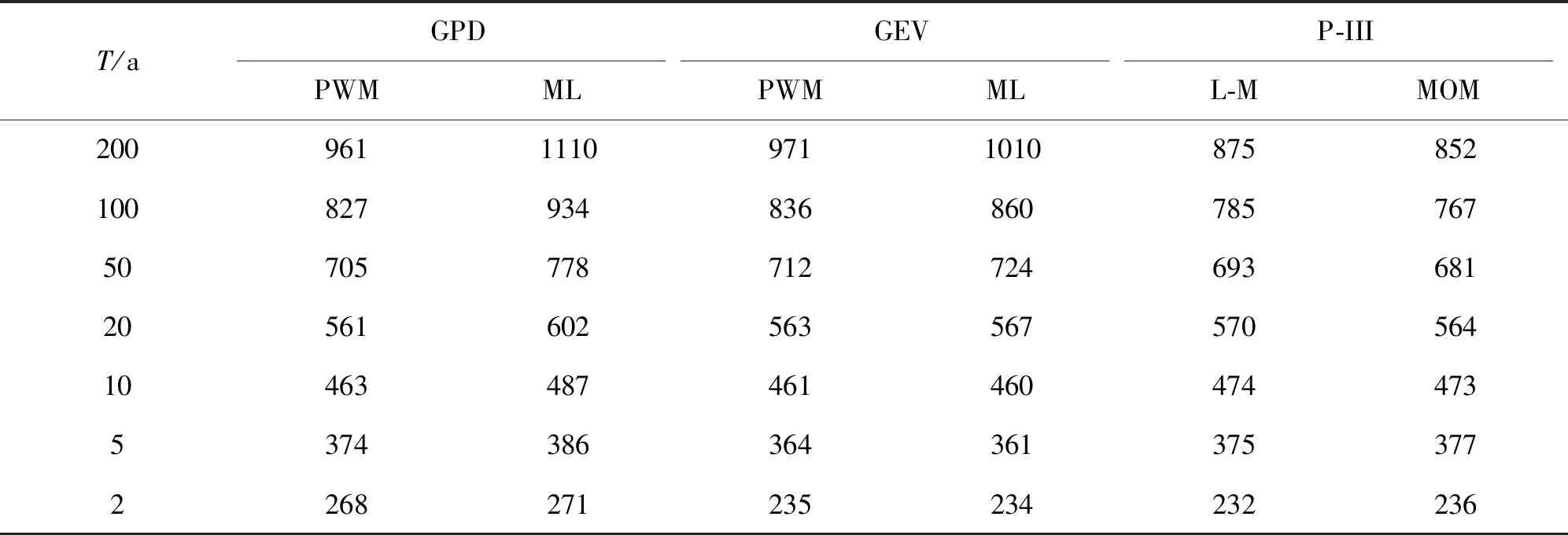
表3 三种概率分布函数洪水重现水平值Table 3 Return levels of flood discharge of three probability distributions m3/s

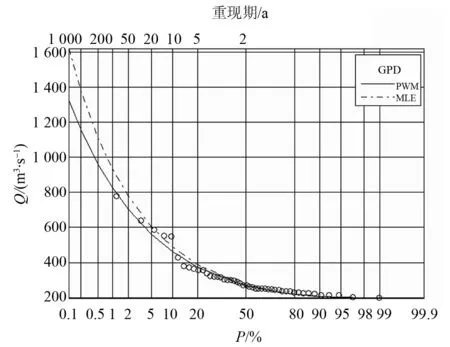
图2 大拜站超定量洪水频率曲线图Fig.2 POT flood frequency curvesforDabaistation

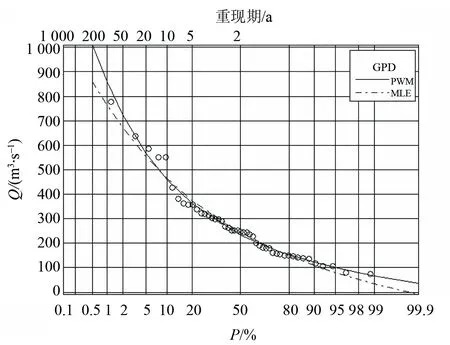
图3 大拜站年最大洪水GEV分布频率曲线Fig.3 Annual maximal flood frequency curves basedGEV distribution forDabaistation

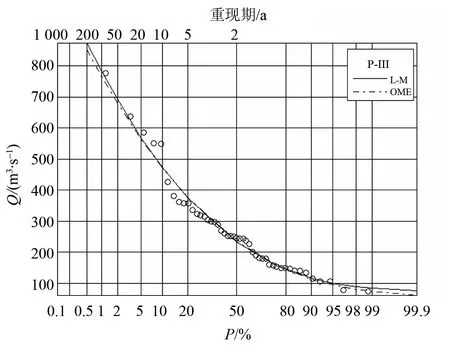
图4 大拜站年最大洪水P-Ⅲ分布频率曲线Fig.4 Annual maximal flood frequency curves based Pearson Type III distribution for Dabai station

3 结 论

1)GPD模型的形态参数表明洪水频率分布属于II型，与短尾分布III型不同，II型表明密度分布函数峰值右侧分布曲线与横坐标之间的渐进性而无切点，难于确定洪水的上限值。此是否反映了山地流域不同时段不同区域土壤含水量差异大和洪水的产汇流过程不确定性的自然属性，有待更多的实例研究。

2)确定超定量洪水GPD 模型是动态择优过程，对多个满足GPD模型要求的阈值，需要通过超定量数的泊松分布检验和超限样本的拟合优度等综合评判后构建相对最优GPD模型。

3)GPD模型推算的设计洪水精度普遍优于GEV分布和P-III型分布的推算成果。

4)不同参数估计方法对于极值模型参数推算精度有较大影响。POT样本由PWM法估计参数的极值模型精度高于ML法推算的结果。