基于递归性质的伪梅森素数的生成方法*

张艳硕 周岐浩 刘 冰 滕树晨

北京电子科技学院，北京市 100070

1 引言

梅森素数[1]是数论研究中的一项重要内容，自古希腊时代起人们就开始了对梅森素数的探索。由于这种素数具有独特的性质，一直吸引着欧几里得、费尔马、欧拉等众多数学家和无数的数学爱好者对它进行探究。在现代，梅森素数在计算机科学、密码学等领域也有重要的应用价值。20世纪90年代中后期，建立了世界上第一个基于互联网的分布式计算项目——因特网梅森素数大搜索[3](GIMPS)。2017年12月26日发现了第50个梅森素数，超大素数有23249425位数，再次刷新了已知最大素数纪录。

伪梅森数是最近提出的根据梅森数变形的具有(2P-c)形式的一类数，其中p为素数，c为小奇数，并用M(p，c)表示。当c＝1时，伪梅森数即为梅森数。另外，当一个数既是伪梅森数又是素数时，将其称为伪梅森素数[7]。

伪梅森数的提出大大地拓宽了大素数的产生渠道。发现伪梅森素数需要素数判别和数值计算的理论与方法以及高超巧妙的程序设计技术。它促进了分布式计算技术的发展，在推动计算机功能改进方面发挥了独特作用。伪梅森素数的研究推动了数论的发展，促进了计算数学和程序设计技术的发展[5]。

本文根据伪梅森数的定义推出一些相关性质并提出基于递归性质的伪梅森数的生成方法以及伪梅森数在构造RSA[6]密钥、ElGamal[2]密钥和Diffie-Hellman[4]密钥协商上的应用。

2 伪梅森数

本文先从梅森数的定义[1]列出有关伪梅森数的两个定义。

定义1将形如2p-c形式的正整数用M(p，c) 表示，其中p为素数，c为3、5、7 等小奇数，称为伪梅森数。当M(p，c)为素数时，我们将其称为伪梅森素数

如：M(3，3)＝ 5 为伪梅森素数，而M(5，5)＝27为伪梅森数而非伪梅森素数。

注：针对定义1特殊说明整数2为唯一的偶素数，表示为M(2，2)，这个是c唯一为偶数的情况。本文对M(2，2)作为特殊情况另行讨论。当c＝1时，伪梅森数退化为梅森数。

定义2约束定义：若整数 k同时满足M(p1，c1)和M(p2，c2)，且p1＜p2，即

那么将k定义为伪梅森数M(p1，c1)而非M(p2，c2)。

如：3＝M(2，1)＝M(3，5)，根据定义2，将3定义为M(2，1) 而非M(3，5)。

这里规定了整数k的最简定义，避免了重复定义造成的资源浪费。

3 伪梅森素数的性质

本文从伪梅森数与梅森数关系以及伪梅森数之间的递归关系，推出了伪梅森数的7个性质。

性质1对于任意素数p，奇数c1，c2，c3有

证明：

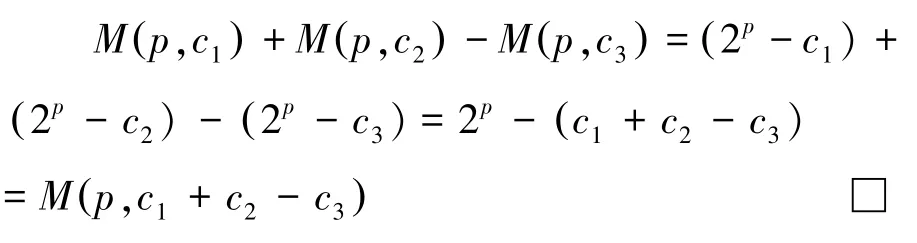
性质2对于任意素数p，奇数 c，有M(p，c)与c互素。

证明：

性质3对于任意素数p，奇数c，若满足2N-1＜c＜2N，则对于伪梅森数M(p，c)有：

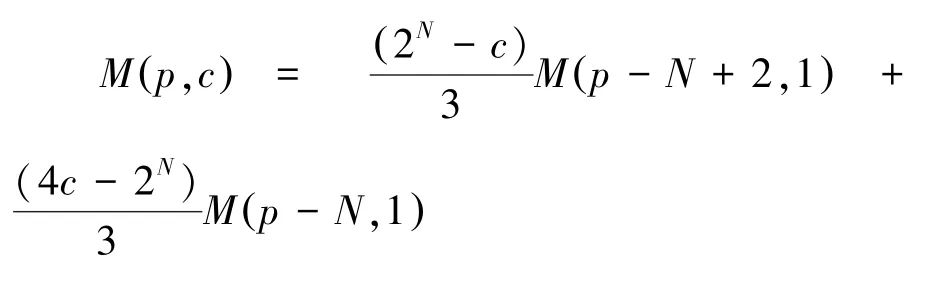
证明：

假设

利用该定理可以利用两个小梅森数构造大的伪梅森数。

推论1：当N是偶数且c≡1mod6时，和均为整数，或当 N是奇数且 c≡5mod6、时，均为整数。

证明：

①若N是偶数，则2N-1≡0mod3

伪梅森数的定义中c为奇数，则

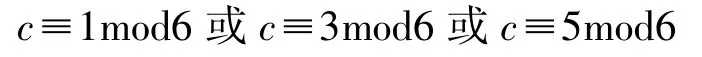
所以：

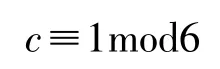
②若N是奇数，则2N-1≡1mod3。

伪梅森数的定义中c为奇数，则

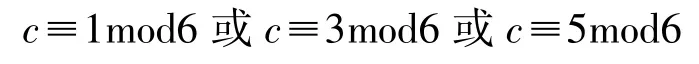
所以：

性质4对于任意素数p1，p2，小奇数c1，且p1≥p2，有

性质 5对于任意素数p1，p2，奇数c1，c2，且p1≥p2，有

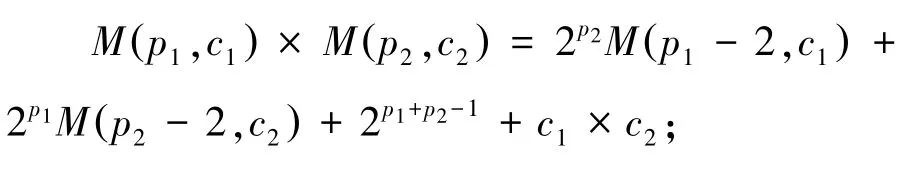
证明：

性质6对于任意素数p1，p2，小奇数c1，c2，且p1≥p2，有

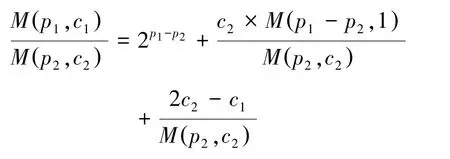
证明：

特别的，当c1＝c2＝c时，上式变为

注：根据上述等式判断M(p1，c)与伪梅森素数M(p2，c)的互素情况，当等式右边为非1整数时，M(p1，c)与M(p2，c)不互素，否则二者互素。由于2p1-p2为整数，只需判断的整数性。

由性质2可知M(p2，c)与c互素，故当2M(p1-p2-1，1)＋1与M(p2，c)互素时M(p1，c)与M(p2，c) 互素。由此我们得到性质7：

性质7对于任意素数p1，p2，小奇数c，且p1≥p2，M(p1，c)与伪梅森素数M(p2，c) 互素的充分必要条件为 2M(p1-p2-1，1)＋1与M(p2，c) 互素。

例1若p1＝7，p2＝3，c＝3，即M(7，3)＝125与M(3，3)＝5，易知二者不互素。p1-p2-1＝3，那么2M(3，1)＋1＝15与M(3，3)＝5也不互素。

若p1＝11，p2＝5，c＝3，即M(11，3)＝2045与M(5，3)＝29，易知二者互素。p1-p2-1＝5，那么2M(5，1)＋1＝63与M(5，3)＝29也互素。

4 伪梅森素数的产生方法

接下来本文将利用等式(1)得到新的伪梅森数的生成方法。在等式(1)中，有：

对于任意素数p1，p2，奇数c，有

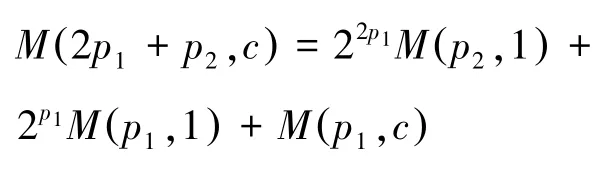
说明：利用等式(1)我们可以通过两个低次的梅森数和一个低次的伪梅森数生成高次伪梅森数。

由于梅森数已有公开的数表，在使用梅森数时可以直接套用数表上的数进行计算。梅森素数表列举如表1所示(以伪梅森素数形式表示)：

表1 前12个梅森素数[1]

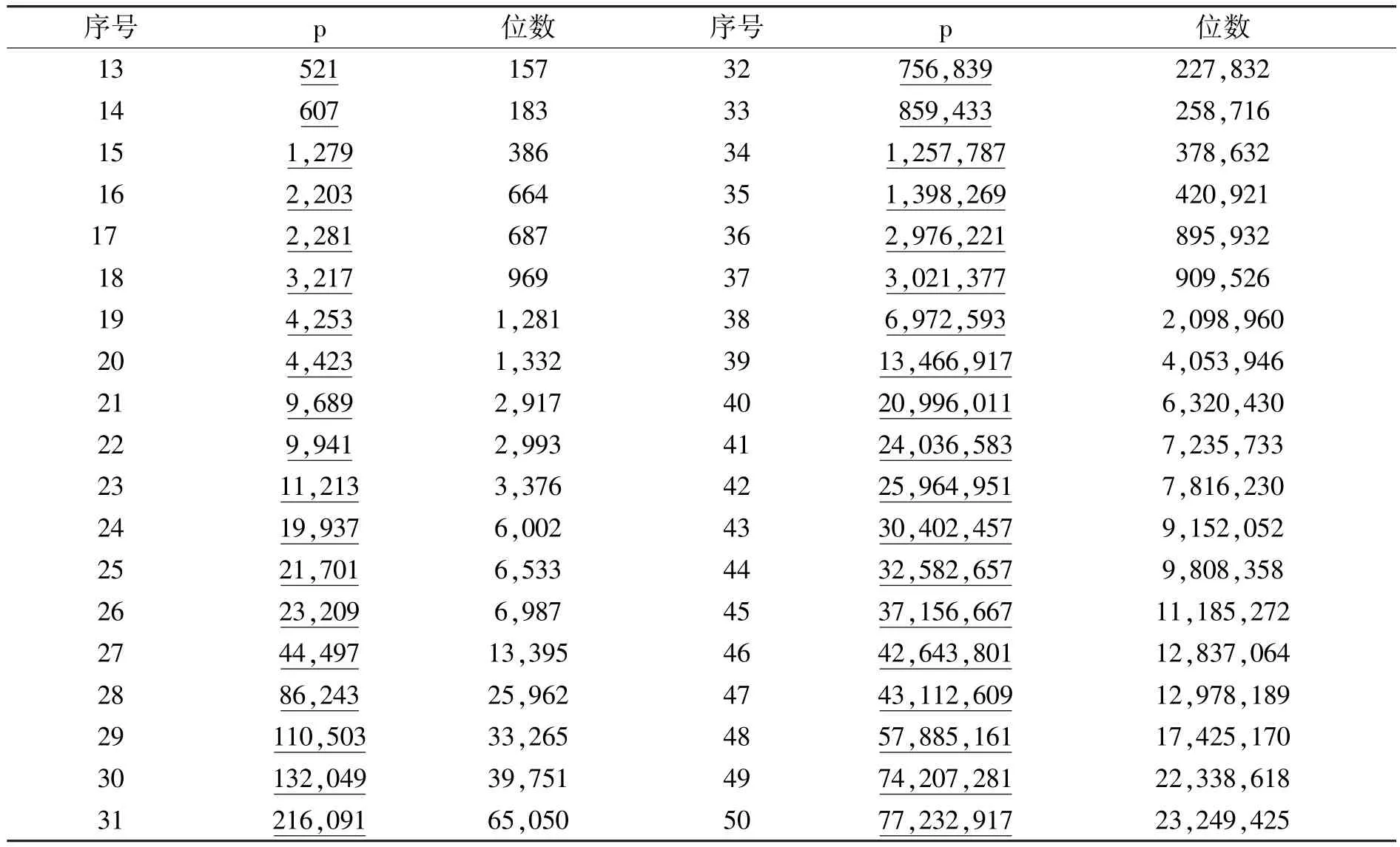
表2 第13至50号梅森素数 [1]

从递归性质出发，根据上述定义可以不断推出新的伪梅森数这个思想在生成素数上具有广泛应用，具体步骤如下：

步骤1固定c＝t不变，依次选择素数p1，p2，其中p1，p2为存在于梅森素数表中，且M(p1，c) 为素数。

步骤2利用等式(1)生成新的伪梅森数。

步骤3对新的伪梅森素数进行素性检验(包括是 Miller-Rabin检验[9]，Lucas-Lehmer检验[8]等(注：Lucas-Lehmer是针对梅森素数的素性检验，当拓展为伪梅森素数时，该检验并不能通过))，通过则将新伪梅森素数加入伪梅森素数表(c＝t)，并回到步骤1。若不通过检验，则抛弃该数，回到步骤1，重新选择p1，p2。

这样便得到一个新的伪梅森素数表族(c＝t)。

我们以伪梅森素数举例说明：

5 性能分析

5.1 复杂度

通过直接生成一个新的伪梅森素数M(p，c)，需要消耗时间复杂度O(2p)，而消耗的空间复杂度为O(1)。 时空分配不合理，当p值较大时很容易造成溢出。

根据递归方法生成素数方法，通过建立数表来增加空间复杂度为O(n2)，但时间复杂度降低为O(22p1)，其中2p1＝p-p2。增加了时空分配的合理性，大大提高了性能。

5.2 效率

使用递归性质寻找伪梅森素数效率比使用普通方法效率提高很多。其中包括执行的时间，执行时间需通过依据编制的程序在计算机上运行时所消耗的时间来度量。由于复杂度的降低，在计算机上的执行时间也大幅降低。

6 应用

6.1 基于伪梅森素数的RSA密钥对的生成

RSA[6]是第一个安全，实用的公钥密码算法，成为了公钥密码的国际标准，目前是应用最广泛的公钥密码体制。RSA密码算法的数学原理来源于欧拉定理，其安全性取决于大整数因子分解不易实现。公钥密码体制在加密和数字签名上应用广泛，不仅安全、易懂，还容易实现。

RSA密钥对的生成，通常需要以下几个步骤：

(1)选取两个大素数p、q；

(2)计算乘积n＝p×q，φ(n)＝(p-1)×(q-1)，其中φ(n)是n的欧拉函数值；

(3)随机数e(1＜e＜φ(n))(不用保密)，必须满足e与φ(n)互素；

(4)通过扩展欧几里得算法计算d，满足d×e≡1modφ(n)(保密)，即d-1≡emodφ(n) ；通常把 (e，n)称为公钥，(d，φ(n))称为私钥，e和d分别称为加密指数和解密指数，在不知道p和q的情况下，很难计算φ(n)，因而就不知道私钥(d，φ(n))。

例4：我们利用在例2和例3生成的伪梅森素数运算说明。

设p＝M(17，9)＝131063，q＝M(29，3)＝536870909，求 d。

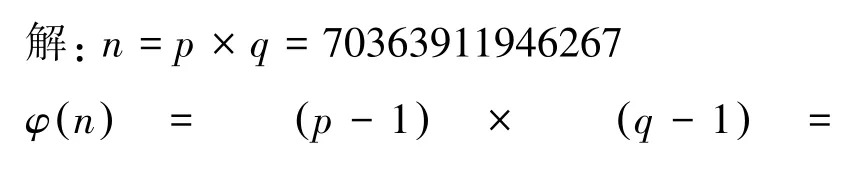
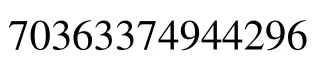
选择公钥 e＝13(素数)，求出d＝924900521。

所以，得到公钥(e，n)＝(13，70363911946267)，私钥为(d，φ(n))＝(924900521，70363374944296)。

由于梅森素数具有2p-1的形式，故容易受到William’sp＋1[10]因式分解攻击。而伪梅森素数以2p-c形式作为因子，从而避免受到William攻击。

6.2 基于伪梅森素数的EIGamal密钥对生成

ElGamal[2]算法，是一种较为常见的加密算法，它是基于1985年提出的公钥密码体制和椭圆曲线加密体系。既能用于数据加密也能用于数字签名，其安全性依赖于计算有限域上离散对数这一难题。在加密过程中，生成的密文长度是明文的两倍，且每次加密后都会在密文中生成一个随机数K，在密码中主要应用离散对数问题的几个性质：求解离散对数(可能)是困难的，而其逆运算指数运算可以应用平方-乘的方法有效地计算。也就是说，在适当的群G中，指数函数是单向函数。

密钥对产生办法如下：首先选择一个素数p，获取一个素数p的一个原根g(若g模p的阶等于φ(p)，则称g为模p的一个原根。(其中φ(p)表示p的欧拉函数，即所有小于等于p的正整数中和p互质的整数的个数))和一个随机数x，且g和x均小于p，计算y＝gx(modp)，则其公钥为y，g和p，私钥是x可由一组用户共享。

ElGamal用于数字签名。被签信息为M，首先选择一个随机数k，k与p-1互质，计算

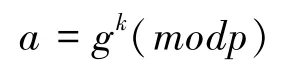
再用扩展 Euclidean算法对下面方程求解b：

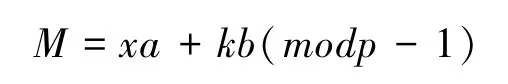
签名就是(a，b)。随机数k须丢弃。

验证时要验证下式：

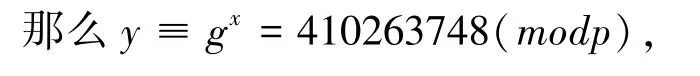
得到公钥(y，g，p)＝(410263748，3，536870909)，私钥为(x)＝(131063)。

6.3 基于伪梅森素数的ECC密钥对生成

椭圆曲线密码学(英语：Elliptic curve cryptography，缩写为ECC)，一种建立公开密钥加密的演算法，基于椭圆曲线数学。椭圆曲线在密码学中的使用是在1985年由Neal Koblitz和Victor Miller分别独立提出的。

ECC的主要优势是在某些情况下它比其他的方法使用更小的密钥——比如RSA加密算法——提供相当的或更高等级的安全。ECC的另一个优势是可以定义群之间的双线性映射，基于Weil对或是Tate对；双线性映射已经在密码学中发现了大量的应用，例如基于身份的加密。

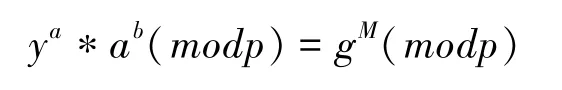
同时一定要检验是否满足1≤a＜p。否则签名容易伪造。

ElGamal用于加密。被加密信息为M，首先选择一个随机数k，k与p-1互质，计算

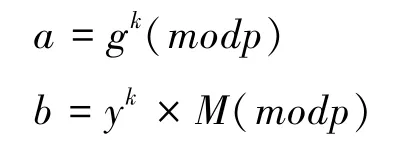
(a，b)为密文，是明文的两倍长。解密时计算

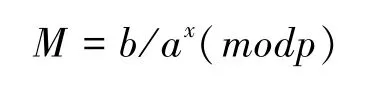
ElGamal签名的安全性依赖于乘法群上的离散对数计算。素数p必须足够大，且p-1至少包含一个大素数。

因子以抵抗Pohlig＆Hellman算法的攻击。M一般都应采用信息的HASH值(如SHA算法)。ElGamal的安全性主要依赖于p和g，若选取不当则签名容易伪造，应保证g对于p-1的大素数因子不可约。

例5：设p＝M(29，3)＝536870909，g＝3是p的一个原根，选择随机数x＝M(17，9)＝131063。不过一个缺点是加密和解密操作的实现比其他机制花费的时间长。

ECC的密钥对产生方法如下：

定义在Fp上的椭圆曲线：

椭圆曲线E(Fp)定义为：

其中O是无穷远点。椭圆曲线E(Fp)上的点数目用＃E(Fp)表示，称为椭圆曲线E(Fp)的阶。

设椭圆曲线参数(p，a，b，G，n)，其中G是基点，n是G的阶。在区间[1，n-1]中随机选取一个整数dB为私钥。计算点QB＝dBG，取点QB为公钥。

加密过程：

(1)用户A将待传输的明文编码到Ep(a，b)上一点M，并产生一个随机整数r。

(2)用户A计算点C1＝M＋rQB；C2＝kG。

(3)用户A将C1、C2传给用户B。

(4)用户B接到信息后，计算C1-kC2-kC2，结果就是点M，再对点M进行解码就可以得到明文。

例6：设p＝M(5，9)＝23，a＝1，b＝1，G＝(3，10)，n＝28

随机数作为私钥dB＝M(17，9)＝9

公钥QB＝(4，21)

6.4 基于伪梅森素数的密钥交换协议

Diffie-Hellman[4]密钥交换协议，缩写为D-H，是一种安全协议。它可以让双方在完全没有对方任何预先信息的条件下通过不安全信道创建起一个密钥。这个密钥可以在后续的通讯中作为对称密钥来加密通讯内容。

例8：首先确定p＝M(29，3)＝536870909，g＝3是p的一个原根。

(1)Alice选择不公开的整数a＝M(17，9)＝131063，然后传送给 BobA＝gamodp，即A＝3131063mod536870909＝410263748；

(2)Bob同样选择一个不公开整数b＝17，然后传送给 AliceB＝gbmodp，即B≡317mod536870909≡387420489；

(3)Alice计算s＝Bamodp，即s＝387420489131063mod536870909＝48621887；

(4)Bob计算s＝Abmodp，即s＝41026374817mod536870909＝48621887；

Alice和Bob就能通过公开信道得到密钥s＝48621887。

7 结论

随着现代密码学的不断发展，素数在信息安全领域以及密码保密领域起到了越来越大的作用，计算机计算能力不断增强，许多依赖于计算量的问题迎刃而解，对于大素数的要求会更高，而伪梅森数是最近所提出的一类拓宽大素数生成的渠道。本文对伪梅森素数进行前瞻性的研究，根据伪梅森素数的定义提出一些相关性质，并根据性质得出递归方法的伪梅森数的生成方法，再基于该性质形成了一系列伪梅森素数族。

对于检验梅森素数的Lucas-Lehmer检验，并不能直接应用于伪梅森素数。我们希望读者在阅读本文后得到启发，推出类似素性检验方法以检验伪梅森素数。