例析构造三角形中 位 线
冯海亮

在初中几何中,有关三角形、四边形的问题中时常会出现线段的中点,在这种情况下,我们可以联想构造三角形中位线,将图形中分散的线段集中起来,从而解决问题。
A.3 B.4 C.2 3 D.32

图1
【解析】如图2,取BC的中点G,连接EG,根据三角形的中位线定理得:EG=4。设CD=x,则EF=BC=2x,证明四边形EGDF是平行四边形,可得DF=EG=4。

图2
【点评】本题考查了平行四边形的判定和性质、三角形中位线定理,通过辅助线构造三角形的中位线是解题关键。
例2 如图3,在△ABC中,用直尺和圆规作AB、AC的垂直平分线,分别交AB、AC于点D、E,连接DE。若BC=10cm,则DE= cm。

图3
【解析】直接利用线段垂直平分线的性质,得出DE是△ABC的中位线,进而得出答案。
解:∵用直尺和圆规作AB、AC的垂直平分线,
∴D为AB的中点,E为AC的中点,
∴DE是△ABC的中位线,
故答案为:5。
【点评】此题主要考查了基本作图以及线段垂直平分线的性质,正确得出DE是△ABC的中位线是解题关键。
例3 如图4,四边形ABCD中,AC平分∠BAD,∠ACD=∠ABC=90°,E、F分别为AC、CD的中点,∠D=α,则∠BEF的度数为 (用含α的式子表示)。

图4
【解析】根据直角三角形的性质得到∠DAC=90°-α,根据角平分线的定义、三角形的外角的性质得到∠CEB=180°-2α,根据三角形中位线定理、平行线的性质得到∠CEF=∠DAC=90°-α,结合图形计算即可。
解:∵∠ACD=90°,∠D=α,
∴∠DAC=90°-α,
∵AC平分∠BAD,
∴∠DAC=∠BAC=90°-α,
∵∠ABC=90°,E是AC的中点,
∴BE=AE=EC,
∴∠EAB=∠EBA=90°-α,
∴∠CEB=180°-2α,
∵E、F分别为AC、CD的中点,
∴EF为△ACD的中位线,
∴EF∥AD,
∴∠CEF=∠DAC=90°-α,
∴∠BEF=180°-2α+90°-α=270°-3α。
故答案为:270°-3α。
【点评】本题考查的是三角形中位线定理、直角三角形的性质、角平分线的定义,掌握三角形的中位线性质是解题的关键。
例4 如图5,在四边形ABCD中,AB=CD,G、H分别是BC、AD的中点,BA、CD的延长线分别交GH的延长线于点E、F,猜想∠AEH与∠DFH的关系,并说明理由。
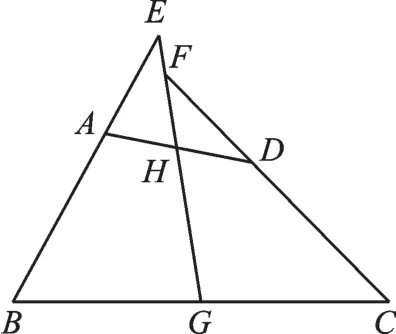
图5
【解析】如图6,连接BD,设BD的中点为M,连接HM、GM。利用三角形中位线,证得△HGM是等腰三角形,则∠MHG=∠MGH。利用三角形中位线定理、平行线的性质推知∠MHG=∠AEH,∠MGH=∠DFH,根据等量代换证得∠AEH=∠DFH。
解:∠AEH=∠DFH。
理由如下:如图6,连接BD,设BD的中点为M,连接HM、GM。

图6
∵点H是AD的中点,
∴∠MHG=∠AEH。
∴∠MGH=∠DFH,
又∵AB=CD,∴GM=HM,
∴∠MHG=∠MGH,∴∠AEH=∠DFH。
【点评】本题主要考查三角形的中位线定理,熟练运用三角形的中位线定理进行线段转换是解题关键,构造合理的辅助线是解题难点。
“有中点,取中点,连中点,造中位线”,这是中点处理常见策略之一。只要你熟练掌握此策略,对于看不见的中位线,也能构造合理的辅助线,任题目变化多端,也能叫它原形毕露!

