数据挖掘技术在高校课程设置中的应用
李晓瑜
(安康学院 电子与信息工程学院, 安康 725000)
0 引言
提高教学质量和学生的学习成绩是高校不断追求的目标,优化课程设置,可以使学生的整体知识系统化,连续化。这样即可以提高学生的成绩还可以提高学生学习的兴趣。通过对学生不同课程成绩进行分析,发现后续开设的课程的成绩受哪一门或哪几门前导课程的影响最大,从而进行课程设置顺序的调整。[1]现有的学生成绩管理系统仅能对数据库中的数据进行存储、查询及简单的统计,对数据进行深入分析的功能还比较欠缺,不利于教学信息的采集,不能够将数据库中有价值的潜在的信息挖掘出来,造成教学资源的极大浪费。数据挖掘技术的出现可以从根本上解决这一问题。[2]
1 数据挖掘
1.1 数据挖掘概述
数据挖掘(data mining)是一种知识发现技术,通过对隐含于数据中的知识进行发现,从而获得有价值的信息,为决策者制定决策提供帮助。[3]一般的数据挖掘基本上分为4个环节:数据准备,数据预处理(ETL),数据挖掘,转换模型或模式评价。[4]数据挖掘常用的方法有集合论法,聚类分析方法,关联规则分析方法和决策树方法等。[5]本文主要使用关联分析方法分析安康学院信息管理与信息系统专业的“数据库原理与应用”,“管理信息系统”和“信息系统分析与设计”3门课程学生成绩之间的关联,通过成绩的关联分析,能够发现学生应该先修哪些课程,后修哪些课程,为该专业学习计划和人才培养方案的制定提供科学依据。
1.2 关联规则
关联规则分析主要是对已知数据中各项之间尚未明确但有价值的关联或依赖关系进行探索,探索规则的确定性及有用性分别借助置信度及支持度予以反映。[6]支持度是某统计数据在数据集合中重要程度的度量,而置信度则是该数据集中可信度的度量。置信度则是用来说明关联规则的强度和可信度,置信度越高,则关联规则越可靠越可信,也就是说符合这条规则的事件发生概率教大。[7]定义事务集T,设X⊆T,Y⊆T且XY=φ,关联规则是形如X⟹Y的蕴含式,规则X⟹Y在T中的支持度用数学公式可以表示为[8]:
Support(X⟹Y)=P(X∪Y)
(1)
支持度表示T中事务X和事务Y同时出现的概率,也就是包含X∪Y事务占总事务的百分比,支持度的值表示X⟹Y在T中出现的普遍程度。当支持度的值大于给定最小支持度的模式称为频繁模式[8]。规则X⟹Y在T中的置信度用数学公式可以表示为[8]:
(2)
置信度表示T中在出现事务X的前提下事务Y出现的概率,表示关联规则的强度[9]。
满足最小支持度阈值(min_support)和最小置信度阈值(min_confidence)的关联规则称为强规则[10]。min_support和min_confidence的取值在百分之0-100之间,应用关联规则进行数据挖掘的目的就是找出事务集中所有的强规则。
1.3 Apriori算法
Apriori算法是经典的关联规则挖掘算法,该算法根据频繁项集的先验知识,应用迭代方法逐层搜索来确定频繁项集[11]。Apriori算法使用逐层搜索的迭代方法:k-项集用于搜索(k+1)-项集。首先,找到频繁1-项集的集合,记作L1,L1用于找到频繁2-项集的集合L2,而L2用于找L3,如此类推,直到不能找到频繁k-项集[11]。Apriori算法的具体步骤可描述如下:
Input: 事务集D,最小支持度阈值min_suppport;
Out: Result={事务数据库中的频繁项集及其支持度}
Result:={ };k:=1;
》C1:=所有的1-项集
While(Ck不空)do
Begin
为每个Ck的项集生成一个计数器Compk[i]:=0;
For (i=1;i≤|D|;i++)
Begin if 第i个记录(TID=i)支持Ck中的第j个k-项集
Then Compk[j]:=Compk[j]+1;
End
Lk:={Ck中满足支持度大于min_support的全体项集}
Lk中频繁项集的支持度保留;
Result: Result∪Lk;
Ck+1:={所有的(k+1)-项集中满足其子集都在Lk中的全体项集}
K=k+1;
End do
2 数据挖掘在课程设置中的应用
2.1 数据选取与预处理
本文样本数据的选取为安康学院信息管理与信息系统专业2013级毕业生的总评成绩,选取信息管理与信息系统专业的4门核心课程,数据库原理与应用,管理信息系统,信息资源管理,信息系统分析与设计,2013级1班的45名同学的成绩作为样本数据,所得到的部分学生成绩分析表如表1所示。
对选取的样本数据进行预处理,处理规则为:成绩大于或等于85 分的字段值设定为“1”,其他成绩设置为“0”;将课程名称分别记为符号K1,K2,K3,K4。对数据进行数据挖掘预处理,结果如表2所示。

表1 信息管理与信息系统2012级成绩分析表

表2 信息管理与信息系统2012级成绩分析预处理表
事务数据库T 中共 45个事务,分别为45个学生四门核心课程的成绩,定义|T|=45,根据Apriori 算法计算事务数据库T中的频繁项集。首先计算第1个频繁项集L1,利用L1×L1的结果数据计算第二个频繁项集L2,…,按照逐层迭代的方式计算出第3个频繁项集L3,将支持度阈值min_support=2其过程如图1所示。
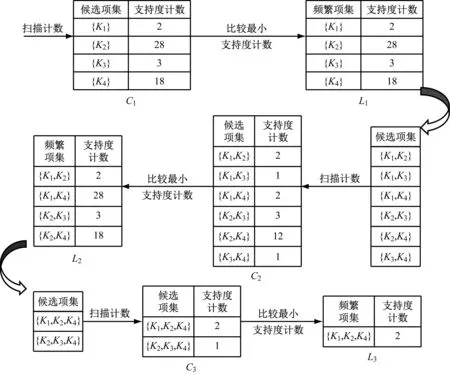
图1 频繁项集生成过程图
2.2 计算置信度
根据上面得到的L3频繁项集{K1,K2,K4},可以得到频繁项集L3的非空子集为{K1,K2},{K1,K4},{K2,K4},{K1},{K2},{K4},参照关联规则基本描述分析,每个L3频繁项集的非空子集的置信度计算结果如表3所示。

表3 置信度计算结果
2.3 关联规则分析结果
由表3中计算出的置信度我们可以得知:
(1)K1和K4同时优秀时,K2也为优秀的可能性为100.0%;
(2)K2和K4同时优秀时,K1也为优秀的可能性为16.7%;
(3)K1和K2同时优秀时,K4也为优秀的可能性为 100.0%;
(4)K2优秀时,K1和K4也为优秀的可能性为7.1%;
(5)K1优秀时,K2和K4也为优秀的可能性为100.0%;
(6)K4优秀时,K1和K2也为优秀的可能性为11.1%。
3 结果分析
将关联规则分析的结果应用于学生具体课程成绩分析,可得出挖掘的信息为:
(1) “数据库原理与应用”课程成绩和“信息系统分析与设计”课程成绩同时优秀时“管理信息系统”课程成绩也为优秀的可能性为 100.0%;
(2) “管理信息系统”课程成绩和“信息系统分析与设计”课程成绩同时优秀时,“数据库原理与应用”课程成绩也为优秀的可能性为 16.7%;
(3) “数据库原理与应用”课程成绩和“管理信息系统”课程成绩同时优秀时,“信息系统分析与设计”课程成绩也为优秀的可能性为 100.0%;
(4) “管理信息系统”课程成绩优秀时,“数据库原理与应用”课程成绩和“信息系统分析与设计”课程成绩也为优秀的可能性为 7.1%;
(5) “数据库原理与应用”课程成绩优秀时,“管理信息系统”课程成绩和“信息系统分析与设计”课程成绩也为优秀的可能性为100.0%;
(6) “信息系统分析与设计”课程成绩优秀时,“数据库原理与应用”课程成绩和“管理信息系统”课程成绩也为优秀的可能性为 11.1%。 由此我们可以得到“数据库原理与应用”,“管理信息系统”和“信息系统分析与设计”3门课程的开设顺序。先开设“数据库原理与应用”,然后开设“信息系统分析与设计”最后开设“管理信息系统”课程这样学生获得优秀成绩的概率最高。应用数据挖掘技术,对不同课程成绩进行分析,根据得到的分析结果对专业课程的设置提供参考,可以优化课程的设置。
4 总结
文章以安康学院电子与工程学院信息管理与信息系统专业为例,介绍了数据挖掘技术在高校课程设置中的应用,通过对挖掘结果分析,发现不同课程间的联系,课程的不同开设顺序对学生的成绩有很大的影响。对学生不同课程的成绩数据进行挖掘分析,发现专业课之间特定的先后关系,可以为专业教学计划的制定提供科学依据。合理的安排课程不仅能提高学生的总体成绩,激发学生的学习兴趣还,提高教学质量,对整个专业的建设有着重要的意义。

