概率的解释谱系及其实践应用——以“机会游戏”为例

程和祥，杨迎莹

（西南政法大学 行政法学院＆监察法学院，重庆 401120）

概率论是一门研究随机现象数量规律的数学学科。第一个有明确文献记载的概率论研究者是意大利的卡尔达诺，他在研究赌博中掷骰子的各种可能情况时提出了概率问题。到了18、19世纪，随着自然科学的发展，学者们注意到某些自然现象和社会现象类似于机会游戏，从而概率论也被尝试应用到自然科学和社会科学中。概率论真正成为一门学科，归功于瑞士数学家雅各布·伯努利，正是他建立了概率论中的第一个极限定理，概率论才正式成为数学的一个分支学科。随后棣莫弗和拉普拉斯又导出了第二个基本极限定理的原始形式，概率论也由此迎来了新的发展阶段。19世纪末，俄国数学家切比雪夫、马尔可夫、李亚普诺夫等人用分析方法建立了大数定律及中心极限定理的一般形式。20世纪初，受物理学的影响，柯尔莫哥洛夫、维纳、马尔可夫、辛钦、莱维及费勒等人开始研究随机过程，取得了一些成果。尽管如此，关于概率的定义，学者们仍众说纷纭。梳理历史上不同学派的观点，可以得到五种概率定义［1］，它们大致可以分为两大类：面向人的认知能力的认识论解释和适用于自然科学或数理科学的客观解释。认识论的概率解释适用于研究人际互动的社会科学，如经济学、法学和社会学等——这些学科刻画了人的认知能力差异；客观的概率解释适用于自然科学，如物理、化学和生物学等——这些学科研究自然界的客观规律。实际上，在实践中运用概率时，我们还需要根据具体情况总结一些经验法则，如概率均等原理、偏态原理和惯性原理。本文将利用2008年中国福利彩票开奖数据，说明这些原理的具体应用。当然，即使如此，我们也还是无法得出必然性的开奖结果；因此，在实际的博彩游戏中，投注仍需讲究策略。

一、 概率的五种解释

（一）概率的古典解释

法国数学家拉普拉斯提出了概率的古典定义，即不进行任何统计试验，仅仅根据演绎法就可事前计算随机事件中各种可能发生的结果及其出现的次数。在古典概率的定义中，有一个假设，即随机事件中各种可能的情况是有限互斥的，并且每个基本事件发生的可能性相等。这个假设其实是值得怀疑的：基本事件的概率真的具有精确的相同的概率值？通俗地说，硬币真的是完美的吗？骰子制造的是均匀的吗？骰子的重心一定位于正中心？轮盘真的不具有倾向性（不会倾向于某一个数字）？对于这种质疑，古典的概率论者提出了“不充分理由原则”：如果没有直接的证据来证明A事件的概率大于B事件的概率，那么可以假定A、B两事件的概率等值。这个辩护同样适用于轮盘赌游戏中的轮盘，也适用于一切赌博游戏中的“赌具”，如扑克牌。显然，“不充分理由原则”确实是不充分的，在实践中应用范围大大受限。

（二）概率的逻辑解释

20世纪20年代，英国著名经济学家凯恩斯出版了《论概率》（1921）一书，对帕斯卡概率做了逻辑解释，建立了第一个概率逻辑系统，后来卡尔纳普等人继续发展了这一理论。该理论假定，对于相同的证据，所有理智正常的成年人都会对某一假说持有相同的置信度。凯恩斯认为：如果h以α的程度部分地衍推a，那么给定h，以α的程度相信a是合理的。因此，概率关系可以刻画合理信念的程度。

在概率的逻辑解释中，凯恩斯与卡尔纳普都采用了无差别原则。由于无差别原则是基于“不充分”理由之上的，因而不可避免地会导致荒谬的结论［2-5］，如酒 - 水悖论［6］和伯特兰悖论［7-8］，为了克服这些悖论，概率的主观解释应运而生。

（三）概率的主观解释

拉姆齐和德·芬内蒂大约在同一时期（20世纪20年代中期）独立地发现了概率的主观理论，即将概率解释为主观置信度。萨维奇在《统计学基础》（1954年）中拓展了这个思想。概率的主观解释通常又称为贝叶斯概率解释，但有些贝叶斯主义者宣称他们的概率解释不仅仅是主观的，不具有客观性，如耶纳斯、杰方斯以及伯格。

概率的主观主义者认为，不同的正常成年个体，尽管都被假定为是理性的，但由于他们的天赋不同以及后天受教育的状况、生活环境和个人运气等因素的影响，他们对浩瀚的宇宙、对复杂社会的认知能力和认知水平并不相同。即使给定同样的证据e，小张和小王对假说h也会有不同的信念度。因而，概率被定义为特定个体的信念度。这不可避免使得初始概率或先验概率具有主观任意性。拉姆齐也承认这种主观任意性，在他看来，先验概率或初始概率只需要满足概率公理即可，而这显然与现实不符合。因为在现实生活中，专家与业余人员的意见和判断显然具有不同的概率。因此，先验概率的随意性遭受了许多的批评。面对批评，德·芬内蒂提出了著名的“意见收敛定理”，为证明意见收敛定理，他又提出了“事件的可换性”，而事件的可换性并不具有说服力，使得德·芬内蒂的观点归于失败。另外，主观主义者在用打赌测量个体信念度时，只讨论了两个主体。然而实际上，目前地球上有70多亿人，仅中国就有13亿～14亿。对于无穷多个主体，主观主义者提出了主体交互解释。

（四）概率的频率解释

19世纪中期，剑桥学派的埃利斯和约翰·文恩提出了概率的频率解释。随后，频率解释被汉斯·莱欣巴赫和冯·米塞斯进一步发展。莱欣巴赫和冯·米塞斯根据极限频率来定义概率：在事件的无穷序列中，某一事件或某一属性出现的相对频率的极限。概率的频率定义，非常适合自然科学领域，因而在自然科学领域中被当作重要的认知工具。但事实上，人的寿命是有限的，人们不能观察到所有事物的极限频率，有些事物的极限频率，人们是无法在有生之年观察到的，人们只能观察到无穷序列中的某一段。另外，单称事件的概率和极限频率的经验确证问题也是频率解释的概率陈述无法解释的。因此，波普尔提出了新的概率解释理论。

（五）概率的倾向解释

1957 年，波普尔发表论文《概率演算与量子论的倾向解释》。在这篇论文中，他提出了概率的倾向解释。随后，他在《科学发现的逻辑》（1959）、《猜想与反驳：科学知识的增长》（1963）和《客观知识：一个进化论的研究》（1972）以及《开放的宇宙》（1982）等一系列著作中，对这一理论进行了详细的阐释和发展。倾向解释认为，概率在某些解释中是一种物理的倾向，这一点与频率的概念是完全不同的。根据波普尔的倾向解释，当相关条件仅仅被重复几次时，我们可以假定概率存在。因而，相较概率的频率解释，波普尔的倾向解释对概率论应用的情形提供了一种在具体的科学实践中可以接受的理论。虽然后期波普尔的单个事例倾向解释面临检验的困难，但吉利斯的长趋势倾向解释能够很好地克服这一困境。

二、 多元主义的概率观：从主观到客观的谱系

总的说来，根据概率解释的多元论观点，不同的解释适合不同的领域，对应于不同的学科。古典解释是适用于机会游戏的，如抛硬币和掷骰子，但对于概率的所有现代应用都不适合；逻辑解释因为无差别原则而面临一些困境；概率的主观解释和主体间解释在社会科学领域是有效的，但显然不适合具有客观性的自然科学——主观解释本身就是用来刻画人的认知差异的，并不描述宇宙的客观性；频率解释适用于经典数学；概率的倾向解释比频率理论能更好地说明自然科学中的概念创新。因此，五种概率解释中，较具有可行性的是主观解释与倾向解释。尽管主体交互解释与主观解释一样都具有一定的局限性，但考虑到现实生活中千千万万个体的认知能力千差万别，因而它们在社会科学中有广泛的应用。目前，人们将概率的主观解释和贝叶斯定理结合起来，对不确定的信息进行推理，这种概率推理系统中最著名的当属朱迪·佩尔于1988年提出的贝叶斯概率网络模型；除此之外，英国南安普顿大学的苏基·芬恩基于贝叶斯概率推理给出了爱情方程式Cr updated（p）=Cr initial（p|e）。在当前可利用的客观解释之中，倾向解释已经替代了频率解释。由于在自然科学中要找到一系列独立的可重复条件是有可能的，因而客观解释在自然科学中有广泛的应用，如当前最热门的大数据推理。

回顾概率论几百年的发展历史，从16世纪的古典概率到20世纪概率的倾向解释，人们对概率的认识构成一个从古典到主观、从主观到客观的解释谱系。古典阶段，人们对随机现象数量规律的认识停留在抽象的可能阶段；逻辑阶段，概率学者基于正常成年人的理性来定义概率；主观阶段，概率学者从现实生活中人的理性认知能力千差万别出发，来讨论一个个具体的概率；客观阶段，人类的思维对象开始向大自然扩展。这样一个从古典到主观，从主观到客观的认识过程，反映了人类对随机现象数量规律的认识不断加深，不断清晰的过程。

三、 实践中的“概率”——以“机会游戏”为例

当我们讨论概率解释的谱系的时候，也提及了每种概率的具体应用领域。但事实上，在实际应用中，上述说明是远远不够的。如20世纪80年代美国电视游戏节目“Let’s Make a Deal”的主持人提出的三门问题，即蒙提·霍尔悖论［9］，并不是用我们上述的概率论知识就能轻易解决的。另外，古典概率当然适用于机会游戏，但显然难以找到一种机会游戏完全符合古典概率。抛掷钱币、骰子和轮盘赌这些当然都属于机会游戏。在这些机会游戏中，投注的技巧和策略是不可缺少的：一是资金要合理分配，不要孤注一掷；二是要定一个“止损点”，到点主动出局。但除此之外，这些机会性游戏又涉及另一个重要概念，即随机数——也就是数字和数字之间毫无关系。真正的随机数是使用物理性随机数发生器产生的，而物理性随机数发生器技术要求比较高。在实际的生产和日常生活中，大多数场合仅仅使用伪随机数就能满足需要。这种伪随机数不是完全随机的数列，而是表现出一定的周期性，但是在统计特征上类似于随机数。伪随机数产生相对简单，通常通过计算机或计算器产生。我们日常生活中的数字型彩票，它的中奖号码就是随机数字生成器产生的［10］。即使不考虑人为（操纵）因素，由于受到各种条件的限制，比如机器的机械性能、机电配合等因素的影响，电脑彩票产生的中奖号码其实是一种伪随机数——尽管它的随机性很强。一方面，由于随机性强，因而试图采用某种算法准确算出每一期的中奖号码是不可能的；另一方面，由于是伪随机数，那么中奖号码不可避免就会表现出一些特征或规律，利用这些规律将中奖号码压缩到一个很小的范围，再采取适当的投注策略，确保盈利是完全可能的。当前的博彩业已经是高科技行业，每一个赌场都拥有较多数学工程师和计算机程序员。现代摇奖机程序的设计，汇集了一系列数学大师的智慧——高斯的概率论、泰勒的级数论和著名的凯利公式都有应用。但是在长期的彩票游戏中，人们根据实际经验，总结出了如下三个实用的结论：

第一，概率均等原理。这里的概率可以理解为频率（在事件的无穷序列中，某一事件或某一属性出现的相对频率的极限），是一种大的整体的趋势与规律；几率，是指在已经发生的随机事件中，某一种随机事件所占的比例，是较少数据统计的结果，表明阶段性的趋势和规律。以前由于技术所限，人们难以获得开奖的历史数据。现在，由于计算机技术和移动互联网技术的发展，人们获得这些数据并不特别困难，甚至轻而易举。

第二，偏态原理。所谓偏态，指的是某个指标未开出的期数与开出期数的百分比。彩票摇奖的开奖号码在长期趋势中表现出来的是随机性，就有限期次来说，在不考虑人为因素的情况下，开奖数据表现的恰恰是一种伪随机性。由于摇奖机的构造、彩球的制作等人们无法确知的因素，使各个备选奖球被摇出的概率在一定时期内表现的并不完全均等，在某个相对短暂的时期内恰恰表现出一种或明或隐的偏态。不管是福利彩票（3D、新3D和双色球以及刮刮乐等），还是体育彩票（排列3、排列5和超级大乐透以及七星彩），我们都能发现这种现象。下文将有实例，此处暂且不表。

第三，惯性原理。由于备选奖球在质量、 形状方面的差异以及彩票摇奖机的固有特性，使某些奖球在短期内中出现的次数多于其他的奖球，从而出现“强者恒强”的情况。

这三大原理是彩民在实际的博彩游戏中，根据经验做出的总结，有极强的实用性。当然，在具体的应用过程中，对三大原理都可作适当修正和延伸。例如，彩民们在中国福利彩票和中国体育彩票中针对数字型和乐透型彩票使用的遗漏分析技术，就是基于概率均等原理和偏态原理。惯性原理本意是指某些奖球在短期内中出现的次数多于其他的奖球，而在博彩实践中，有时候我们需要考虑的不仅仅是一个个奖球，而是奖球和奖球构成的号码组合，考察号码组合之间的依赖关系，最经典的莫过于2008年的案例。在2008年年初，中国福利彩票3D的开奖数据有一些值得研究的现象［11-12］。例如，2008007 期、2008008 期、2008036 期、2008037期、2008043期、2008044期共6期，开奖数据用表1展示如下：

从表1可以看出，号码组合320和号码组合149之间表现出很强的依赖性，且奇迹般地在短时间之内（45天之内）出现三次。

根据概率的古典定义，2008年2月20日开奖号码为149的概率是1/1000；根据概率的频率解释，开奖号码为149的概率依旧很低；而如果我们采用倾向解释，根据上一期的开奖号码320，可以得出下一次开奖号码倾向于149。通过福彩中心的数据，我们可以发现2008年2月20日，不少职业彩民抓住了这次机遇，这一点可以从中奖注数79291注看出来——当期中奖注数明显偏高，返奖比例高达200.18%。出现这种情况的原因，有可能是摇奖机的程序陷入某种死循环，在一系列“天时地利人和”的综合作用下，出现这种巧合。因此，这种情况属于小概率事件，不是必然规律。因此，不能把这种现象当作长期的投注依据，更不能“孤注一掷”。事实上，在整个2008年的359期中，除了刚才讨论的6期，320和149之间再也没有这样相邻出现过。而其他号码组合，也仅仅发生过一例：064与028。具体情况，如表2所示：

表1 2008年1—2月中国福利彩票部分开奖状况

从表2可见，064与028之间的依赖性显然不如320与149，因而看出这种特征的人并不多，中奖注数能很好地说明这一点。

号码组合之间的依赖性只是我们的一种分析方法，在实际的3D博彩游戏中，职业彩民还会从多个角度分析开奖号码的属性，如开奖号码的和值、和尾、跨度、大小、奇偶以及质合等属性。有的彩民还会从试机号入手，也有的彩民采用012路分析方法。总之，在彩票游戏当中，中奖号码的产生是伪随机的，时间一长，这些中奖号码就会形成某种可以预测的模式。因此，在“数字型”彩票游戏当中，我们可以对历年的中奖号码进行分析，从而预测未来趋势，以便正确地估计最有可能在下次开奖中出现的号码。将这种思路贯穿于双色球游戏之中，我们可以得到如下结论：（1）不要选择过去的中奖号码；（2）不要选择6个连续的数字；（3）不要选择属于同一个数字区间的数字；（4）不要选择01-02-03-04-05-06-07型号码组合；（5）不要选择模式化的号码；（6）不要选择倍数型号码；（7）运用智慧和技巧投注，而不是让机器来选择。一句话，我们应该跳出概率解释的框架，从模式的角度来理解。除了这些技术分析外，在真实的博彩游戏中，彩民还需要考虑赔率问题，需要考虑投注的策略。还是以福彩3D为例，它的投注方式就有十三种：“单选”“组选”“1D”“2D”“通选”“和数”“包选”“猜大小”“猜1D”“猜2D”“猜三同”“拖拉机”“猜奇偶”等。因而，彩民，尤其是职业彩民，需要根据自己的经验和博彩技术，选择相应的投注方式，在确保不输的情况下，赢取尽可能多的利润。尤其是时时彩这种高频彩票，策略选择得当，并且技巧高超，有可能在短期内赚取丰厚的利润。概率起源于赌博，因而在人类的一切赌博活动中皆有渗透。例如，在21点和桥牌游戏中，皆有概率论的应用。和博彩业相比，这些活动表现为人与人之间的竞技，因而“概率”也处于不断的运动变化和调整之中。

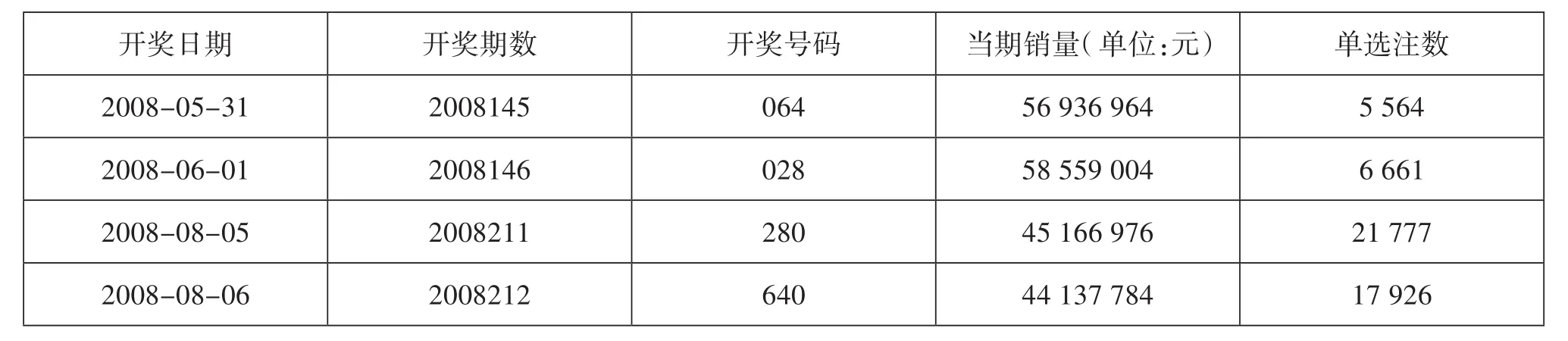
表2 2008年5—8月中国福利彩票部分开奖状况

所有的赌场游戏，从数学上讲，一开始就是对赌徒不公平的游戏。根据大数定律，赌徒下注赌博的次数越多，输的概率越大，破产的概率也越高。因此，进入赌场之前，掌握一定程度的概率知识是十分必要的［13］。因为你不仅仅是在和机器较量，你同时也在和数学家对决——这是一场智力游戏。当然，在中国博彩，你还需要了解中国的国情。正因为这种机会游戏本身的不公平以及中国国情的复杂性，越是发达地区，越是受教育程度高的人群，寄希望于运气的人越少。